PR
絶対値とは？【外し方と絶対値の意味をわかりやすく完全制覇！】
絶対値…この記号は便利なのですが、苦手な生徒が多いです。
「絶対値の方程式や不等式を解く」という技術的な部分に目がいきがちですが、それだとなおさら、
たろぅなんかもう…場合分けとか、±とか、わけわかんない…。
となってしまいます。
この記事では絶対値の意味をもう一度理解しながら、なにをポイントとして押さえるべきかを説明していきます。
目次
絶対値とは
たろぅはぁ…お腹すいたなぁ…でも、今月はお小遣いがあと500円しかない…。あ…はなこさん。
はなこなに？
たろぅ今月ちょっとピンチなんだよぅ！なんでもするから、なんかおごってよ！
はなこいやよ。
たろぅ冷たい！
お願い！お腹が空いて我慢できないんだ！どんな条件でもいいから！
はなこえぇい！しつこい！わかったわよ！
じゃあ、デパートに買い物に行ってきなさい！
（お使いに行った階）×100円分おごってあげるわ！
たろぅなるほど、高い階に上って買い物をこなすほど報酬が上がるシステム！で、何買ってくればいいの？
はなこ私もお腹すいたわ。この500円でドーナツを買っておいで。お釣りは誤魔化すんじゃないよ。必ず領収を貰ってくるのよ。
たろぅ細かい…。とりあえず、行ってきます。
（30分後）
たろぅ買ってきたよ！
はなこはい、じゃあ100円おごって。
たろぅ（聞き間違い？「おごって」？「おごってあげる」の間違いでは？）…ん？
はなこだって、ドーナツは地下一階（ー1)に売ってたでしょ？
たろぅえ？そうだけど…。
はなこじゃあ、
（お使いに行った階）×100円
＝（ー1）×100円=ー100円
でしょ？おごりなさいよ。
たろぅいやいやいや…。え？
はなこあれ？約束を破るのかな？私間違ったこと言ってます？確かに（お使いに行った階）×100円って言って、あなたはそれに合意しましたよね？
たろぅ…。
ということで、絶対値です。
今回のたろう君の敗因（？）は、「階」と聞いて、単純に上に上がるほど沢山おごってもらえる、と思ったところですね。
はなこ「階」って言っただけよ。「ー（マイナス）」だって有り得るじゃない。
たろぅいや…でも１階下がっても１階上がっても手間は一緒じゃない…。下か上かの違いでしょ？
ということで、この「ー（マイナス）も有り得る」けど、「その値を＋」で考えた方が都合いいよね、というのが絶対値です。
せんせそれでは詳しく見ていきましょう。
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
絶対値とは？その本質的な意味と捉え方
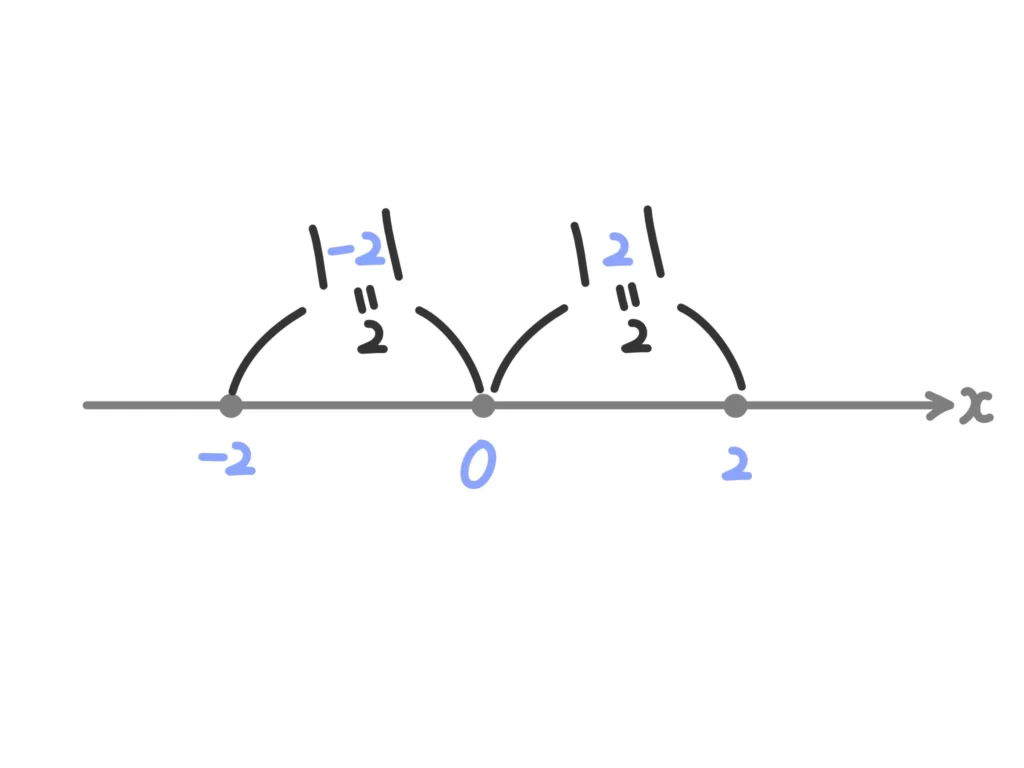
絶対値の意味は「原点からその座標までの距離」です。
たろぅ…なんでいきなり原点が出てくるの？
と思うかもしれませんが、これは、絶対値の中身が、座標など、いわゆる「ー（マイナス）も有り得る値」を想定しているからです。
この感覚は実は複素数平面でも使うので、一応押さえておいてください。
あわせて読みたい
複素数平面(ガウス平面)とは？何が役に立つの？基本を丁寧に説明
２０２２年度高校入学生から新教育課程になりますが、今までの「数学B」は内容をおよそ１.５倍〜２倍に膨らませた形で「数学B」と「数学C」の２科目に別れて勉強するこ…
ですが、絶対値方程式や関数に絶対値がついている場合など、実際に「原点からその座標までの距離」と捉えるケースは少ないです。
絶対値の役割は「中身の符号が＋だろうがー（マイナス）だろうが、＋の値に変換する」というものです。
せんせ「原点からその座標までの距離」と言っているのは、そういう言い方じゃないと「中身の符号に関係なく、その値を＋に変換する」という機能を表現できないからですね。もちろん、実際に原点からの距離、という意味もあります。
ということで、絶対値は
- 原点からその座標までの距離
- 中身の符号に関係なく、その値を＋に変換する
という感覚を持っておいてください。
そして、重要なのは、
「中身は＋、ー（マイナス）、どんな符号でも取り得る」
「絶対値がついた結果は＋の値となる」
という絶対値の中身と絶対値の結果の区別をしっかりとすることです。
せんせ中身は＋でもー（マイナス）でもOK、絶対値の結果は必ず＋（0も含む）になる…。特にこの中身の＋、ー（マイナス）を意識するのが重要ですね。
絶対値の何が嬉しい？
方程式や関数にくっついている厄介者（？）の絶対値…ですが、
中身が＋だろうがー（マイナス）だろうが、＋の値にしてしまう、という特性が便利なときもあります。
一番恩恵を受けやすいのは、座標平面上や数直線上で距離や面積を求めるときです。
例えば数直線上で座標\(a\)の点A、座標\(b\)の点Bがあったとします。このとき、ABの長さは\( |b-a| \)で計算することができます。
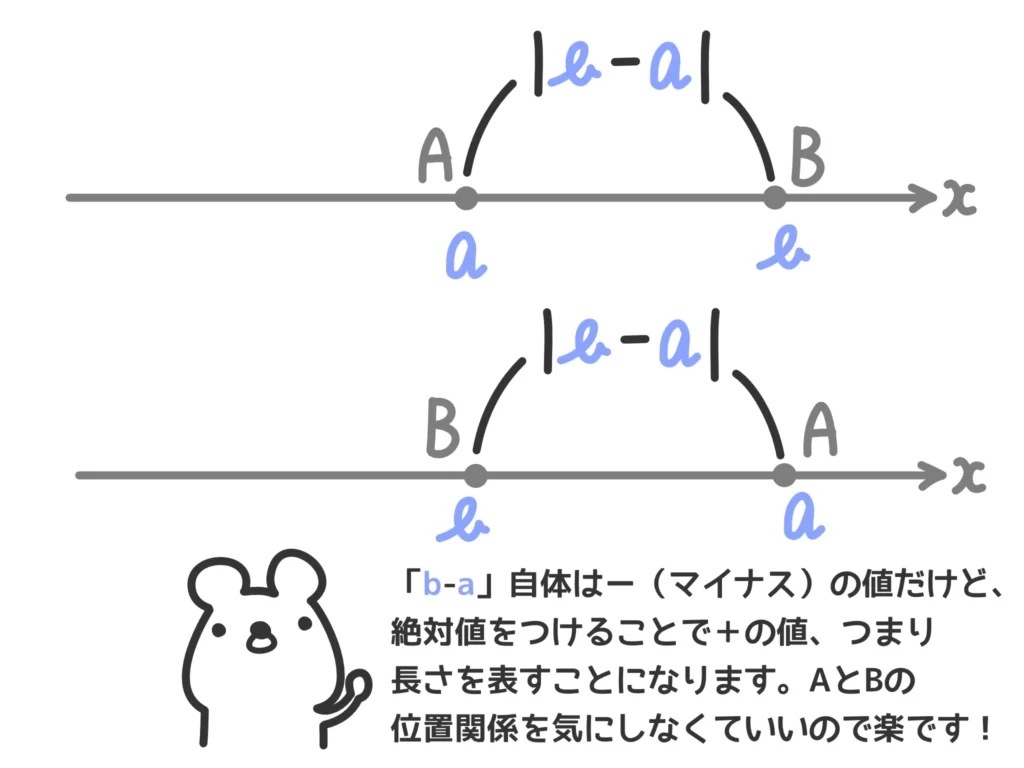
絶対値を使わなければ「(i)\(a > b\)のとき」「(ii)\(b < a\)のとき」に場合分けしなければならないので記述も面倒です。絶対値を使えば\(a\)、\(b\)の大きさに関係なく、\( |b-a| \)と一発でスッキリと表現することができます。もちろん\( |a-b| \)でもOKです。
せんせその他、数学IIで習う「点と直線の距離」や「座標平面上で３点が与えられたときの三角形の面積公式」などでも絶対値を使います。「＋か？ー（マイナス）か？」は本質的には向きが違うだけなので、向きに関係なく距離がほしいときとかには便利です。
絶対値の外し方「場合分けする」
絶対値をつければ「中身の＋、ー（マイナス）に関わらず＋となる」ので、書き方としてはスッキリします。
とはいえ、絶対値があるままでは、実際に方程式を解いたり関数のグラフをかいたりできません。
ですので、絶対値は外すのが基本です。
せんせ外す、というより中身について検証する、というイメージですね。
絶対値は中身の正負で場合分け
絶対値の外し方の基本は「場合分け」です。
場合分けの基準は「中身」です。「中身」の＋、ー（マイナス）で場合分けをします。
絶対値は「中身の＋、ー（マイナス）に関わらず＋とする」のですが、中身が具体的な数字ならともかく、記号や変数であると「＋にする」という操作が上手くできません。
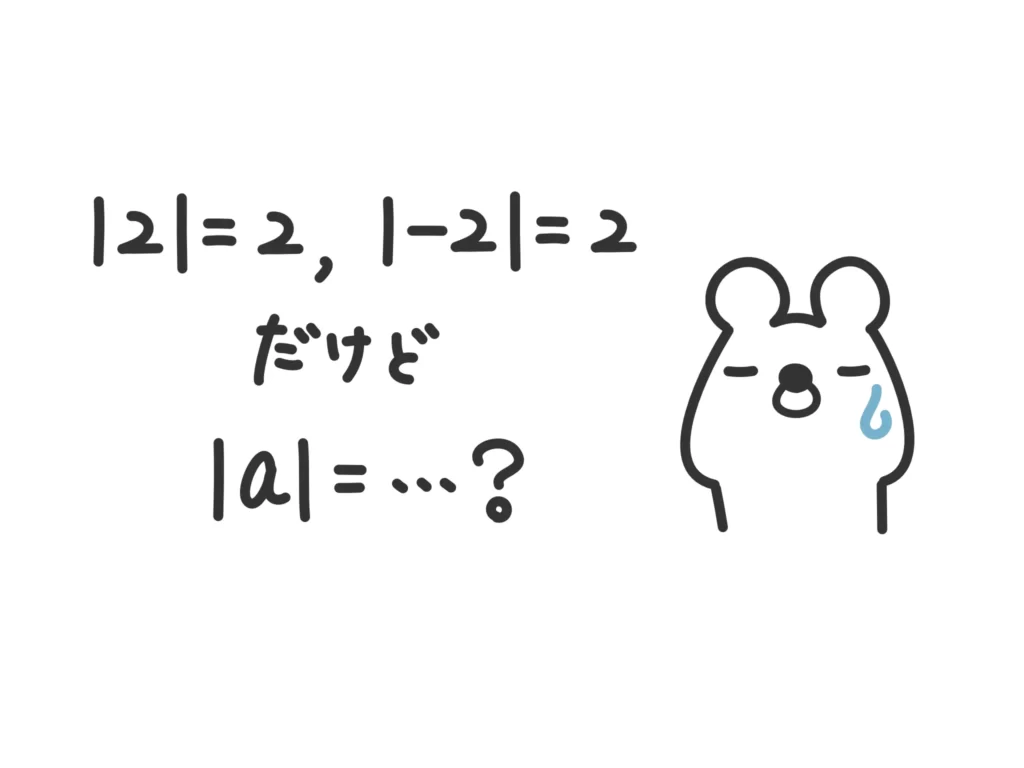
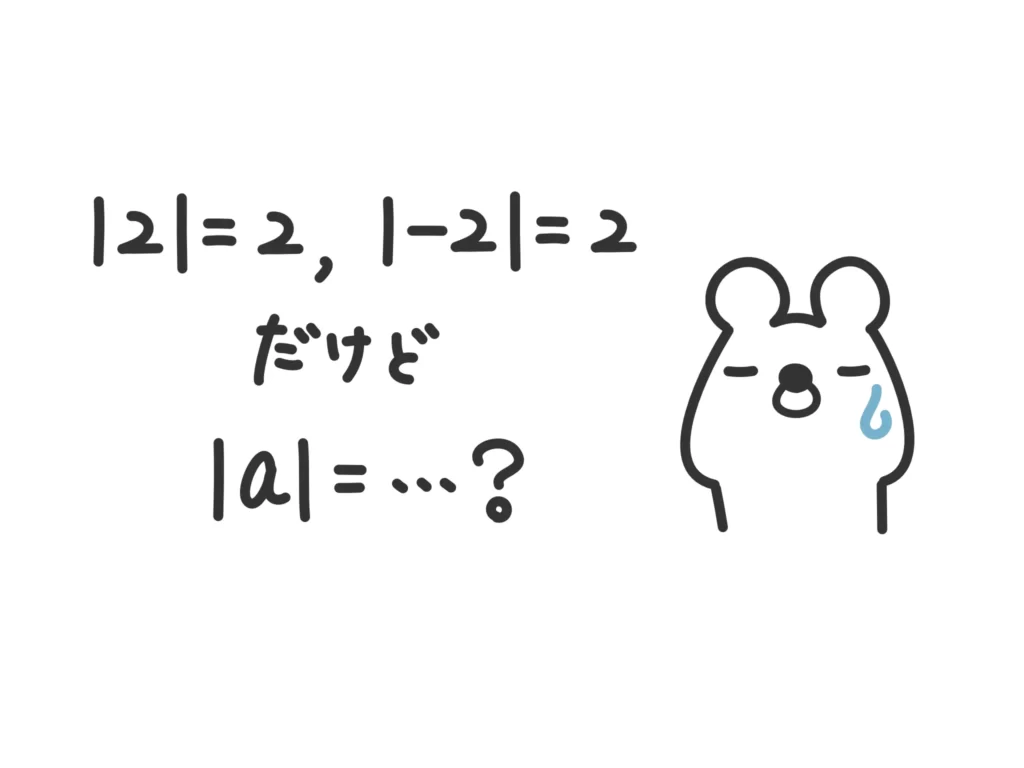
では、具体的にどうするか、というと中身が＋のときはそのまま絶対値を外す、中身がー（マイナス）のときはー（マイナス）をつけて外します。
せんせー（マイナス）の値（や式）にー（マイナス）を逆につけることで、＋にしてしまおう、ということですね！
絶対値の外し方（場合分け）
\( |x| = \begin{cases} x \quad (x \geq 0) \\ -x \quad (x < 0)\end{cases}\)
せんせ\(\geq\)の「＝」はどちらにつけてもいいですが、まぁ普通\(\geq\)につけますね。
例．\(x\)に関する方程式\( |x+1| = 2\)を解け。
中身が＋（0以上）なのか？ー（マイナス）なのか？によって場合分けをします。
せんせあくまで「中身」の正負による場合分けです！
（解答）
（i）\(x + 1 \geq 0\)つまり、\(x \geq -1\)のとき
\( x + 1 = 2\)
\(x = 1\)（これは\(x \geq -1\)を満たす）
（ii）\(x + 1 < 0\)つまり、\(x < -1\)のとき
\( -(x + 1) = 2\)
\(x = -3\)（これは\(x < -1\)を満たす）
（i）（ii）より\(x = -3, 1\)…（答）
絶対値の外し方「二乗する」
実数は＋だろうがー（マイナス）だろうが、二乗すれば＋になります。
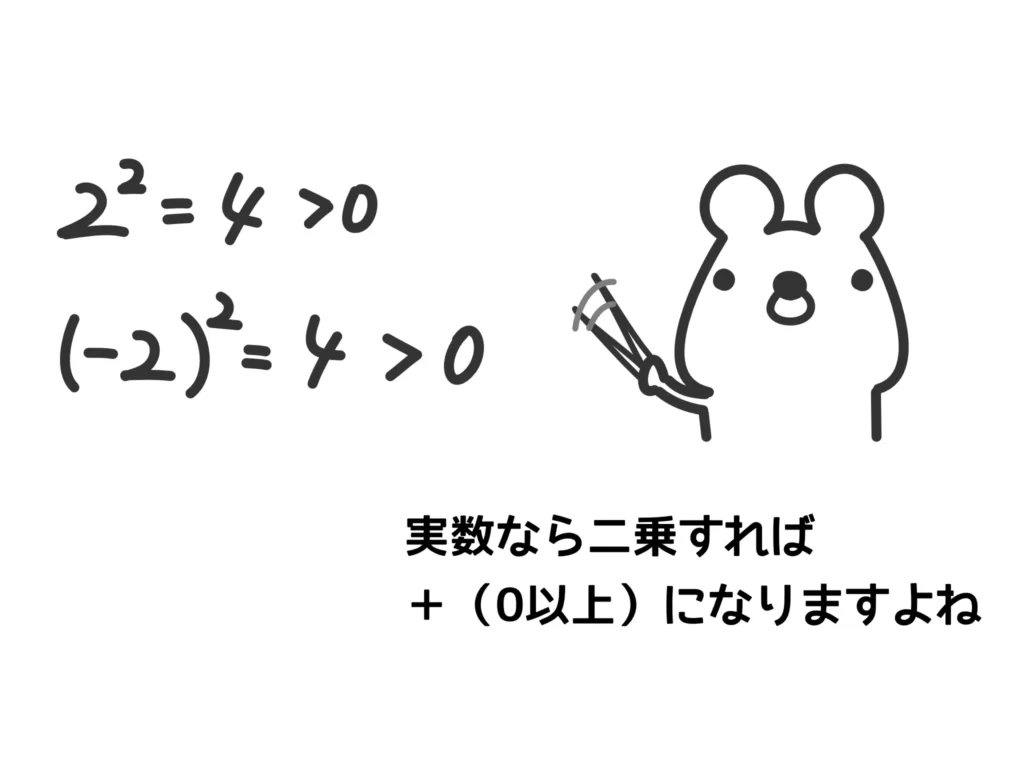
この性質は絶対値に似ていますよね。
ということで、絶対値も二乗してしまえば、外すことができます。
絶対値の外し方（二乗する）
\( |x|^2 = x^2\)
せんせ二乗したら必ず＋になるので、
（絶対値を二乗した値）＝（中身を二乗した値）
としてもOKですよね。
例．\(x\)に関する方程式\( |x+1| = 2\)を解け。
さきほどと同じ問題ですが、二乗して解いてみます。
（解答）
\( |x+1|^2 = 2^2\)
\( (x+1)^2 = 2^2\)
\( x^2+2x-3=0\)
\( (x+3)(x-1) = 0\)
\( x = -3, 1\)…（答）
ただし、二乗すると式が複雑になるのがデメリットです。問題によっては解けなくなる程複雑になります。
せんせその上、細かいことを言うと（実は結構な問題だけど）、二乗すると同値性が崩れるのが問題です。
なので、あまりむやみに二乗するのはオススメできません。上手く解けない場合もあるんです。
練習問題1-3【No.11】
次の\(x\)に関する方程式を解け。
(1) \( |x+1| = x \)
(2) \( |x(x+1)| = 3x \)
答え
(1) 解なし
(2) \(x = 0, 2\)
練習問題の模範解答も販売中！
１分野２００円なので、解答が欲しい分野だけ格安で購入できます！！
別解や思考方法、注意点、補足説明など、note記事だからできる、他にはなかなか無い模範解答に仕上がっています。
絶対値のまとめ
絶対値の基本事項の確認でした。
絶対値方程式・不等式を解く練習をしていると、絶対値の基本がなんとなくゴチャゴチャになってきます。
- 中身は＋、ー（マイナス）どちらも取り得る。絶対値を外す場合は中身の＋、ー（マイナス）で場合分けをするのが基本。とにかく「中身」を意識するのがポイント。
- 絶対値の結果は必ず＋（0以上）になる。
せんせ絶対値が出てきたら、この２点は常に意識しておきましょう。
ちょっと一息
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
また、このブログで活躍してるクマのLINEスタンプも販売しています！ぜひ一度見てみてください！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
