PR
ベクトルの分解?一次結合?超重要な「ベクトルの一意性」とは?
ベクトルは便利で重要な考え方ですが、苦手な人が多い分野でもあります。
原因は「イメージ」と「その場での思考」が重要だからです。
 たろぅ
たろぅその状況に応じた対応って苦手…。
ですが、その分覚えることも少ないですし、基本的なイメージをしっかりと掴むことができればあとはちょっと練習するだけでベクトルの理解はかなり深まります。



要は最初の本質部分が大事!
「ベクトルは感覚だ!」
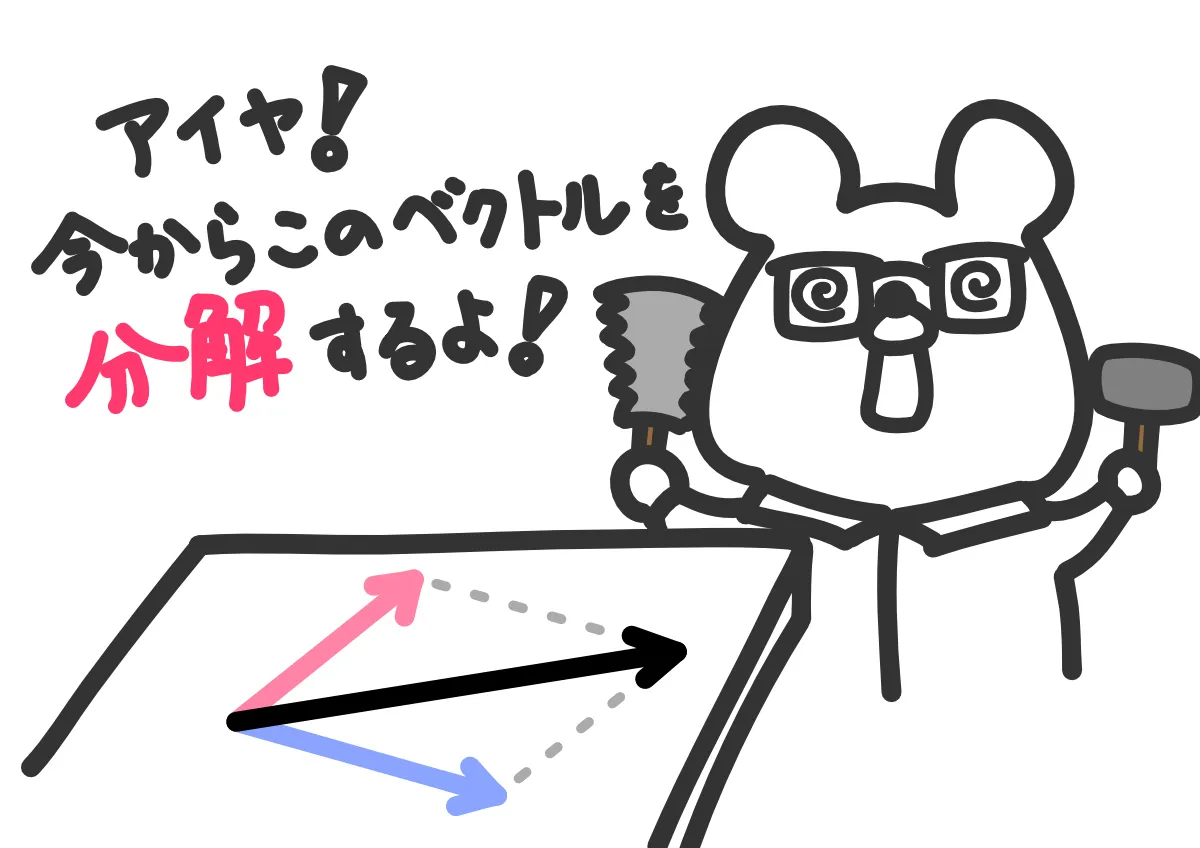
この記事では「ベクトルの分解」や「ベクトルの一次結合」など、色々な言い方をされる「任意のベクトルは一次独立なベクトルの和でただ一通りに表される」ことについて説明していきます。



…いきなり何言ってるか意味不明。難しい漢字使いすぎだろ。
…文字に起こすとイヤになりますが、図を用いながらなるべくわかりやすく説明していきます。ベクトルは感覚です。
ベクトルの分解(一次結合)と表されるアレってなに?
ということで、今回は茶番なし、図を多用、「ベクトルの分解」「ベクトルの一次結合」と言われるアレについて正しい感覚を身につけてもらいたいと思います。



一応分解の一意性について、言葉で説明するとこんな感じです。
\(\overrightarrow{a} \neq \overrightarrow{0}\)、\(\overrightarrow{b}\neq \overrightarrow{0}\)かつ\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行でないとき、
平面上の任意のベクトル\(\overrightarrow{p}\)は、
\(\overrightarrow{p} = k \overrightarrow{a} + l \overrightarrow{b}\)
の形にただ1通りに表される。(ただし、\(k\)、\(l\)は実数である)



…帰る。
…まぁ意味わかりませんよね。図を使って何を言っているのか、丁寧に説明していきましょう。
ベクトルの分解「任意のベクトルp」について
まず最初のポイントは「任意のベクトル\(\overrightarrow{p}\)」というところです。
任意の…つまり、どんなベクトル\(\overrightarrow{p}\)でもいいよ、ってことです。

ベクトルの分解「ka+lb」について
ここが最大のポイントです。
「\(\overrightarrow{a} \neq \overrightarrow{0}\)、\(\overrightarrow{b}\neq \overrightarrow{0}\)かつ\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行でない」という条件の\(\overrightarrow{a}\)と\(\overrightarrow{b}\)を使って、
「どんなベクトル\(\overrightarrow{p}\)でも、
\(\overrightarrow{p} = k \overrightarrow{a} + l \overrightarrow{b}\)…(※)
という感じで(平面なら)2つのベクトルの和の形で表せるよ」
ということです。
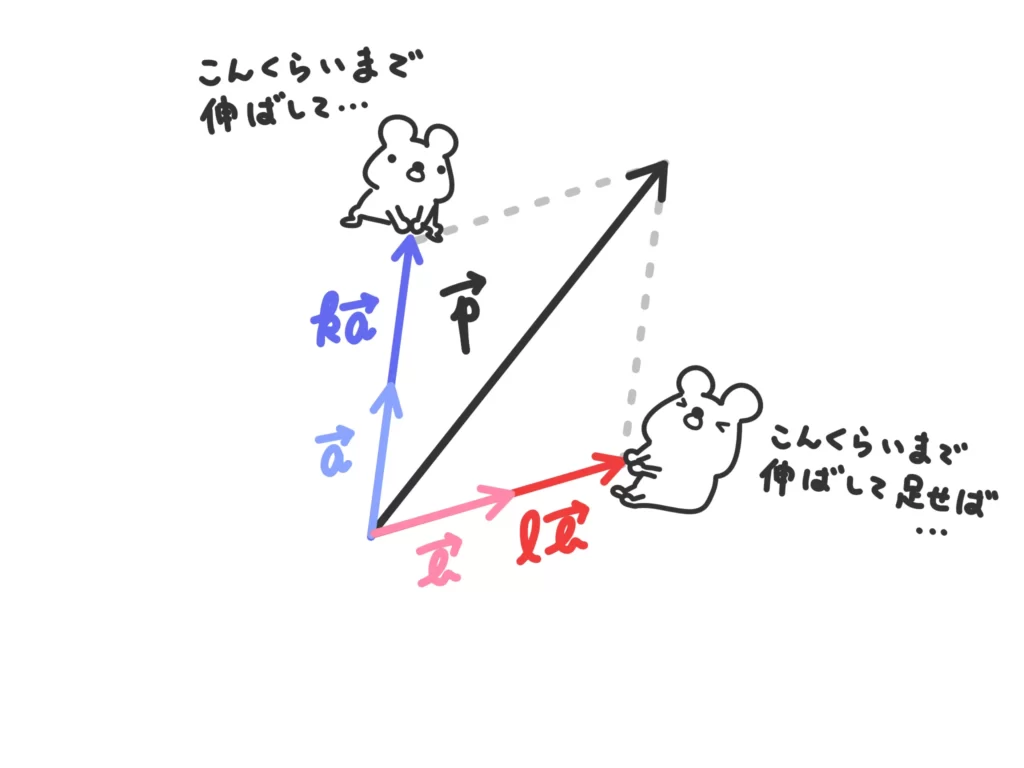
もう少し(※)のところを噛み砕いて言うと、
\(\overrightarrow{a}\)を適切に伸ばして(or縮める、逆方向に伸ばす)、\(\overrightarrow{b}\)も適切に伸ばして足すことでどんなベクトル\(\overrightarrow{p}\)でも表せるよ、ということです。

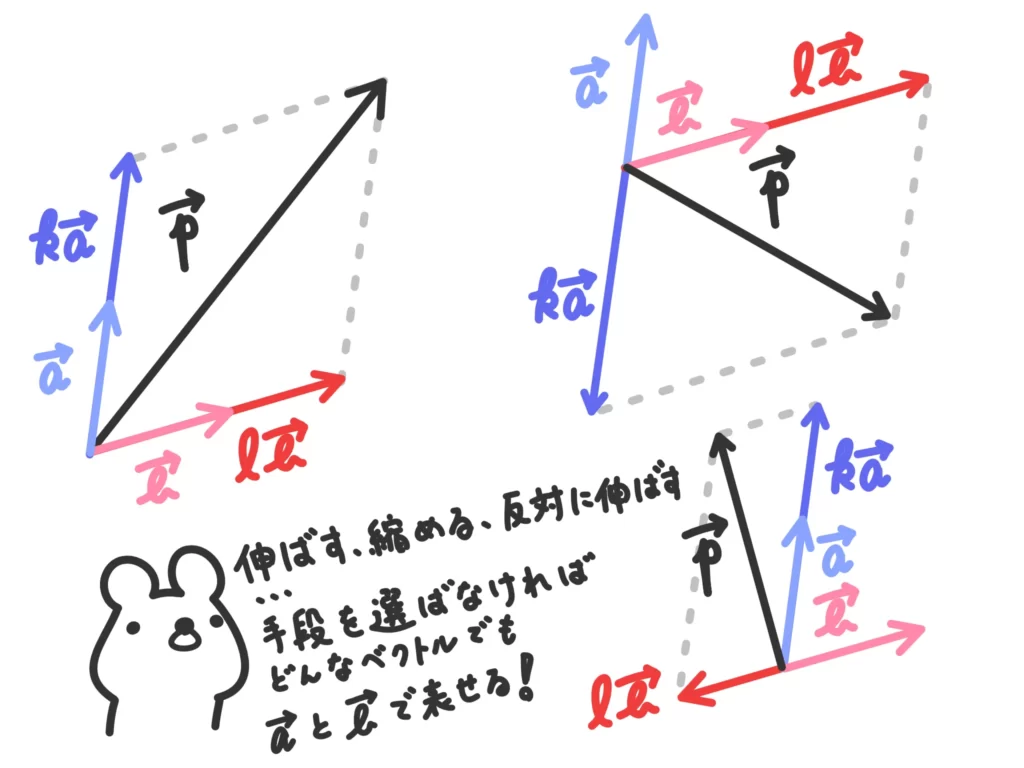




はぁ…なるほど。そういうこと。…で?
「言われてみればそうだよね」と思うかもしれませんが、このベクトルの分解(一次結合)で主張したいことを説明していきます。
主張したいこと1.平面のベクトルは一次独立な2つのベクトルで表せる
2次元という言葉があるように、
平面上にあるどんなベクトルでも、
2つのベクトル\(\overrightarrow{a}\)と\(\overrightarrow{b}\)を使って表せるよ、
というのが主張したいことの1つ目です。
しかも、この2つのベクトルはどんなベクトルでもOKです!
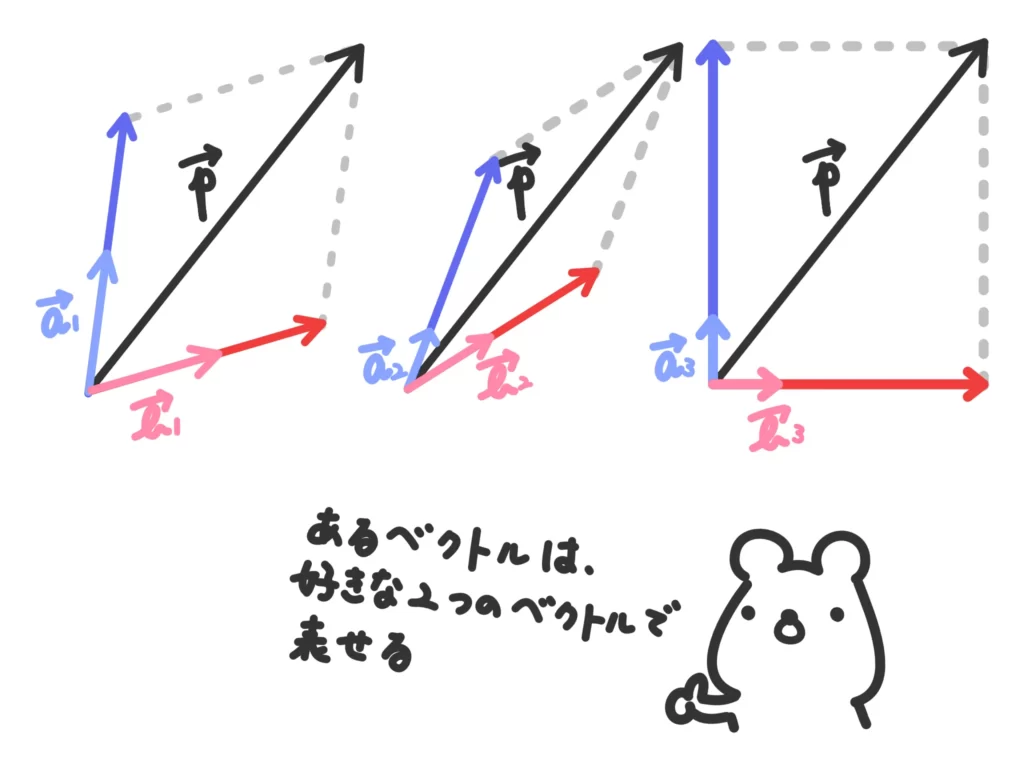

この2つのベクトルを基底ベクトル、と言います。



基底ベクトルは問題や設定によって異なります。その基底ベクトルで平面上の全てのベクトルを表すことができる、という感覚ですね。
ベクトルの一次独立
「どんなベクトルでもOK!」と言いましたが、半分ウソです。
この2つのベクトルは「\(\overrightarrow{a} \neq \overrightarrow{0}\)、\(\overrightarrow{b}\neq \overrightarrow{0}\)かつ\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行でない」という条件を満たしていなければいけません。
この条件を一次独立といいます。
\(\overrightarrow{a} \neq \overrightarrow{0}\)、\(\overrightarrow{b}\neq \overrightarrow{0}\)というのはわかりやすいですが、「\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行でない」という条件が重要です。



まぁ、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が平行だったらどうなるか、やってみればわかります。
次の図を見てください。
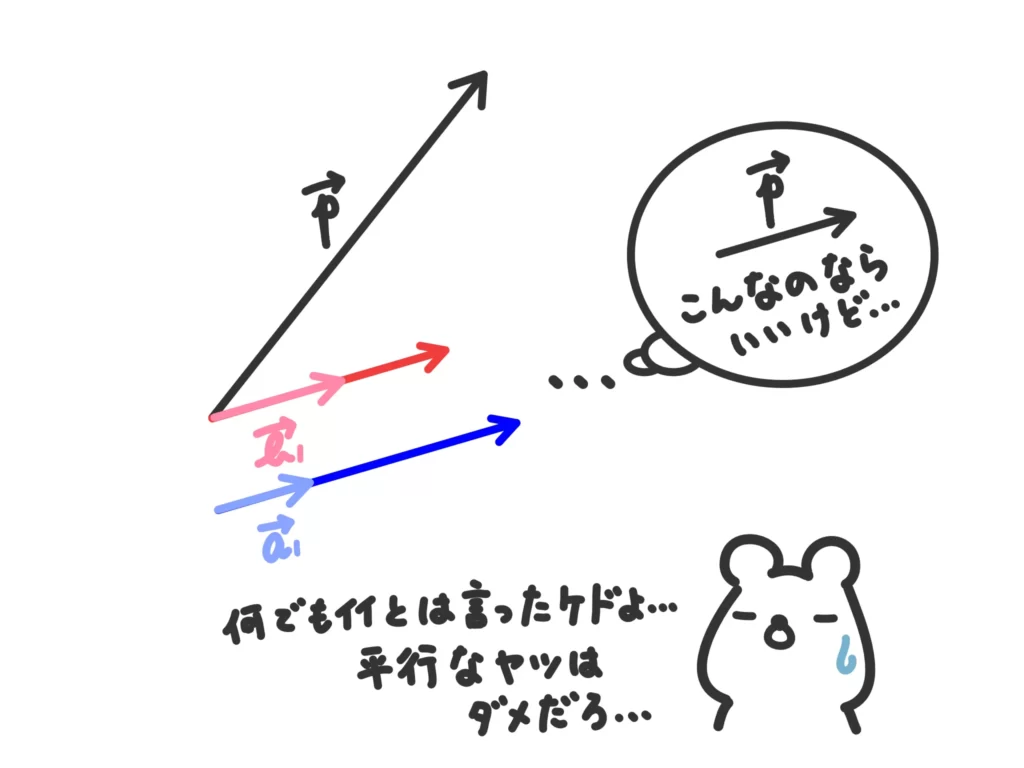

この図を見たらわかると思いますが、2つのベクトルが平行だとその方向のベクトルしか表すことができません。



平行でないベクトルを2つ準備することで、初めて平面上の全てのベクトルを表すことができるのか…。
主張したいこと2.ベクトルの和の表し方はただ一通りである
\( \overrightarrow{p}\)を\( \overrightarrow{a} \)と\( \overrightarrow{b}\)の和で表した、
\(\overrightarrow{p} = k \overrightarrow{a} + l \overrightarrow{b}\)
この形は、ただ一通りに決まり、それ以外の表し方はない、ということです。
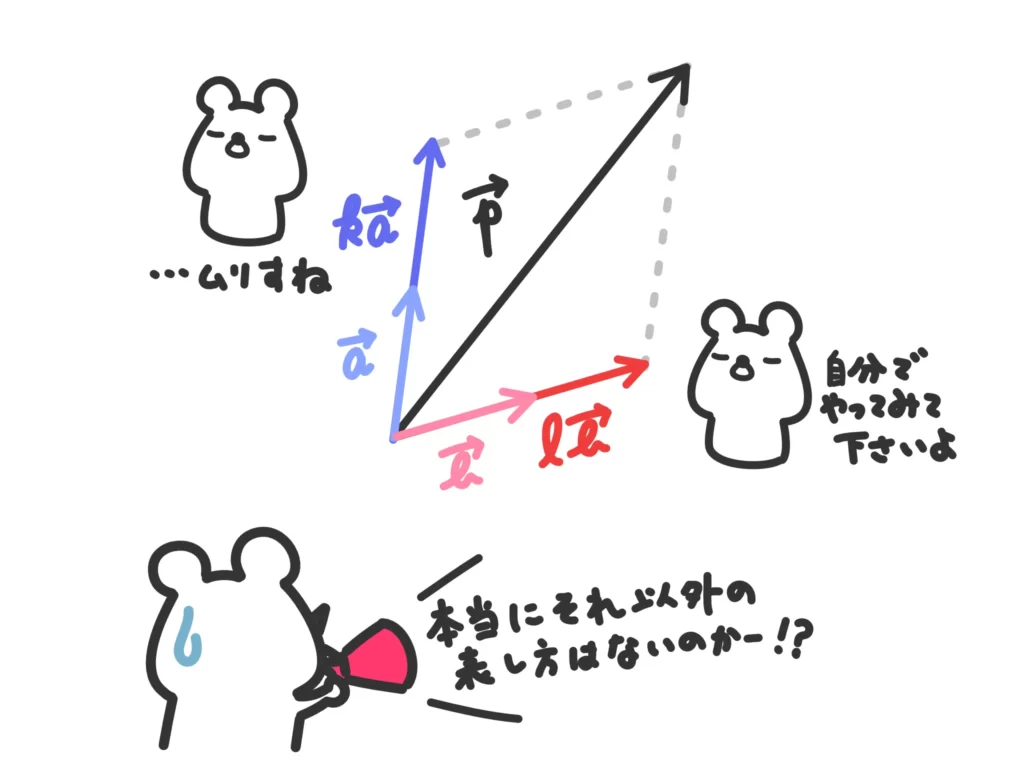




(だからなんだ…)
と思うかもしれませんが、この後「交点の位置ベクトル」という問題で、\(\overrightarrow{p}\)を
\(\overrightarrow{p} = k \overrightarrow{a} + l \overrightarrow{b}\)
と表した上で、別の変数\(m\)、\(n\)を使ってもう一通り、
\(\overrightarrow{p} = m \overrightarrow{a} + n \overrightarrow{b}\)
と表せたとすると、この「ただ一通りでしか表せない」という性質から、
\(k=m\)かつ\(l = n\)
となります。これを利用して解く問題が出てきます。



具体的な問題を解くときには4つも文字は使わないんですがね…。
こういう問題が出るんだ、と思ってもらえればOKです。
まとめ
ベクトルの分解、といわれる性質について説明しました。
ベクトルの分解は「わかりにくい…」か「…それで?」となりがちな部分です。
基本的な部分なのですが、今後実際に問題を解く際にも使う性質なので、とりあえず「なるほど」程度には理解しておいてください。