PR
中間値の定理とは?【証明から注意点、実際の使い方について】

中間値の定理は数学Ⅲで習うのですが、意味を理解することは数学Ⅲを習っていなくでも可能です。
この記事では、中間値の定理の証明から注意点、練習問題について説明していきます。
中間値の定理とは?証明も!
 たろぅ
たろぅはなこさん!見て!すっげぇ!さっきの大雨でグラウンドが全面水浸しだ!こんなの見たことねぇぜ!



…あんた、浮かれてるけど、いいの?



ん?なにが?



だって、あんた昼休み、先生に「放課後、この大量のボールをグラウンド向こうの倉庫に持って行っとけ」って言われてたじゃない。



…。


ということで中間値の定理です。
グラウンドの手前から向こうに渡ると、どこかで必ずグラウンド(に溜まった水たまり)を横切ることになります。当たり前ですね。



…ま、中間値の定理というのはそういうことです。
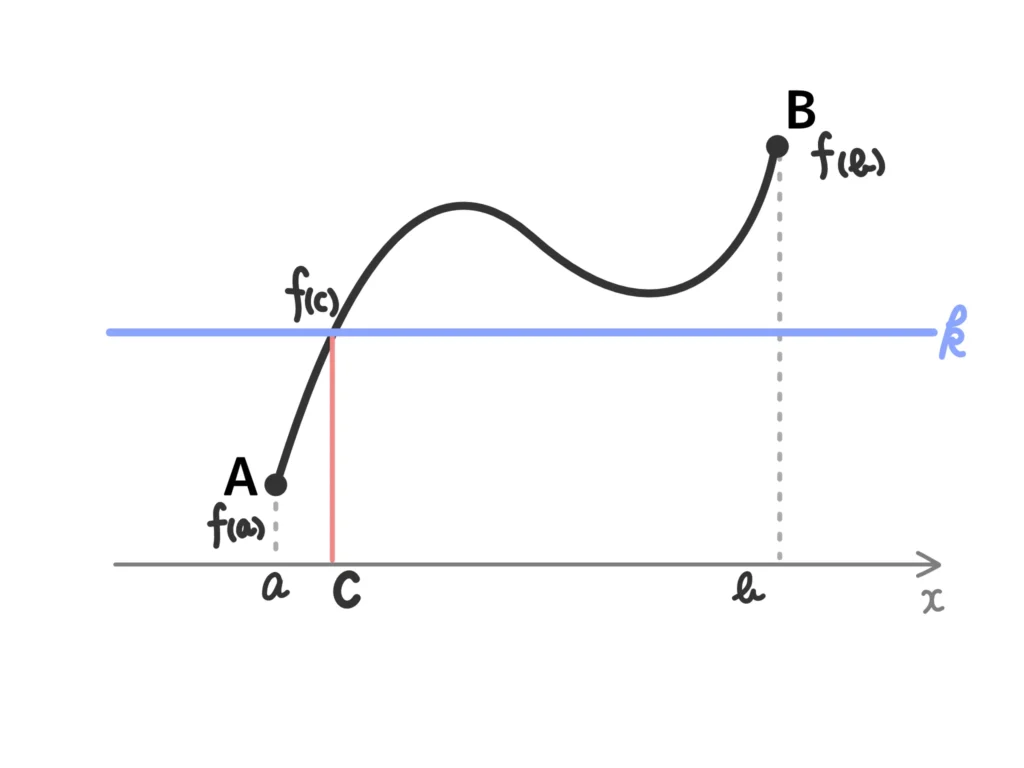
中間値の定理
関数\(f(x)\)が閉区間\([a,b]\)で連続で、\( f(a) \neq f(b)\)ならば、\(f(a)\)と\(f(b)\)の間の任意の値\(k\)に対して、
\(f(c)=k\)
となる実数\(c\)が、\(a\)と\(b\)の間に少なくとも1つ存在する。

証明



まぁまぁハードですが、面白いといえば面白いです。
いくつか証明方法がありますが、個人的に面白いと思う区間縮小法で証明してみましょう。(特に区間縮小法という名前にこだわる必要はありません、「こんなやり方があるんだなぁ」程度でOKです。)
(証明)
まず、\(f(a) < k < f(b)\)として考えます。(\(f(a)> k > f(b)\)でも同じように証明できます。)
次に、数列\(\{a_n\}\)、\(\{b_n\}\)を次のように定めます。
① \(a_1 = a\)、\(b_1 = b\)
② \(\displaystyle f \left( \frac{a_n + b_n}{2} \right) \leq k\)のとき
\(\begin{cases} \displaystyle a_{n+1} = \frac{a_n + b_n}{2} \\ b_{n+1} = b_n \end{cases}\)
\(\displaystyle f \left( \frac{a_n + b_n}{2} \right) > k\)のとき
\(\begin{cases} a_{n+1} = a_n \\ \displaystyle b_{n+1} = \frac{a_n + b_n}{2} \\ \end{cases}\)
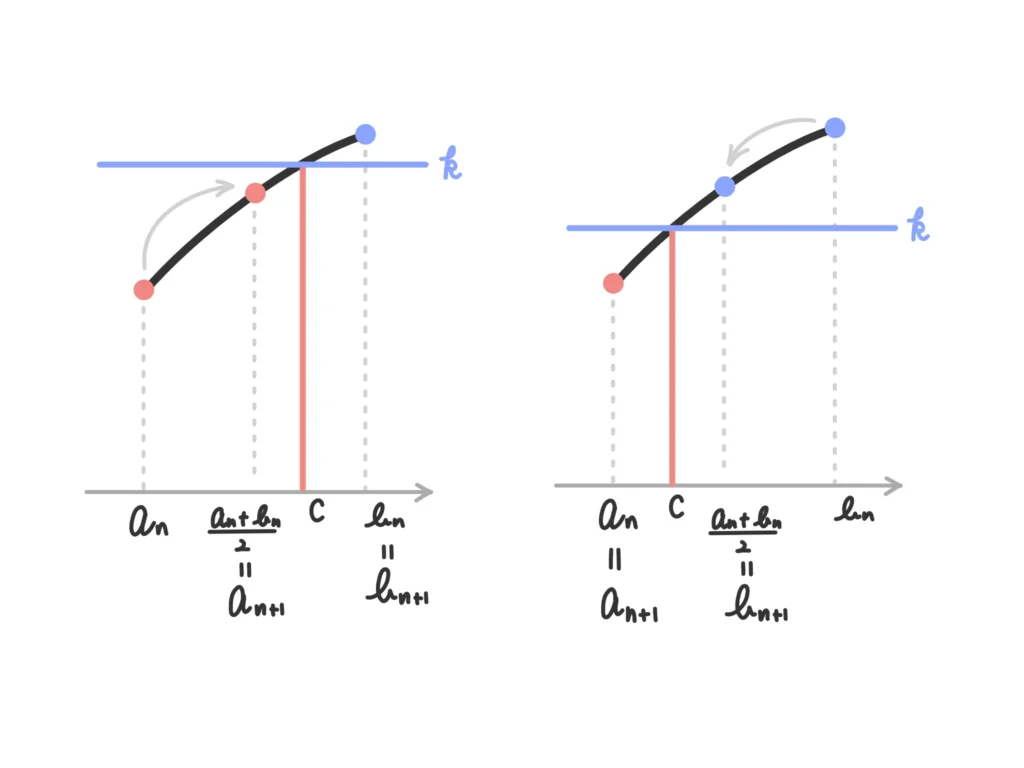

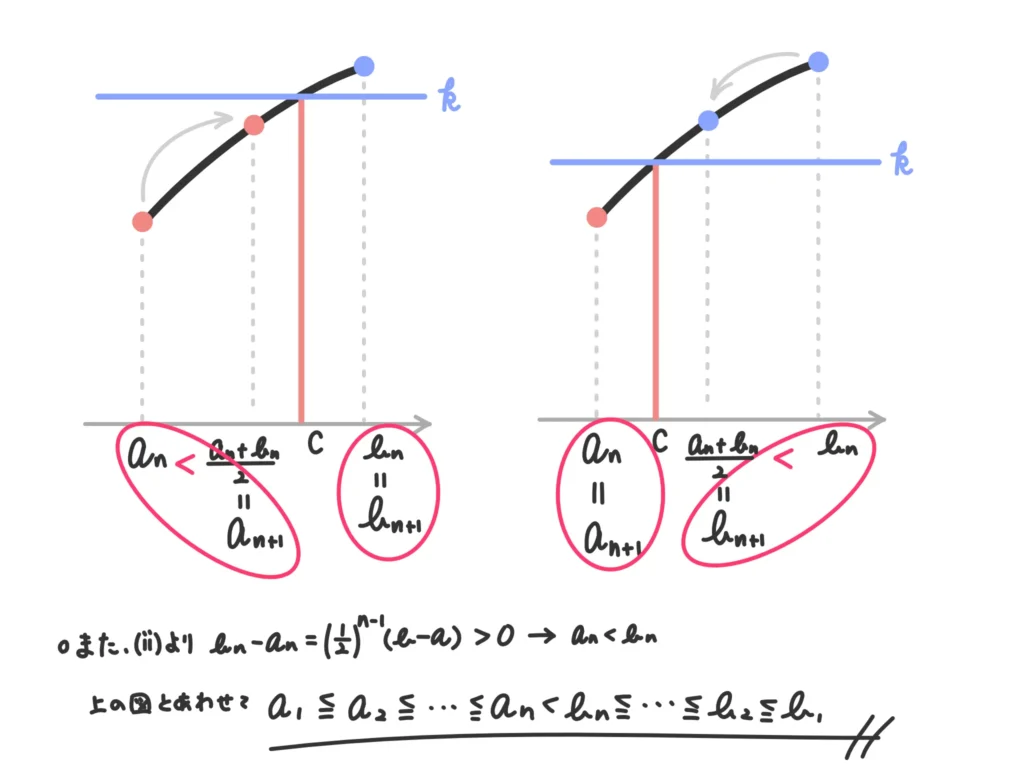
すると、数列\(\{a_n\}\)、\(\{b_n\}\)は次のような性質をもちます。証明はのちほど。
(ⅰ)\(a_1 \leq a_2 \leq \cdots \leq a_n < b_n \leq b_{n-1} \leq \cdots b_1 \)
(ⅱ)\(\displaystyle b_{n} – a_{n} = \left( \frac{1}{2} \right)^{n-1}(b-a)\)
(ⅲ)\( f(a_n) \leq k < f(b_n) \)
(ⅰ)より、有界な単調増加(減少)数列は収束する(この値を超えない、というラインがあって、増加し続ける数列は収束するという性質があります。単調減少も同じ。)
ので、数列\(\{a_n\}\)、\(\{b_n\}\)はそれぞれ収束します。
\(\displaystyle \lim_{n \to \infty}a_n = \alpha\)、\(\displaystyle \lim_{n \to \infty}b_n = \beta\)とおくと、
(ⅱ)より、\(\displaystyle \lim_{n \to \infty}(b_n -a_n) = 0\)なので、\(\displaystyle \lim_{n \to \infty}a_n = \displaystyle \lim_{n \to \infty}b_n\)。よって、\(\alpha = \beta\)。
\(\alpha = \beta = c\)とすると、
\(\displaystyle \lim_{n \to \infty}f(a_n) = f(\alpha) = f(c)\)、\(\displaystyle \lim_{n \to \infty}f(b_n) = f(\beta) = f(c)\)なので、(ⅲ)より、はさみうちの原理から、
\(\displaystyle \lim_{n \to \infty}k = f(c)\)。よって、\(k = f(c)\)。(終)
【(ⅰ)の証明】
下の図で証明したこと、としましょう。

【(ⅱ)の証明】
\(\displaystyle f \left( \frac{a_n + b_n}{2} \right) \leq k\)のときでも、\(\displaystyle f \left( \frac{a_n + b_n}{2} \right) > k\)のときでも、
\(\displaystyle b_{n+1} -a_{n+1} = \frac{1}{2}(b_n-a_n)\)となります。(実際に計算してみて下さい!)
数列\( \{ b_n-a_n \} \)は初項\(b_1 – a_1 = b-a\)、公比\(\displaystyle \frac{1}{2}\)の等比数列なので、
\(\displaystyle b_{n} – a_{n} = \left( \frac{1}{2} \right)^{n-1}(b-a)\)(終)
【(ⅲ)の証明】
\( f(a_n) \leq k < f(b_n) \)を示す。
数学的帰納法より、
\(n=1\)のとき\( f(a_1) \leq k < f(b_1) \)を示さなくてはならないが、最初に\(f(a) < k < f(b)\)と条件をつけたので成立。
\(n = l\)のときに\( f(a_l) \leq k < f(b_l) \)が成り立つと仮定する。
\(n = l+1\)について、
\(\displaystyle f \left( \frac{a_l + b_l}{2} \right) \leq k\)のとき、\(\begin{cases} \displaystyle a_{l+1} = \frac{a_l + b_l}{2} \\ b_{l+1} = b_l \end{cases}\)なので、
\(\displaystyle f(a_{l+1}) = f \left( \frac{a_l + b_l}{2} \right) \leq k\)が成り立ち、
仮定より\(k < f(b_l) = f(b_{l+1})\)なので、
\(f(a_{l+1}) \leq k < f(b_{l+1}) \)。
\(\displaystyle f \left( \frac{a_l + b_l}{2} \right) > k\)のとき、\(\begin{cases} a_{l+1} = a_l \\ \displaystyle b_{l+1} = \frac{a_l + b_l}{2} \\ \end{cases}\)なので、
仮定より\(f(a_{l+1}) = f(a_l) \leq k\)、
また、\(\displaystyle k < f \left( \frac{a_l + b_l}{2} \right) = f(b_{l+1})\)が成り立つので、
\(f(a_{l+1}) \leq k < f(b_{l+1}) \)。
以上から、\( f(a_n) \leq k < f(b_n) \)。(終)



\(\{a_n\}\)、\(\{b_n\}\)が\(c\)に寄っていく感じが面白いですよね。
中間値の定理の注意点
イメージ的には「当たり前じゃん…」と思う中間値の定理ですが、1点だけ注意してほしいポイントがあります。
それは、条件である「関数\(f(x)\)が閉区間\([a,b]\)で連続」というところです。



「連続じゃなかったら困る」という例を見てみましょう。
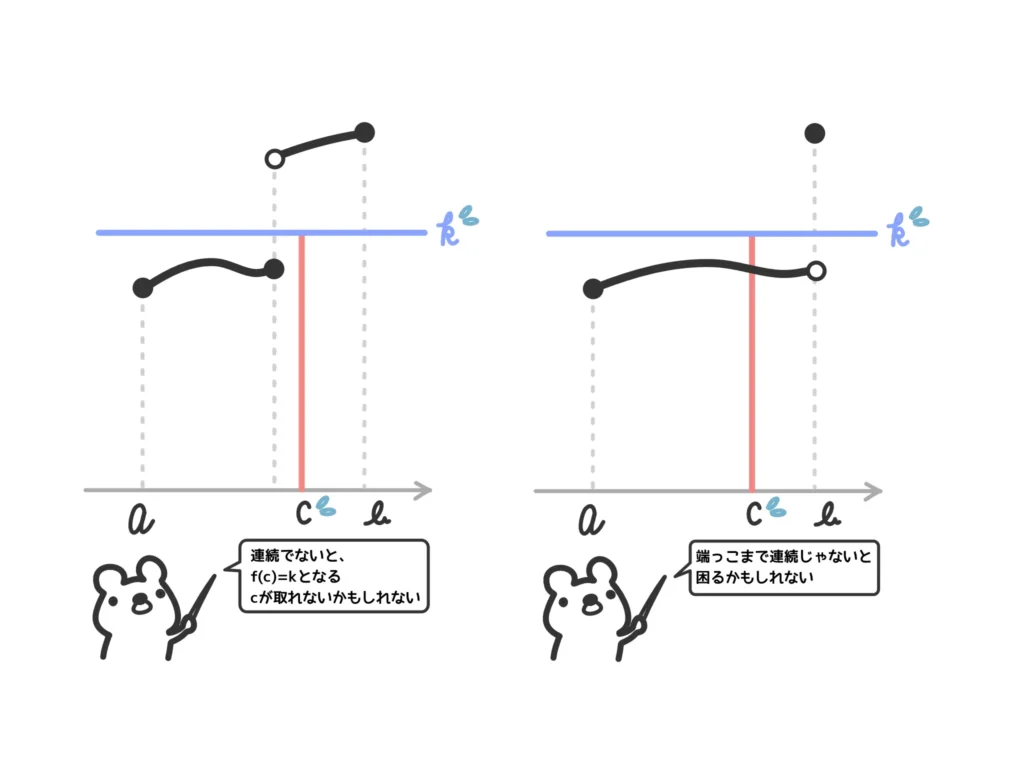

ということで、中間値の定理を使う際には「関数\(f(x)\)が閉区間\([a,b]\)で連続」と言いましょう!
中間値の定理を実際に使ってみよう!
方程式の解の存在の証明などで、中間値の定理をよく使います。
中間値の定理から言えること
関数\(f(x)\)が閉区間\([a,b]\)で連続で、\( f(a)\)と\(f(b)\)が異符号ならば、
方程式\(f(x) = 0\)の実数解が\(a\)と\(b\)の間に少なくとも1つ存在する。

例.方程式\(x – \cos{x} = 0\)は\(0 < x < \pi\)の範囲に少なくとも1つ実数解を持つことを示せ。
要は「連続だし、端っこの値が+(プラス)とー(マイナス)だから、+とーをまたぐときに\(f(x)=0\)となるところがあるよね」と言えばOKです。
(解答)
\(f(x) = x – \cos{x}\)とおくと、\(f(x)\)は区間\([0,\pi]\)で連続である。(←証明したいのは「\(0 < x < \pi\)の範囲」だが、「連続」というときの区間は端っこも含める。)
\(f(0) = -1 < 0\)、\(f(\pi) = \pi + 1 > 0\)なので、
方程式\(f(x) = 0\)、つまり\(x – \cos{x} = 0\)は\(0 < x < \pi\)の範囲に少なくとも1つ実数解を持つ(終)
中間値の定理の練習問題
問.\(x\)の方程式\(3x \log{x} + 1 = 0\)が\(\displaystyle \frac{1}{2} < x < 1\)に少なくとも1つ実数解をもつことを示せ。
答え
省略
中間値の定理まとめ
中間値の定理についてでした。
高校範囲では実数解の存在証明、くらいでしか使いませんが、平均値の定理の証明に使ったりもするので、ポイントは掴んでおきましょう。