PR
平均値の定理とは?様々な「平均値の定理」完全版!【証明から例題まで】
平均値の定理は数学Ⅲで習う定理です。
正直、最初は「なんでこんなもの習うんだろう…」と思うような定理です。いや…ハッキリ言って最後まで「あの、平均値の定理ってのはなんだったんだろ…」と思うような定理です。
高校(大学入試)での学習内容では、とってつけたような問題しかありませんが、実は、微積分の根幹の話をするときにはかなり重要な役割があります。
 せんせ
せんせ高校では微積分の根幹の部分をそこまで詳しく学習しませんからね。「連続」とか「微分可能」とかもそうですが、微積分をやるなら一応知っておくべき基礎、みたいなもんですね。
この記事では平均値の定理の証明とどのようなときに使うのか、それと様々なタイプの平均値の定理について説明します。
平均値の定理とは?
(遠足で山に登ってるみたいですよ)



やばい…この坂きつい…。なんでこんな修行みたいな山登りしないといけないんだ…。さっきから全く平坦な道が無いぞ…。山登りって言ってもちょっとくらい、こう、ハイキング的な要素あるだろ…。



(キツいと言いながら、セリフ長い。うるさい。)



もう少しでてっぺんですから。そこについたらお昼ご飯ですよ。



この調子だと大丈夫かな…。



ん?何がですか?体調悪いんですか?



いや、お昼、カップラーメンとコンロを持ってきたからお湯沸かして食べようと思ってるんですけど、こんなに坂道ばっかりだと、お湯沸かせるくらい平坦なところがあるかな、って心配です。



…先生は遠足のお昼ご飯にカップラーメンを食べようとしているあなたが心配です。


ということで、平均値の定理です。
平均値の定理の証明をする際に重要な、「ロルの定理」という定理があります。(というか、平均値の定理はほぼロルの定理の変形です。)
このあと説明しますが、ロルの定理は「\(a \leq x \leq b\)で、関数が\(f(a) = f(b)\)となるなら、\(a\)から\(b\)の間に\(f'(c) = 0\)となる\(c\)がどこかに1ヶ所以上ある」という定理です。
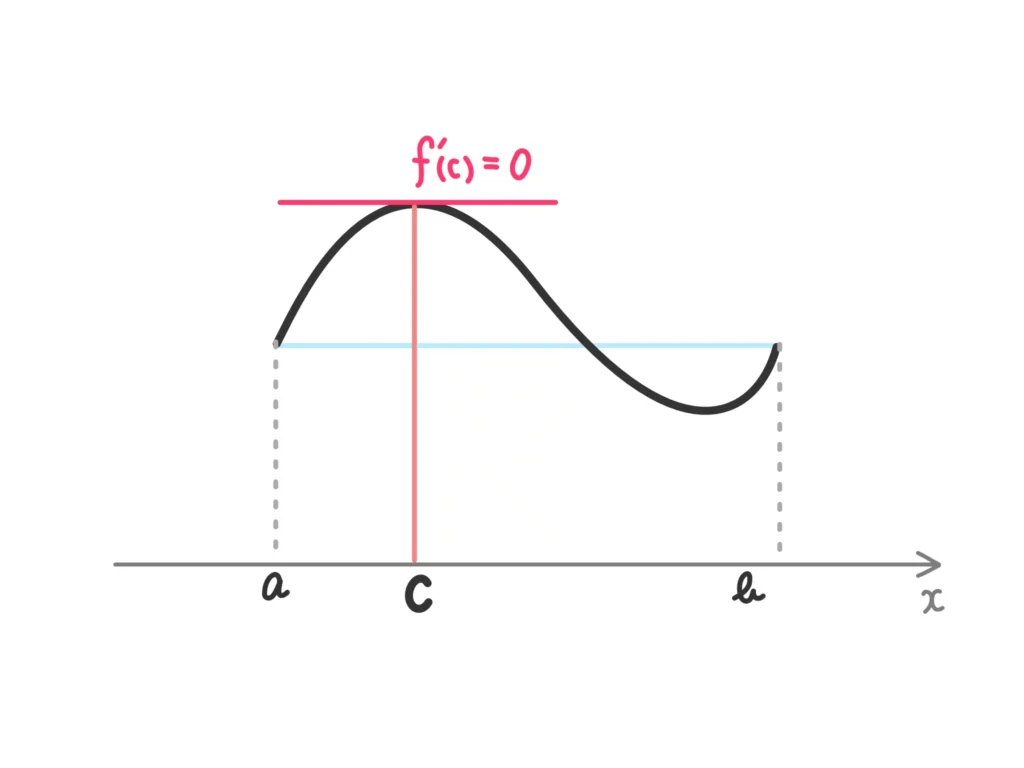

簡単に言うと「\(a\)から\(b\)の間のどこかに平坦になる(=接線の傾きが0になる)ところがある」ということですね。



よかった…お湯を沸かせる場所が保証されたぞ。(←実際のロルの定理は条件を押さえるのが重要です)
平均値の定理の証明
それでは平均値の定理の確認と証明をしていきましょう。
平均値の定理(ラグランジュの平均値の定理)
関数\(f(x)\)が区間\( [a , b]\)で連続で、区間\( (a, b) \)で微分可能ならば、
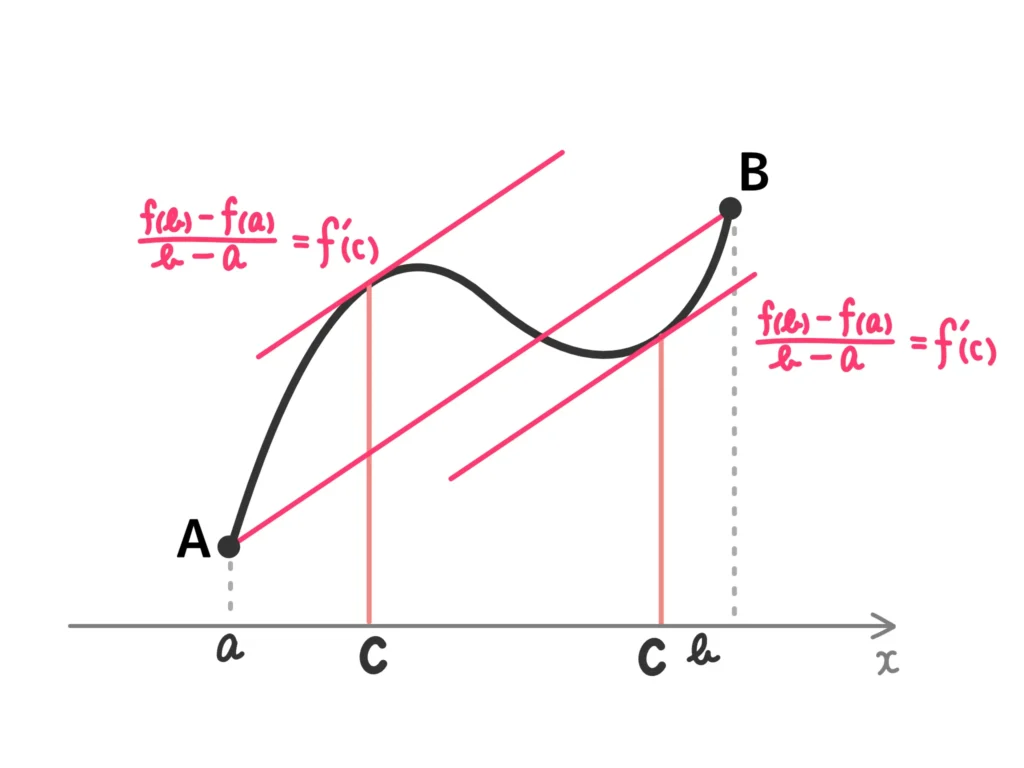
\(\displaystyle \frac{f(b) – f(a)}{b-a} = f'(c)\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。


平均値の定理の意味は、関数\(f(x)\)上に点\(A(a, f(a))\)、\(B(b, f(b))\)をとって、直線ABの傾きを考えたとき、その傾きと同じ傾きを持つ接線がある、ということです。
ちなみに、その接線は1本とは限りません。




それでは、平均値の定理を証明していきましょう。
ロルの定理の証明
先ほども説明しましたが、平均値の定理の核となるロルの定理というものがあります。
ロルの定理
関数\(f(x)\)が区間\( [a , b]\)で連続で、区間\( (a, b) \)で微分可能のとき、
\(f(a) = f(b)\)となるならば、
\(f'(c) = 0\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。


(証明)
(ⅰ) 区間内で\(f(x) = c\)(定数関数)のとき
\(f(a) = f(b)\)は満たすし、定数関数なので\(f'(x) = 0\)
つまり、\(a < c < b\)のどの\(c\)でも\(f'(c) =0\)となります。



ここからは、ちょっとでも\(f(a)\)(\( = f(b)\))より大きい部分があるとき、小さい部分があるとき、に分けて証明していきます。
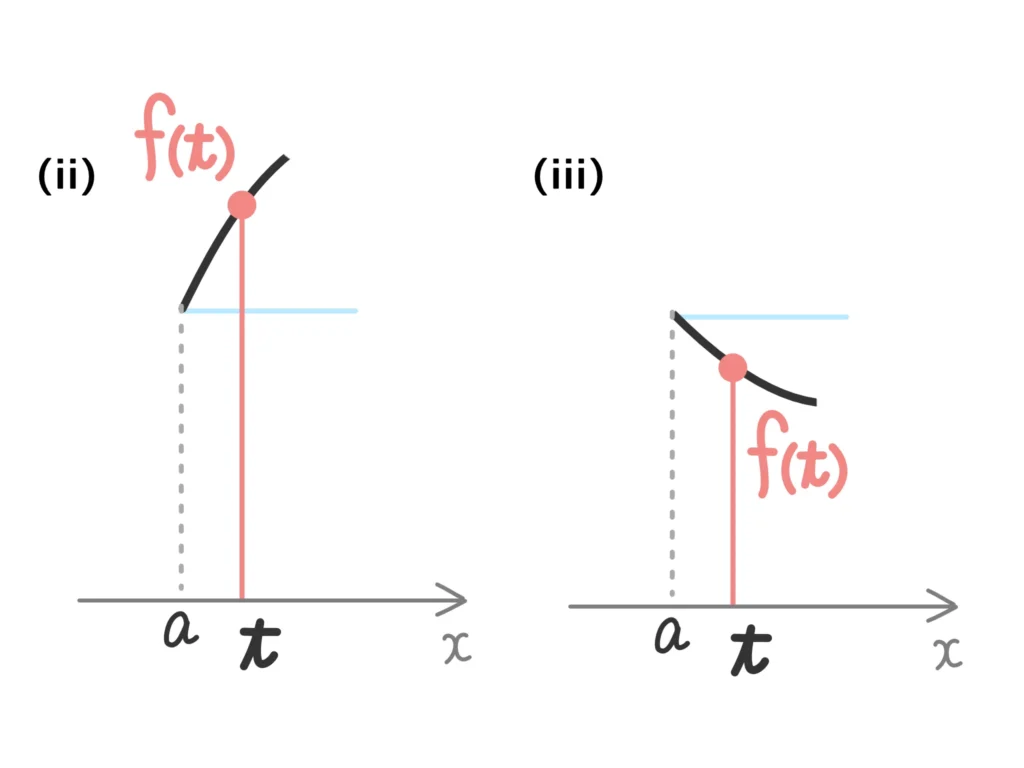

(ⅱ) \(f(a) < f(t)\)となる\(t\)があるとき(\(f(a)\)よりも大きい部分があるとき)
最大値の定理(有界閉区間上の連続関数は最大値を持つ)より、
\(a < c < b\)で\(f(c)\)が最大となるような\(c\)が存在します。
この最大となる\(c\)で\(f'(c) = 0\)となることを示します。
\(f(c)\)は最大値なので、ちょっとでもずれた\(x = c+h\)について、\(f(c) \geq f(c+h)\)が成り立ちます。
また、\(x = c\)で微分可能なので、次の2つの極限値は存在します。
が、\(f(c) \geq f(c+h)\)より、同時に符号もわかります。
\(\displaystyle f'(c) = \lim_{h \to +0} \frac{f(c+h) – f(c)}{h} \leq 0\)
\(\displaystyle f'(c) = \lim_{h \to -0} \frac{f(c+h) – f(c)}{h} \geq 0\)
よって、この2つの式を同時に満たす\(f'(c)\)は\(f'(c)=0\)しかありません。
(ⅲ) \(f(a) > f(t)\)となる\(t\)があるとき(\(f(a)\)よりも小さい部分があるとき)
(ⅱ)と同様に、\(a < c < b\)で\(f(c)\)が最小となるような\(c\)が存在します。
あとの証明方法は(ⅱ)の最大値を「最小値」と読み替えれば同じなので割愛します。
(終)
平均値の定理の証明
ロルの定理を使えば一発です!



\(f(a) = f(b)\)とならない一般的な関数をズルっとずらすことで、\(f(a) = f(b)\)となる状況を作ります。
(証明)
いきなりですが、
\(\displaystyle g(x) = f(x) – \left\{ \frac{f(b)-f(a)}{b-a}(x-a) + f(a) \right\} \)
という関数(差関数、という)を考えます。



ちなみに、\(f(x)\)から引いている部分、\(\displaystyle y=\frac{f(b)-f(a)}{b-a}(x-a) + f(a)\)は直線ABのことですね。
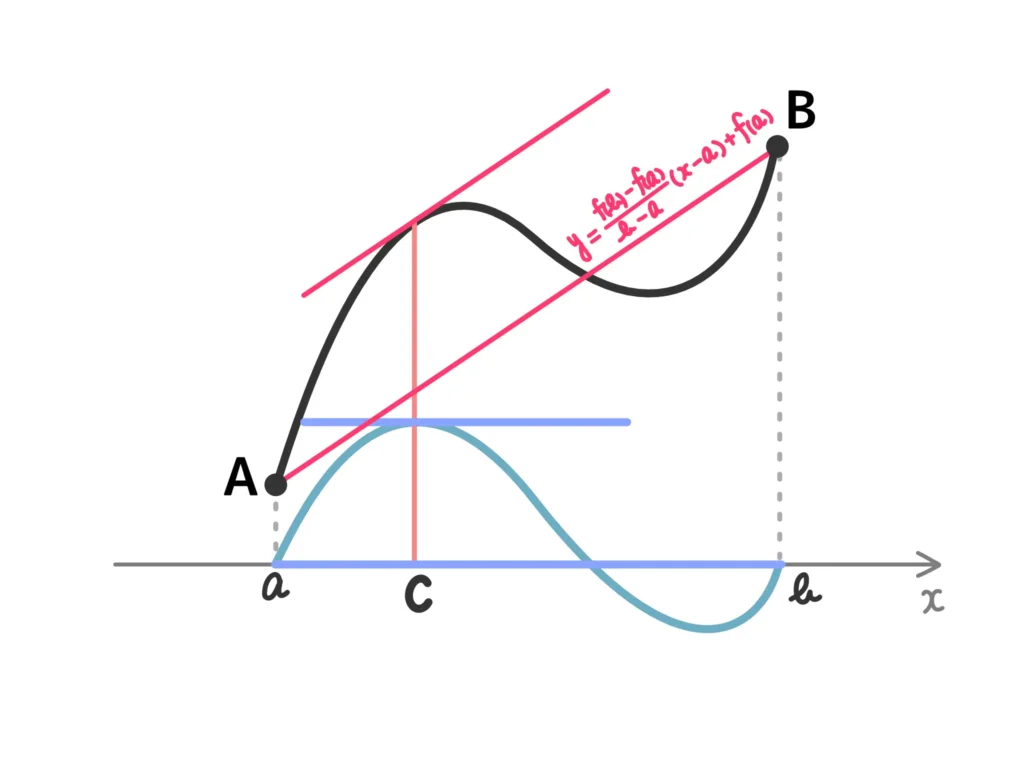

この関数は、
\(\displaystyle g(a) = f(a) – \left\{ \frac{f(b)-f(a)}{b-a}(a-a) + f(a) \right\} = f(a) -f(a)= 0 \)
\(\displaystyle g(b) = f(b) – \left\{ \frac{f(b)-f(a)}{b-a}(b-a) + f(a) \right\} =f(b)-(f(b)-f(a)+f(a)) = 0 \)
なので、\(g(x)\)は、区間\( [a , b]\)で連続で、区間\( (a, b) \)で微分可能の、\(g(a) = g(b)\)を満たす関数。
よって、ロルの定理が使えて\(g'(c) = 0\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。
ここで、\(\displaystyle g'(x) = f'(x) -\frac{f(b)-f(a)}{b-a}\)なので、\(\displaystyle g'(c) = f'(c) -\frac{f(b)-f(a)}{b-a} = 0\)。
したがって、
\(\displaystyle \frac{f(b) – f(a)}{b-a} = f'(c)\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。(終)
【補足】
もう少し簡単な関数、\(\displaystyle g(x) = f(x) -\frac{f(b)-f(a)}{b-a}x \)で示してもOKです。
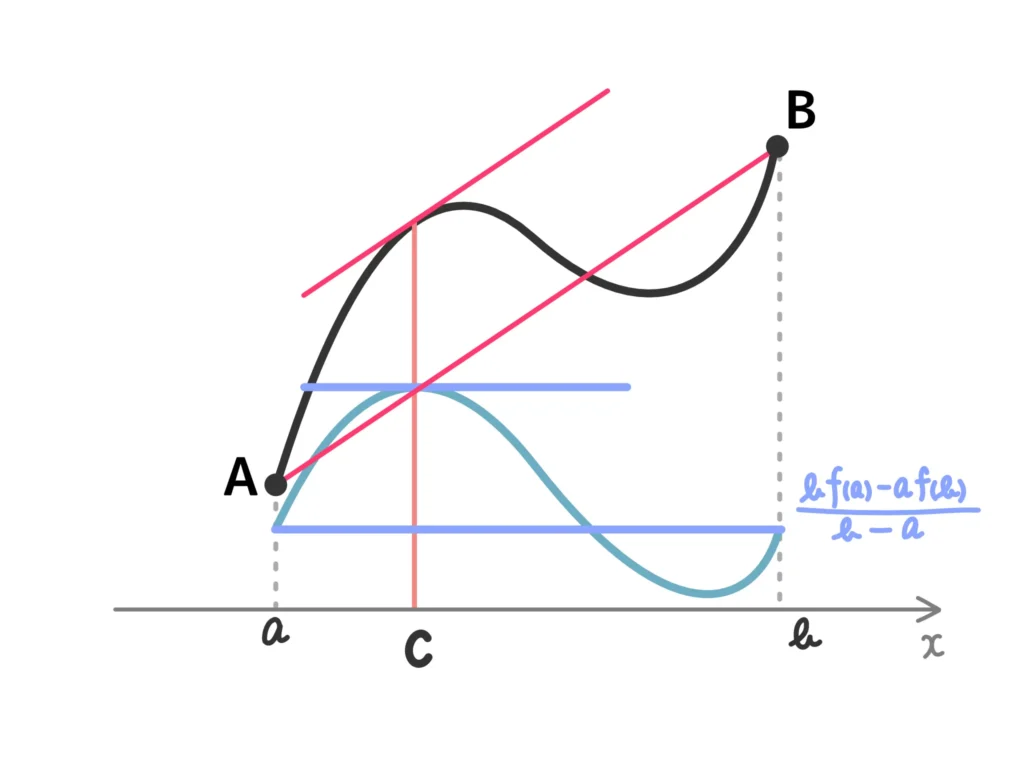

平均値の定理(コーシーの平均値の定理)
上で紹介した平均値の定理を少し発展させた「コーシーの平均値の定理」というのもあります。
平均値の定理(コーシーの平均値の定理)
関数\(f(x)\)、\(g(x)\)が区間\( [a , b]\)で連続で、区間\( (a, b) \)で微分可能(かつ、\(g(b)-g(a) \neq 0\))ならば、
\(\displaystyle \frac{f(b) – f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)}\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。(ただし、\(g'(c) \neq 0\))
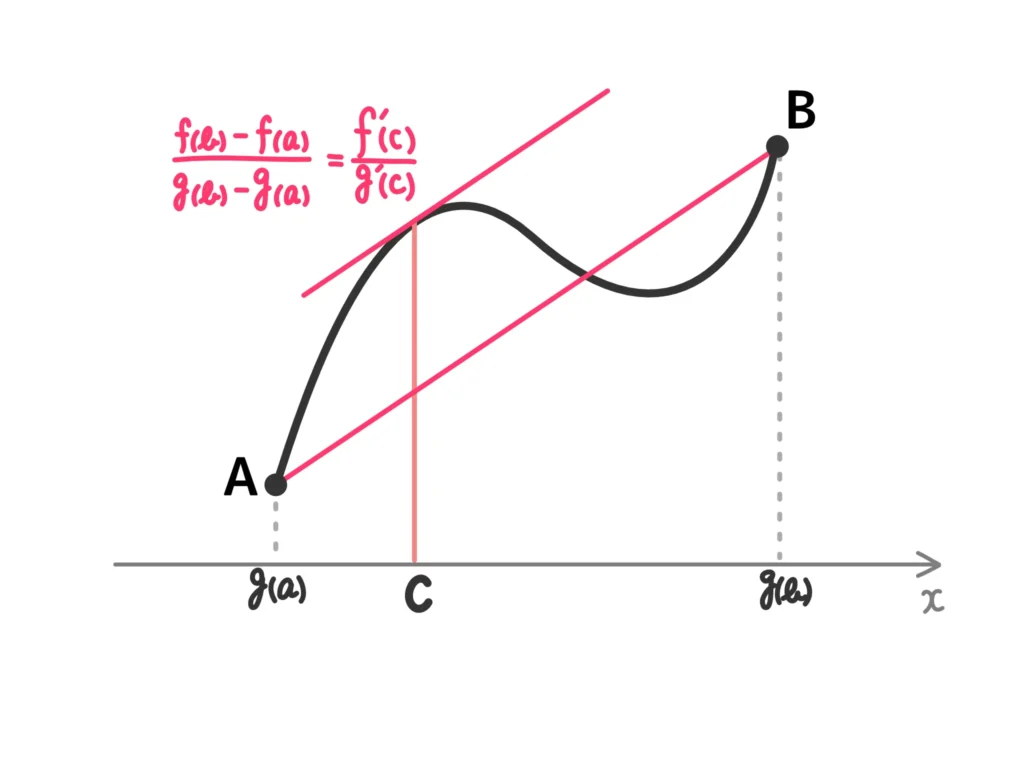

便宜上「関数\(f(x)\)、\(g(x)\)」と書いていますが、実際は\(y = f(t)\)、\(x = g(t)\)とした、平均値の定理の媒介変数バージョン、と捉えた方がいいです。
また、「大学入試で使ってはいけない」の代名詞、ロピタルの定理もこのコーシーの平均値の定理から証明できます。



ロピタルの定理は使用条件がかなり厳しいんですよね…。そもそも定理自体の証明が難しいですし。使ってはいけない…というよりも、正しく使うのが大変すぎるから、それなら普通に極限計算しなさい、という話です。
コーシーの平均値の定理の証明は、上の平均値の定理(ラグランジュの平均値の定理)の証明のように、上手くずらしてロルの定理を使う、という流れです。
コーシーの平均値の定理の証明
(証明)
こちらもいきなりですが、
関数\(\displaystyle h(x) = f(x) – \frac{f(b)-f(a)}{g(b)-g(a)}g(x)\)を考えます。
\(\displaystyle h(a) = f(a) – \frac{f(b)-f(a)}{g(b)-g(a)}g(a) = \frac{f(a)g(b)-f(b)g(a)}{g(b)-g(a)}\)
\(\displaystyle h(b) = f(b) – \frac{f(b)-f(a)}{g(b)-g(a)}g(b)=\frac{f(a)g(b)-f(b)g(a)}{g(b)-g(a)}\)
となるので、\(h(a) = h(b)\)。
よって、関数\(h(x)\)は区間\( [a , b]\)で連続で、区間\( (a, b) \)で微分可能、\(g(a) = g(b)\)となるので、ロルの定理より
\(h'(c) = 0\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在します。
ここで、\(\displaystyle h'(x) = f'(x) – \frac{f(b)-f(a)}{g(b)-g(a)}g'(x)\)なので、
\(\displaystyle h'(c) = f'(c) – \frac{f(b)-f(a)}{g(b)-g(a)}g'(c) = 0\)
したがって、
\(\displaystyle \frac{f(b) – f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)}\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在します。(ただし、\(g'(c) \neq 0\))(終)
積分型の平均値の定理
積分の形をした平均値の定理もあります!
積分型の平均値の定理
関数\(f(x)\)が区間\( [a , b]\)で連続ならば、
\(\displaystyle \frac{1}{b-a} \int_{a}^{b}f(x)dx = f(c)\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。
この式は\(\displaystyle \int_{a}^{b}f(x)dx = (b-a)f(c)\)とかくことも多い。
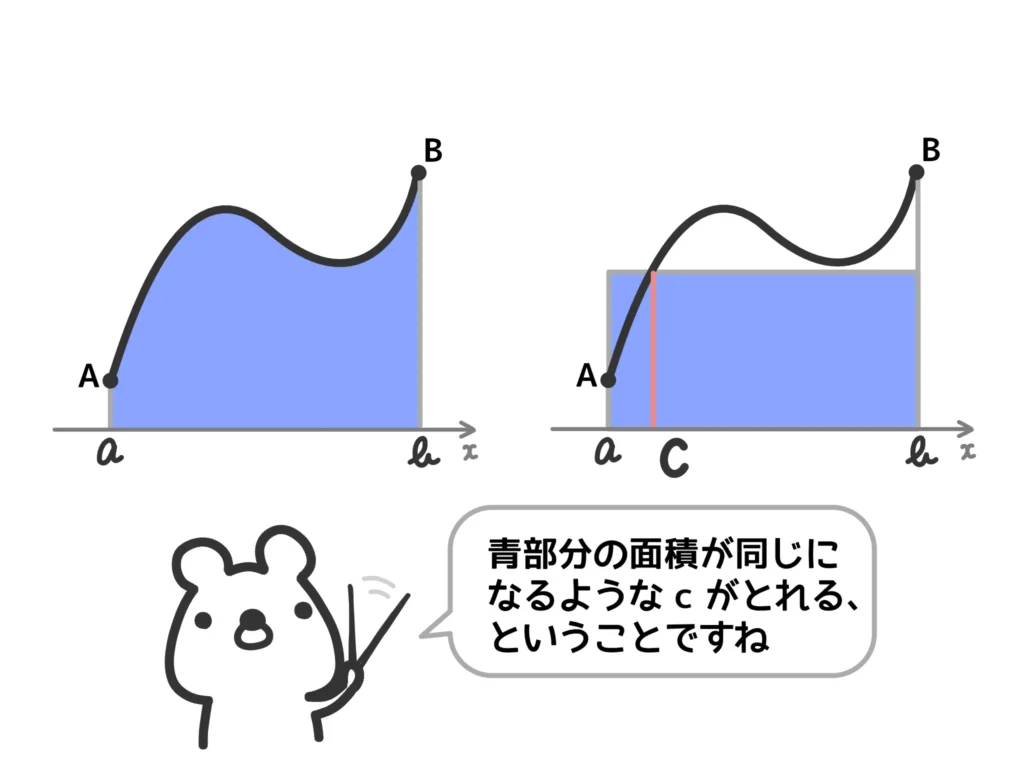

コチラの記事の「積分は微分の逆演算である」ことの証明に使っています。
積分型の平均値の定理の証明
(証明1)
区間\( [a , b]\)における\(f(x)\)の最大値を\(M\)、最小値を\(m\)とすると、
\( m \leq f(x) \leq M\)
\(\displaystyle \int_{a}^{b}mdx \leq \int_{a}^{b}f(x)dx \leq \int_{a}^{b}Mdx\)
\(\displaystyle (b-a)m \leq \int_{a}^{b}f(x)dx \leq (b-a)M \)
\(\displaystyle m \leq \frac{1}{b-a}\int_{a}^{b}f(x)dx \leq M \)…①
一方、\(f(x)\)は区間\( [a , b]\)で連続なので、中間値の定理より、
\(m \leq f(c) \leq M \)を満たす\(c\)が\(a < c < b\)に存在する。
この\(f(c)\)は\(m \leq f(c) \leq M \)を満たせばどのような値もとれるので、①より、
\(\displaystyle \frac{1}{b-a}\int_{a}^{b}f(x)dx = f(c) \)となる\(f(c)\)も存在する。(終)
(証明2)
\(\displaystyle F(x) = \int_{a}^{x}f(x)dx\)とおくと、\(F'(x) =f(x)\)。
\(F(x)\)は区間\( [a , b]\)で連続で、区間\( (a, b) \)で(当然)微分可能なので、平均値の定理より
\(\displaystyle \frac{F(b) – F(a)}{b-a} = F'(c)\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。
よって、\(\displaystyle \frac{1}{b-a} \int_{a}^{b}f(x)dx = f(c)\)となる\(c\)が\(a\)から\(b\)の間(\(a < c < b\))に存在する。(終)
平均値の定理はこんなときに使う
証明問題
例.\(a < b\)に対して、\(\displaystyle e^a < \frac{e^b-e^a}{b-a} < e^b\)を示せ。
ド定番ですね。
\(\displaystyle \frac{e^b-e^a}{b-a}\)みたいな感じで
「\(\displaystyle \frac{f(b)-f(a)}{b-a}\)の形(or変形した形)が見える不等式」+「その不等式に\(f(x)\)を微分した形が見える」
状況であれば、平均値の定理が使えます。
(証明)
\(f(x) = e^x\)とおくと、\(f(x)\)は区間\( [a , b]\)で連続で、区間\( (a, b) \)で微分可能なので、
\(\displaystyle \frac{f(b) – f(a)}{b-a} = \frac{e^b-e^a}{b-a} = f'(c)\)となる\(c\)が\(a < c < b\)に存在する。
一方、\(f'(x) = e^x\)は単調増加なので、
\(a < c < b\)より、\(f'(a) < f'(c) < f'(b)\)(←条件からこの不等式を作るのがポイント)
よって、\(\displaystyle e^a < \frac{e^b-e^a}{b-a} < e^b\)(終)
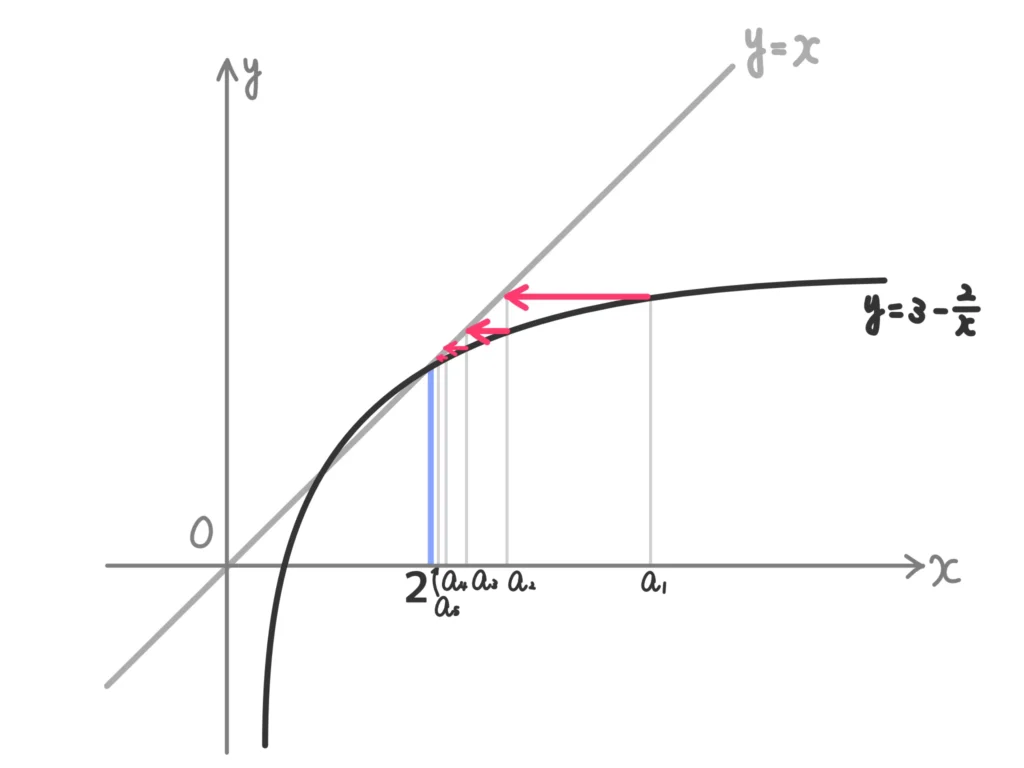
漸化式の極限
例.\(a_1 = 3\)、\(\displaystyle a_{n+1} = 3 – \frac{2}{a_n}\)のとき、次の各問いに答えよ。(\(n=1,2,3,\cdots\))
(1) \(a_n > 2\)を示せ。
(2) \(\displaystyle a_{n+1} -2 < \frac{1}{2}(a_n -2) \)を示して、\(\displaystyle \lim_{n \to \infty}a_n\)を求めよ。
これも定番ですが、平均値の定理を使う形が見えにくいので難易度は高めです。
ポイントは(2)の、一見漸化式の特性方程式を解いて変形したかのような形ですね。
もちろん、不等式ですし、そもそも与えられた漸化式が解けないので、この不等式の出どころは漸化式を変形したわけではありません。
ではどうするか…平均値の定理を使います!
(解答)
(1)は割愛。数学的帰納法を使えば証明できます。
(2)から解答していきます。
\(\displaystyle f(x) = 3-\frac{2}{x}\)とすると、\(f(x)\)は\( [2, a_n]\)で連続で、区間\( (2, a_n) \)で微分可能なので、
\(\displaystyle \frac{f(a_n) – f(2)}{a_n-2} = \frac{a_{n+1} -2}{a_n-2}= f'(c)\)となる\(c\)が\(2 < c < a_n\)に存在する。
(漸化式から\(\displaystyle f(a_n) = 3 – \frac{2}{a_n} = a_{n+1}\)、\(\displaystyle f(2) = 3 -\frac{2}{2} = 2\))
一方、\(\displaystyle f'(x) = \frac{2}{x^2}\)は\(2 < x < a_n\)において単調減少なので、
\( 2 < c (< a_n)\)から、\(f'(2) > f'(c)\)。
よって、\(\displaystyle \frac{1}{2} > \frac{a_{n+1} -2}{a_n-2}\)
\(a_n-2>0\)なので、\(\displaystyle a_{n+1} -2 < \frac{1}{2}(a_n -2) \)(終)
また、\(\displaystyle 0 < a_{n+1} -2 < \frac{1}{2}(a_n -2) \)となるので、
\(\displaystyle 0 < a_{n+1} -2 < \frac{1}{2}(a_n -2) < \left(\frac{1}{2}\right)^2(a_{n-1} -2) < \cdots <\left(\frac{1}{2}\right)^n(a_{1} -2) \)
\(a_1=3\)より、\(\displaystyle 0 < a_{n+1} -2 < \left(\frac{1}{2}\right)^n \)
\(\displaystyle \lim_{n \to \infty} \left(\frac{1}{2}\right)^n = 0 \)から、はさみうちの原理より
\(\displaystyle \lim_{n \to \infty} (a_{n+1} -2) = 0\)。つまり\(\displaystyle \lim_{n \to \infty} (a_{n} -2) = 0\)となるので、
\(\displaystyle \lim_{n \to \infty} a_{n} = 2\)…(答)
【補足】
正直、漸化式を使って変形した方が証明としてはラクです…。
(別解1)
(右辺)ー(左辺)\(\displaystyle = \frac{1}{2}(a_n -2) – (a_{n+1} -2)\)
\(\displaystyle \quad = \frac{1}{2}(a_n -2) – (3-\frac{2}{a_n} -2) = \frac{a_n^2 -4a_n + 4}{2a_n} = \frac{(a_n -2)^2}{2a_n} > 0\)
(別解2)
\(\displaystyle a_{n+1} = 3 – \frac{2}{a_n}\)より、
\(\displaystyle a_{n+1} -2 = 3 – \frac{2}{a_n} -2 \)
\(\displaystyle \quad = 1- \frac{2}{a_n} = \frac{1}{a_n}(a_n – 2) < \frac{1}{2}(a_n – 2)\)
(なぜならば、\(a_n > 2\)だから)
また、この極限のイメージは次のようになります。

平均値の定理の練習問題
問.関数\(f(x) = \log(x-1) + e\)(\(x>1\))について、次の各問いに答えよ。
(1) \(e+1 < x\)のとき、\(\displaystyle f'(x) < \frac{1}{e}\)を示せ。
(2) 数列\( \{ x_n\}\)を、\(x_1 = 4\)、\(x_{n+1} = f(x_n)\)で定めるとき、\(x_n > e+1\)を示せ。
(3) \(\displaystyle 0 < x_{n+1} – (e+1) < \frac{1}{e} \{ x_n-(e+1) \} \)を示し、\(\displaystyle \lim_{n \to \infty}x_n\)を求めよ。
答え
(1)省略
(2)省略
(3)省略、\(\displaystyle \lim_{n \to \infty}x_n = e+1\)
平均値の定理のまとめ
平均値の定理の総まとめでした。
数学Ⅲの教科書では「こういう定理があるよ」くらいにしか触れられませんが、一応高校生でも理解できるくらいの難易度で証明可能です。
「微積分の根幹を支える定理なんだ」くらいは知っておいてもいいかもしれません。