PR
組み合わせ(C)とは?【基本的な計算方法と順列(P)との違いを説明!】
順列(P)に続いて習う組み合わせ(C)。
「PとCはどう違うんだ?」とか「どういうときにPを使うのか、Cを使うのかわからん!」と疑問に感じる人も多いと思います。
この記事では組み合わせ(C)の基本的な計算方法から、Pとの違いまで解説していきます。
 デカ丸
デカ丸組み合わせは計算もちょっとコツがいります
組み合わせ(C)とは



だめだ…もう無理だ…



相変わらず何に悩んでるんだか…



父上にフィギュア片付けろって言われちゃったよ…。
「一つは展示室に、一つは書斎に、一つは自分の部屋に置いていいから」って…。



展示室…?展示室とは??



展示室が一番広いし空調設備も整ってるけど…。3つ選べても、どれを展示室に、書斎に、自分の部屋に置いていいか、決められないぜ!


ということで、組み合わせ(C)です。
組み合わせはその名の通り、たろうくんのように『順番をつけずに』とりあえず取ってくる組み合わせのパターンを計算する方法です。
まずはC(組み合わせ)の基本的な計算や性質を押さえていきます。
Cの計算方法
\( _{n}C_{r} = \frac{n \cdot (n-1) \cdots (n-r+1)}{r \cdot (r-1) \cdots 2 \cdot 1} \)



次のように覚えると計算しやすいです!
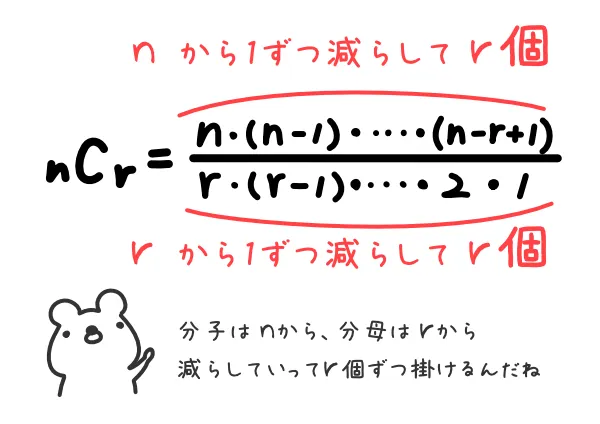

C(組み合わせ)がなぜこのような計算をするか、については次の記事に書いていますのであわせて御覧ください!


また、Cの次の性質と階乗を使った表現方法も押さえておいてください。
Cの性質・階乗を使った表現方法
・\( _{n}C_{r} = _{n}C_{n-r} \)
・\( _{n}C_{r} = \frac{n!}{r!(n-r)!} \)



特に\( _{n}C_{r} = _{n}C_{n-r} \)は計算上よく使います!
\( _{n}C_{r} = \frac{n!}{r!(n-r)!} \)は問題のレベルが上がると使うこともあります。こちらは「そういう表し方もあるんだぁ」くらいで。
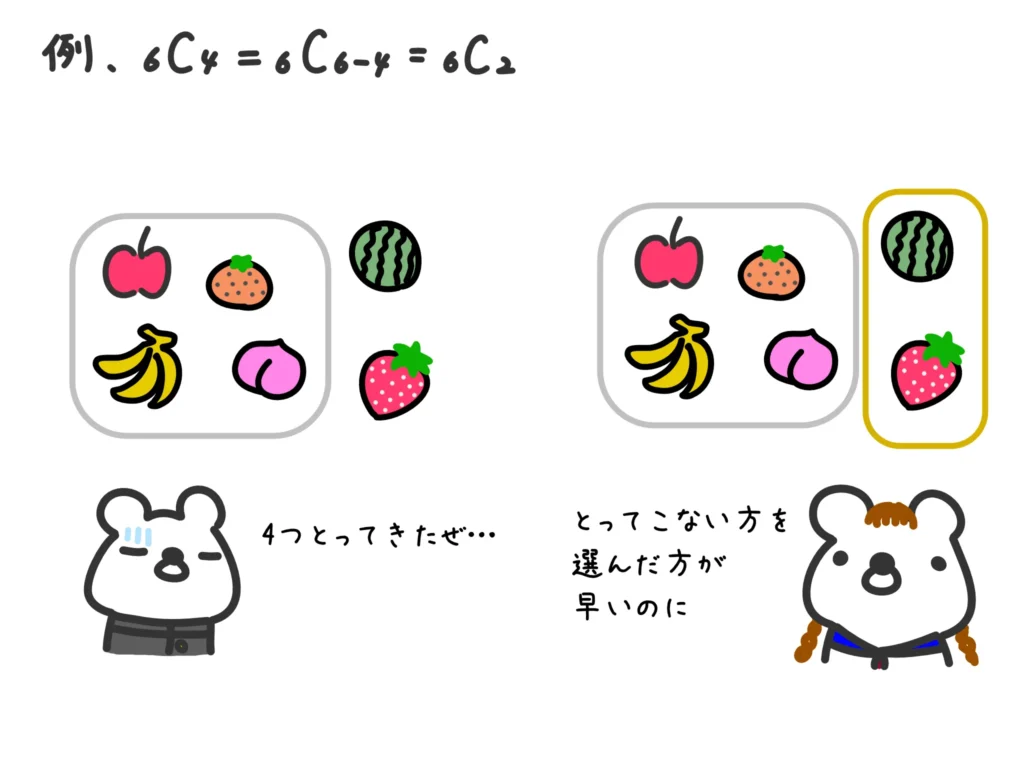
\(n\)個のものから\(r\)個とってくる組み合わせは、\(n\)個のものから、とってこない方の\((n-r)\)個を選ぶのと一緒、という意味です。
例.\(_{6}C_{4} = _{6}C_{6-4}= _{6}C_{2} \)

組み合わせ(C)と順列(P)の違い



んー…今度は\(C\)かぁ。この間習った\(P\)と書き方が似てるし…イマイチ区別がつかないなぁ。
よくあるのが「組み合わせ(\(C\))と順列(\(P\))の違いがわからない」という疑問です。
書き方も似ているので、どっちを使ったらいいか迷いますよね。


結論から言うと
「順番を考える必要がある」→順列 (\(P\))
「順番は考えていないor考える必要がない」→ 組み合わせ(\(C\))
という点に注意して使い分けましょう。



それでは、具体的に問題を考えながら\(P\)と\(C\)の違いを押さえていきましょう。
組み合わせ(C)と順列(P)の違いの簡単な例
例1.1、2、3、4、5の数字から2つをとってきて2桁の数を作る場合の数は?
これはPを使います。計算方法は、
\(_5P_2=5 \cdot 4 =20(通り)\)
です。例えば、1と2を使う2桁の数でも「1、2(つまり12)」と「2、1(つまり21)」では違う数になるからです。
順番を考える必要があるのでP(順列)を使います。
例2.1、2、3、4、5の数字から2つをとってくる組み合わせの数は?
これはC(組み合わせ)を使います。もう少し丁寧に説明すると「順番を考慮する必要がないから」ですね。計算は
\(_5C_2=\frac{5 \cdot 4}{2 \cdot 1} =10(通り)\)
となります。
先ほどと違って、1と2をとってくる組み合わせだけを考えるので「1、2」も「2、1」も組み合わせとしては同じものだと言えます。
順番を考える必要がないのでC(組み合わせ)を使います。
組み合わせ(C)と順列(P)の違いのもう少し詳しい具体例



よし、わかった!「順番を考える」→P(順列)を使う。「順番を考える必要がない」→C(組み合わせ)を使うんだな!



その通り!それでは、PとCの違いを考えながら、より実践的な例を見ていきましょう。
問.リンゴ、バナナ、みかん、ぶどう、なし、ももが1つずつ、合計6個ある。それを次のように分けるとき、それぞれの場合の数を求めよ。
(1) 6個から3個選んで、1人に配るとき。
(2) 6個から3個選んで、3人に1個ずつ配るとき。
(3) 6個から2個ずつ、3人に配るとき。



…いきなりよくわかんなくなったぞ。なんか似たような状況で、イマイチ区別がつかないんだけど。



似たような状況ですが、順番を考えるべきか?がポイントになります。(3)はCの応用ですね。
(1) これはCで計算します。3個の果物はとってくるだけで、その中で順番をつけているわけではないからです。
6個の中から3つ選ぶ組み合わせなので、
\(\displaystyle _6C_3=\frac{6 \times 5 \times 4}{3 \times 2\times 1}=20\)(通り)。
(2) これはPで計算します。
例えば同じ「リンゴ、バナナ、みかん」の組み合わせでも
「Aさん:リンゴ → Bさん:バナナ → Cさん:みかん」と配るのと、「Aさん:リンゴ → Bさん:みかん → Cさん:バナナ」と配るのは別物として考えないといけませんよね?
つまり、6個の果物のうち3個を、Aさん→Bさん→Cさんの順番に配っていることになります。
よって、\(_6P_3 = 6 \times 5 \times 4 = 120\)(通り)。
もしくは、単純に「Aさん:6通り → Bさん:5通り → Cさん:4通り」と考えてもいいです。無理にPを使う必要はありません。
(3) これはちょっと応用の考え方ですが、Cを使って計算します。



(2)と配る個数が変わっただけなのに、なんで(2)はPで、(3)はCなんじゃあ…
と思うかもしれません。



実際にCを使って解いてみましょう!
まずは、Aさんに2個配るための果物を選ばないといけません。この段階では選んだ2個の果物に順番をつける必要はないので、
\(_6C_2\)(通り)
となります。
次に、Bさんに2個配るための果物を選ばないといけません。これも同様に、\(_4C_2\)通り(←2個減ってるから、4個のうちから2個選ぶことになる)です。
最後に、Cさんに2個配るための果物を選ばないといけません。\(_2C_2\)通りです。(実際は残った2個を問答無用にCさんに配るので、1通りです。)
よって、\(\displaystyle _6C_2 \times _4C_2 \times _2C_2 = \frac{6 \times 5}{2 \times 1} \times \frac{4 \times 3}{2 \times 1}\frac{2 \times 1}{2 \times 1} = 15 \times 6 \times 1 = 90\)(通り)。
【補足】
(2)では、「Aさん:6通り → Bさん:5通り → Cさん:4通り」だから「\( 6 \times 5 \times 4\)」と計算しました。
これは、単純に1個選べばいいので、6通り→5通り→4通り、とすぐにわかったんですね。
(3)は、この「6通り→5通り→4通り」がすぐにわからないので、それぞれ\(C\)を使って計算したんだ、と思ってください。



なので、実は組み合わせと順列の考え方を両方使っています。
コチラの記事でも説明しましたが、「順列=Pで計算」と考えているとこういうときにわかりにくくなります。
あくまでPは表現方法です!実際は「順番に何通りずつあるか?」を掛ける、という考え方の方を押さえておいてください。
番外編.組み合わせ(C)の面白い性質
Cには次の様な性質もあります。
$$ _{n}C_{r} = _{n-1}C_{r-1}+_{n-1}C_{r} $$
これについては「特定の1つに注目して、それを含む組み合わせとそれを含まない組み合わせに分類して場合の数を求める」と説明されていることが多いです。



日本語シャベッテクダサイ…
ということで、こちらは次の図を見てください。
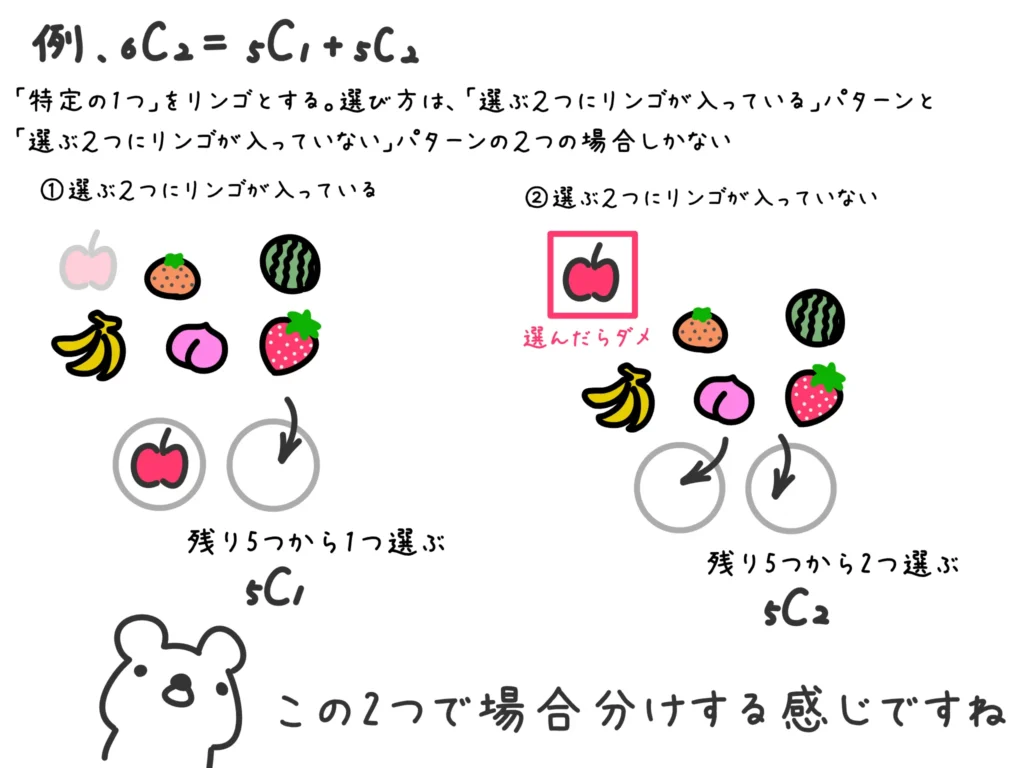




要は「場合分け」の考え方ですね
組み合わせの基本とその性質のまとめ
組み合わせの基本とその性質、順列(P)との違いについてでした。
順列(P)は「こういう表記方法があるんだ」程度でも実際に問題を解くのに困ることはありませんが、組み合わせ(C)はこの方法でしか計算できません。
ですので、計算方法と性質はしっかり押さえておきましょう。





