PR
指数関数のグラフで押さえておくべき重要な特徴3選
指数関数のグラフは単純な形をしていますが、実は重要な性質が隠れています。
この記事では、対数関数のグラフの重要な特徴について説明していきます。
指数関数のグラフ
 たろぅ
たろぅふっ…今日の「指数関数のグラフ」の授業は簡単だったな。いや、もうこの天才にあの程度の単純なグラフのことなんざ、一瞬で理解可能だね。



お、なんか今日はイキイキしてますね。



ふっ…せんせい…あんな単純な曲線、この僕にとっては朝飯前ですよ。なんてったって右上がりか右下がりかしかないんでしょ?二次関数や三角関数に比べたら楽勝ですよ。



右上がりになるときと右下がりになるときって何が違うの?



ん…?あれ?…えーっと…。なんかこう…気分?ハイな気分だったら右上がりで、落ち込んでたら右下がり、みたいな?



…。
ということで指数関数のグラフです。
たろうくんが言うように指数関数のグラフは単純な形をしていますが、実はいくつか重要な特徴があります。
指数関数のグラフ
指数関数\(y = a^x\)が表すグラフは次のようになる。ただし、底\(a\)は\(0 < a < 1\)または\(1 < a\)とする。(底\(a < 0\)のときはすべての実数\(x\)で\(a^x\)値が定義できないし、底\(a = 0,1\)のときは\(0^x=0\)、\(1^x = 1\)となるから)
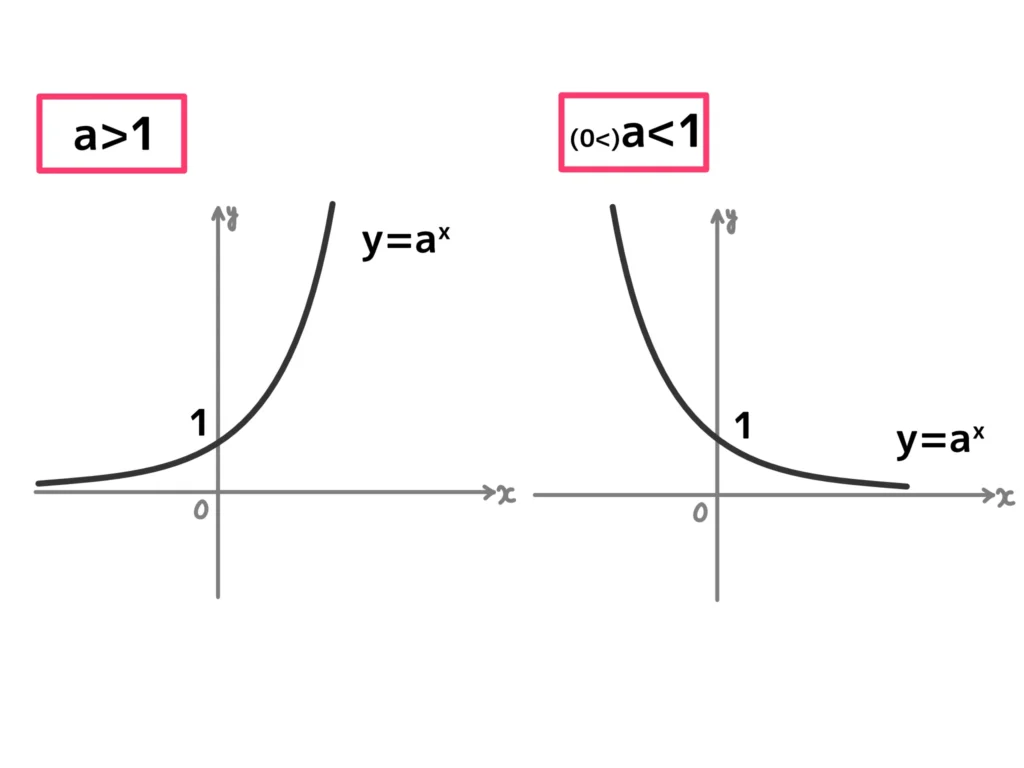

指数関数のグラフの特徴
指数関数のグラフにはいくつか押さえておくべき特徴があります。
これは、グラフというよりも、このあとの指数方程式・不等式などの問題を解く際によく使う性質になります。



グラフの形をアタマに入れておきながら、方程式や不等式を解く際にサッと指数関数の性質が出せるようにしておきましょう。
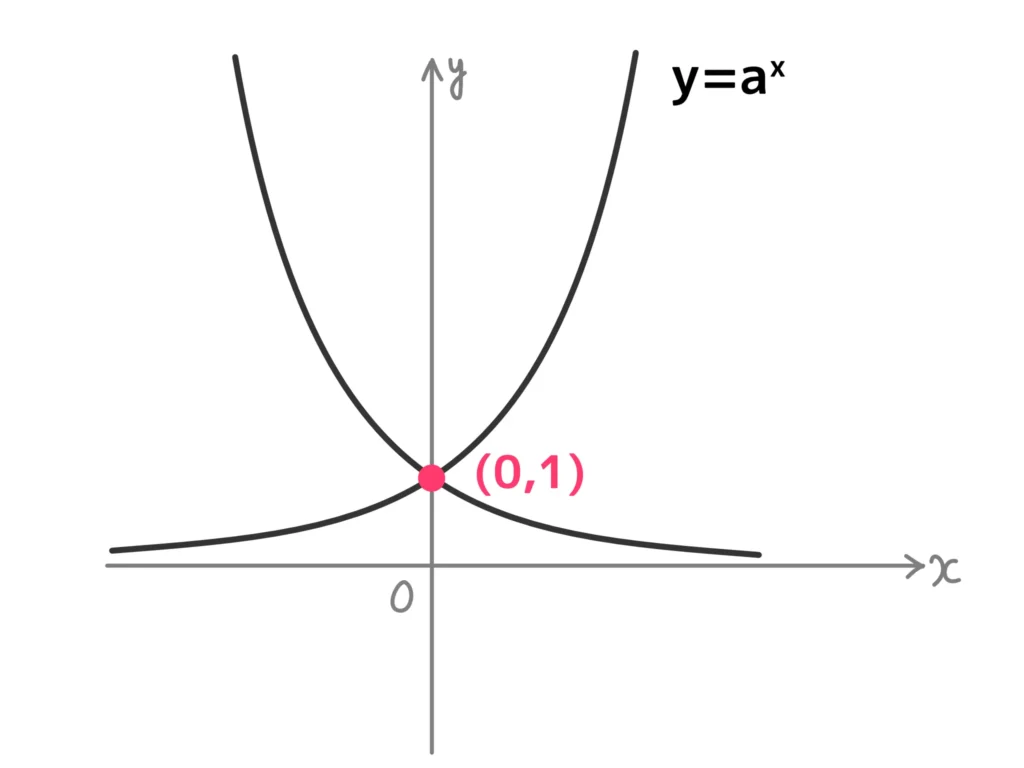
1.必ず点(0,1)を通る
これはわかりやすいです。どんな指数関数\(y = a^x\)でも、\(a^0=1\)となるので、必ず点\( (0,1) \)を通ります。

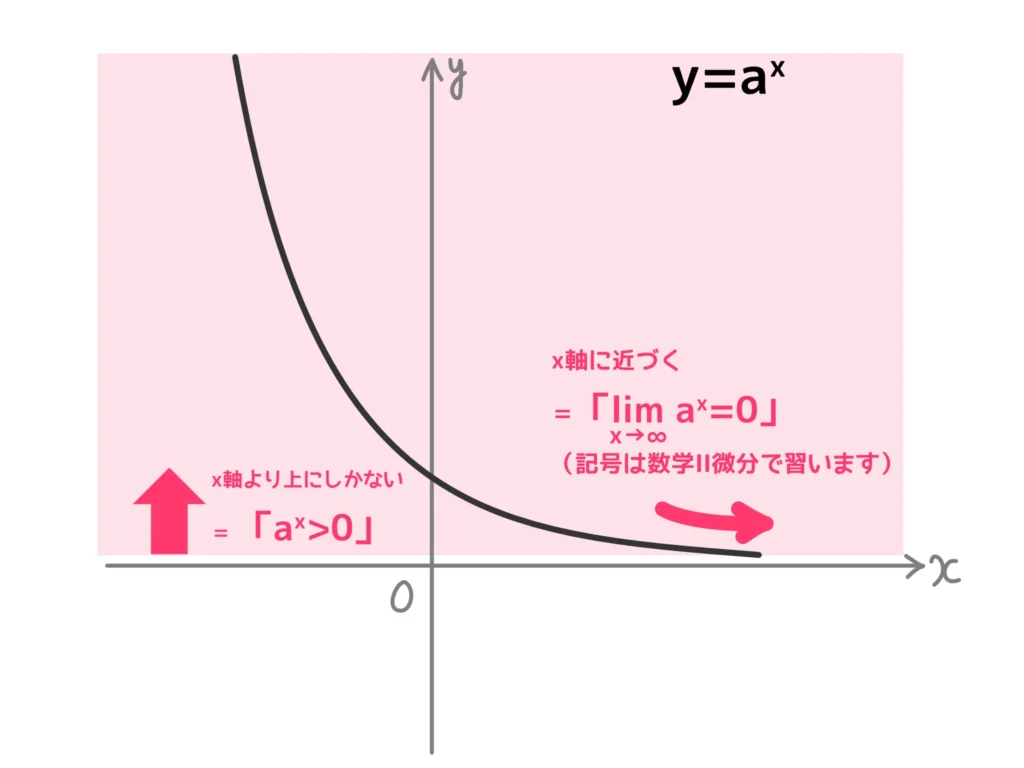
2.y>0、x軸が漸近線
これは結構重要です。
グラフとしては単純に「\(x\)軸より上の部分(\(y>0\))にグラフがある」ということと「\(x\)軸に近づく」という話になりますが、
このあとの指数方程式で置き換えが必要になったときや、数学Ⅲの極限で重要な性質になります。

例.方程式\(4^x-2^x+2 = 0\)を解け。
\(2^x = t\)と置かないといけませんが、そのとき\(2^x > 0\)なので\(t>0\)となることに注意しないといけません。



置き換えたら範囲に注意!です。
(解答)
\(4^x-2^x+2 = 0\)より
\((2^x)^2-2^x+2 = 0\)
\(2^x = t\)とおくと、\(t>0\)であり、
\(t^2-t+2 = 0\)となる。
\( (t+1)(t-2)=0\)
\(t = -1, 2\)
\(t>0\)より\(t = 2\)。
\(2^x = 2\)なので、\(x = 1\)…(答)
3.底a>1で単調増加、0<a<1で単調減少
かなり重要です。
このあと指数不等式を解く際に、必ず押さえなければいけないポイントになってきます。
なぜなら\(a^p > a^q\)という不等式が与えられた場合、指数部分\(p\)、\(q\)の大小関係が
「そのまま\(p>q\)」となるか?「ひっくり返って\(p < q\)」となるか?は
底\(a\)が\(a>1\)なのか\(0 < a < 1\)なのかによるからです。
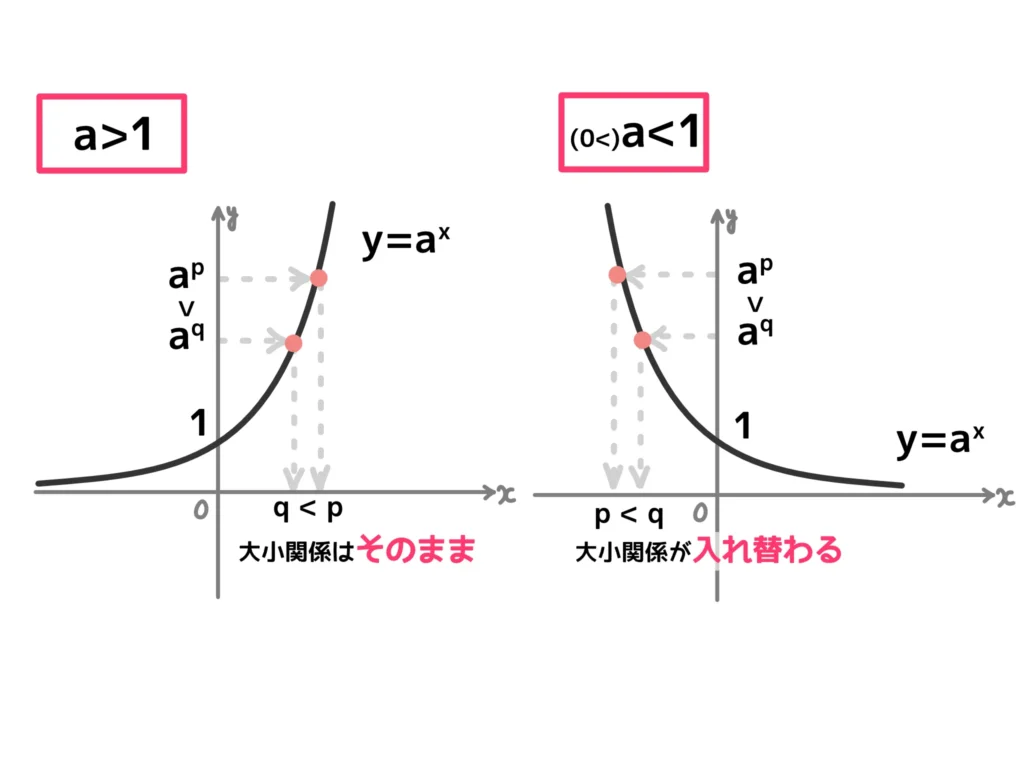




「指数関数の比較」↔「指数部分の比較」のタイミングで底\(a\)の値が1より大きいか?小さいか?を言いましょう。
おまけ1.底による対称性
これは「関数の性質」から言える指数関数の特徴です。
よくありますが、\(y = a^x\)と\(\displaystyle y = \left( \frac{1}{a} \right)^x\)は\(y\)軸対称です。
例.\(y = 2^x\)と\(\displaystyle y = \left( \frac{1}{2} \right)^x\)は\(y\)軸対称。
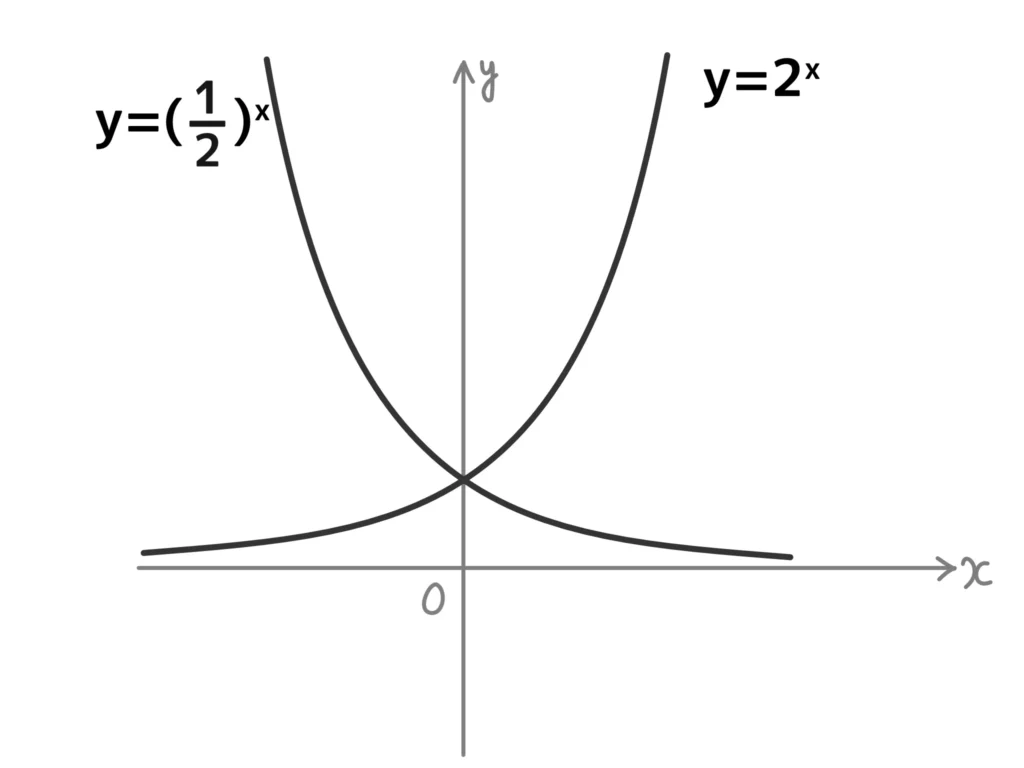

これは\(\displaystyle y = \left( \frac{1}{a} \right)^x = (a^{-1})^x = a^{-x}\)
となるからです。
コチラの記事で説明しましたが、関数\(f(x)\)の\(x\)を\(-x\)に置き換えたときに\(f(x) = f(-x)\)となれば\(y\)軸対称となります。(コチラは1つのグラフが\(y\)軸対称、という話なので、今回のように2つのグラフが\(y\)軸対称という話とはちょっと違いますが、考え方は同じです。)




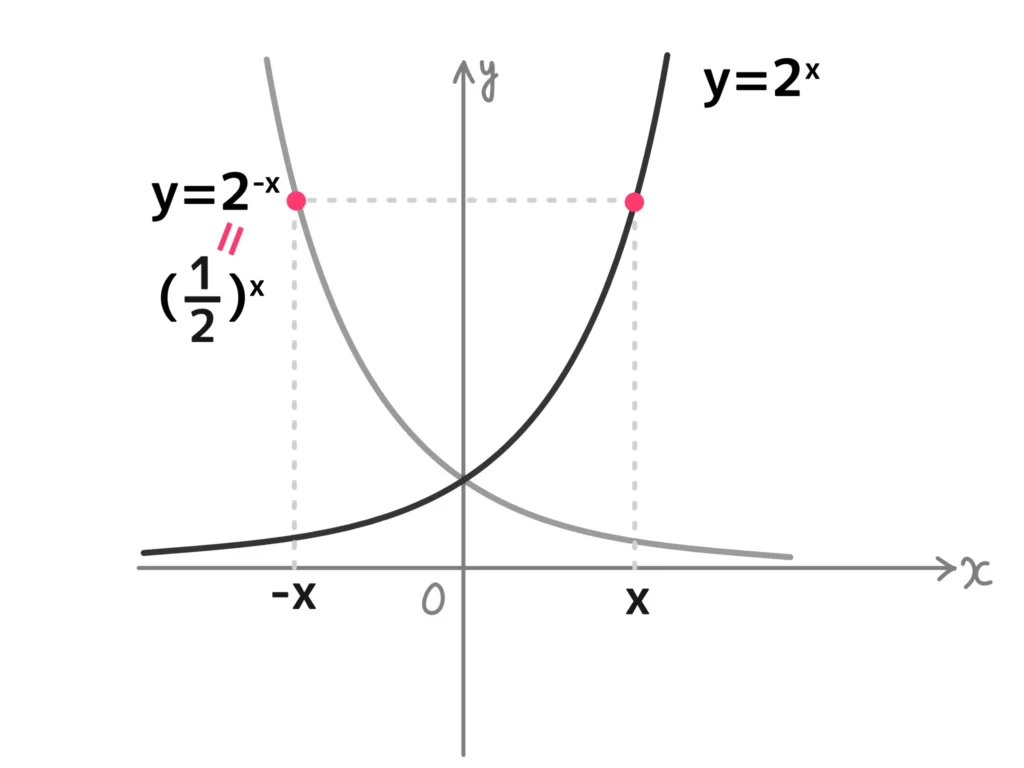
\(f(x) = a^x\)、\(\displaystyle g(x)= \left( \frac{1}{a} \right)^x = a^{-x}\)
とすると、\(f(-x) = a^{-x}\)となります。つまり、ある\(x\)に対して\(y\)軸と反対側の\(-x\)を考えるとそれが常に\(g(x)\)と同じになりますよね。

おまけ2.指数関数を「底のべき乗倍」したら平行移動!?
マニアックな感覚です。
タイトルがわかりにくいですが、つまり\(y = a^x\)に対して、
\( y = a^p \cdot a^x\)を考えよう、
ということです。
関数を実数倍しているので、グラフの感覚で言えば「\(y\)軸(縦)方向に伸ばすor縮める」という感じになります。
が、同時にこれが\(x\)軸方向の平行移動を表しています。
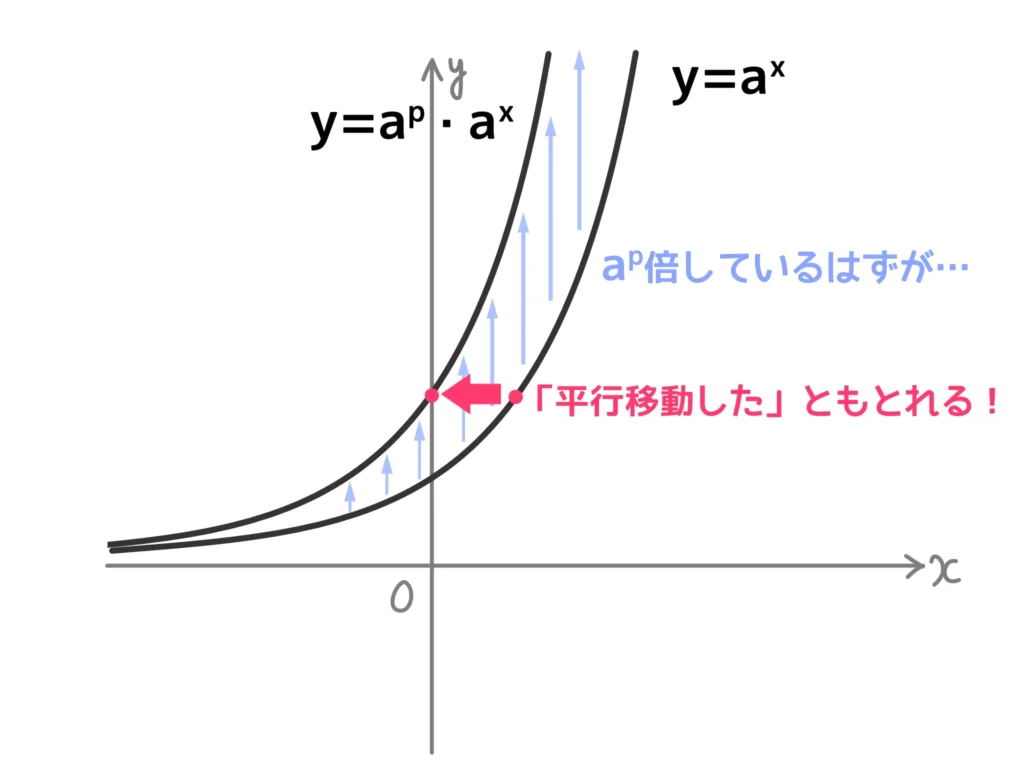

これは、\( y = a^p \cdot a^x= a^{x+p}\)となるからです。



縦に伸ばしたり縮めたりしているのに、横方向の平行移動、つまり全体としてみると形が変わっていない、というのは面白い感覚ですね。実際に使うか…と言えば、微妙ですが笑
ちなみに指数にも底の変換公式があるので、必ずしも「底の」べき乗倍である必要はありません。


何倍しようが、底の変換公式で底を揃えて(指数関数の次に勉強する「対数」の力を借りながら)平行移動の形にもっていくことができます。
例.\(y = 3 \cdot 2^x = 2^{\log_2 3} \cdot 2^{x} = 2^{x + \log_2 3}\)
指数関数のグラフまとめ
指数関数のグラフについてでした。
指数関数のグラフは単純な形ですが、指数方程式や不等式を解く際のポイントとなる特徴があるので、そこを押さえておくことは重要です。



グラフをかく、というよりも、このあとの方程式や不等式の話をするためにパッと指数の特徴が出てくるようにしておきましょう。





