PR
指数方程式・不等式の解き方のコツ【底の大きさに注意！？】
指数関数の方程式・不等式は記述上の注意点も多く、間違いやすい問題です。
この記事では、指数方程式・不等式を解く際の注意点やコツについて説明していきます。
目次
指数方程式・不等式とは？
たろぅアレ？どっちがどっちだろ…？
はなこん？どうしたの？
たろぅいや…アルバムの整理してたんだけど、写真が混じっちゃった…。同じ月に撮ったのはわかってるんだけど…どっちが新しくてどっちが古い写真だろ？
はなこあら、面倒なことしでかしたわね。ちょっと見せてよ。
たろぅ（言い方…）
たろぅあ！でもこの葉っぱの量が違う！これ見ればわかるんじゃない！？
はなこんー…。これ、何月に撮った写真なの？
たろぅん？何月？？何月に撮ったかな…？
でもそれ関係あるの？
ということで、指数方程式・不等式です。
冒頭…なぞなぞみたいな感じになってしまいましたが、皆さんはどっちが新しい写真でどっちが古い写真かわかりますか？
でもこれ、どっちが新しい写真か、わかんなくないですか？
たろぅいやいや、わかるでしょ！葉っぱの量が多い方が新しい写真でしょ！葉っぱ生えた後でしょ！
と思うかもしれませんが、例えばコレが「１１月に撮った写真」とわかったらどうでしょう？
たろぅう…。１１月…？１１月なら…葉っぱが散るだろうから、葉っぱが少ない方が新しい写真かも…。
と思いませんか？実は指数不等式を解く際にはこの考え方（？）が重要になってきます。
せんせま、ここの考え方は後ほど詳しく説明しましょう。まずは簡単な指数方程式・不等式を見てみましょう。
例えば次のような方程式・不等式を満たす\(x\)の値や範囲を求めるのが指数方程式・不等式を解く、という問題になります。
例１．\(2^x = 8\)
例２．\(2^x < 8\)
（解答）
例１．\(2^x = 8\)
\(2^x = 2^3\)
\(x=3\) …（答）
例２．\(2^x < 8\)
\(2^x < 2^3\)
底2は1よりも大きいので
\(x < 3\) …（答）
せんせ後ほど説明しますが「底を揃えて指数比較」が基本です。
ただ、例２の不等式の場合「底2は1よりも大きいので」という記述がポイントとなります。
指数方程式・不等式を解くコツ
最終的には
底を揃えて指数比較
をしていきます。
ただ、そこに至るまでに、上手く変形をしたり、置き換えて二次方程式・不等式を解かないといけなかったりします。
また、置き換えた場合は\(a^x > 0\)となることをアタマに入れておかないといけません。
せんせそれでは指数方程式、指数方程式それぞれでもっと具体的なコツを見ていきましょう。
指数方程式を解く
指数方程式は特に記述上問題になる部分はありません。
練習して、特に数字感覚を身につけていきましょう（後ほど説明します）。
簡単な指数方程式は「底を揃えて指数部分の比較」
簡単な指数方程式は底を揃えて指数比較、でいけます。
指数を揃えるために式変形をしないといけないので、そこだけちょっと練習する必要があります。
例３．\(2 \cdot 2^{x+3} = 32\)
最初の\(2\)は\(2^1\)とみなして指数法則を使うのがポイントです！
（解答）
\(2 \cdot 2^{x+3} = 32\)
\(2^{x+3+1}=2^5\)
\(2^{x+4}=2^5\)
よって\(x+4=5\)なので\(x=1\)…（答）
例４．\(27^x=729\)
数が大きくなるとわかりにくいですが、左辺も右辺も「\(3\)の△乗」の形に直すことができます。
（解答）
\(27^x=729\)
\((3^3)^x = 3^6\)
\(3^{3x}=3^6\)
よって、\(3x = 6\)なので\(x=2\)…（答）
せんせコツは、例えば\(64=2^6\)とか\(243=3^5\)とか…「この数字は◯の△乗」という数字感覚を、常に意識して身につけることですね。
複雑な指数方程式は置き換えがほとんど
複雑な形の指数方程式は置き換えることがほとんどですが、前述した通り\(a^x=t\)などとすると、\(t>0\)となる点に注意が必要です。
例５．\(4^x-3\cdot 2^x -4 = 0 \)
\(4^x = (2^2)^x=(2^x)^2\)とみなすと\(2^x = t\)と置き換えることができます。
（解答）
\(4^x-3\cdot 2^x -4 = 0 \)
\((2^x)^2 -3 \cdot 2^x -4 = 0\)
\(2^x = t\)と置くと、\(t>0\)。このとき、
\(t^2 -3t -4=0\)となる。
\( (t+1)(t-4)\)
\( t=-1, 4\)
\(t>0\)より\(t=4\)。（←ここがポイント）
よって\(2^x = 4\)より、\(x=2\)…（答）
与えられた式によっては指数の定数部分を引っ張り出す、という操作が必要になることもあります。
たろぅ？（日本語シャベッテクダサイ）
せんせ具体例を見たらわかりますよ。
例６．\(\displaystyle \Big( \frac{1}{9} \Big)^x – \Big( \frac{1}{3} \Big) ^{x-1} – 54 = 0 \)
問題は\(\displaystyle \Big( \frac{1}{3} \Big) ^{x-1}\)の部分ですね。
最初の\(\displaystyle \Big( \frac{1}{9} \Big)^x\)を見れば\(\displaystyle \Big( \frac{1}{3} \Big)^x=t\)と置けばよさそうですが\(\displaystyle \Big( \frac{1}{3} \Big) ^{x-1}\)は\(x-1\)乗なので、そのまま置き換えることができません…。
（解答）
\(\displaystyle \Big( \frac{1}{9} \Big)^x – \Big( \frac{1}{3} \Big) ^{x-1} – 54 = 0 \)
\(\displaystyle \Big\{ \Big( \frac{1}{3} \Big)^x \Big\}^2 – \Big( \frac{1}{3} \Big) ^{-1}\Big( \frac{1}{3} \Big) ^{x} – 54 = 0 \)（←指数法則を使って\(-1\)乗の部分だけ引き出した）
\(\displaystyle \Big\{ \Big( \frac{1}{3} \Big)^x \Big\}^2 -3\Big( \frac{1}{3} \Big) ^{x} – 54 = 0 \)（←\(\displaystyle \Big( \frac{1}{3} \Big) ^{-1}=3\) ）
\(\displaystyle \Big( \frac{1}{3} \Big) ^{x}=t\)とおくと、\(t>0\)。このとき、
\(t^2 -3t -54=0\)となる。
\( (t+6)(t-9) = 0\)
\( t= -6, 9\)
\(t > 0\)より\(t=9\)。
\(\displaystyle \Big( \frac{1}{3} \Big)^x = 9\)
\(\displaystyle ( 3^{-1} )^x = 3^2\)
\(3^{-x} = 3^2\)
よって\(-x = 2\)。\(x=-2\)…（答）
「指数法則を使って\(-1\)乗の部分だけ引き出した」の部分の説明
指数法則の一つに、
\( a^p \times a^q = a^{p+q}\)
というものがあります。
つまり、\(p\)乗×\(q\)乗は指数部分を\(p+q\)にすればOK、というものです。
これを逆に使います。逆に考えると、
指数部分の\(p+q\)は\(p\)乗×\(q\)乗に直せる、ということです。
ということで、
\(\displaystyle \Big( \frac{1}{3} \Big) ^{x-1}=\Big( \frac{1}{3} \Big) ^{x+(-1)}=\Big( \frac{1}{3} \Big) ^{-1} \times \Big( \frac{1}{3} \Big) ^{x} \)
として、\(-1\)乗の部分だけ引っ張り出すことができるんですね。
せんせ置き換えるために余計な指数の定数部分、今回で言えば\(-1\)乗の部分を引っ張り出す必要がある、ということですね。
たろぅなるほど…。
指数不等式を解く
変形の方法などは指数方程式と同じですが、最後
底を揃えて指数比較をする際に底が１より大きいか？小さいか？を言う必要があります。これが指数不等式を解く際の記述上の（実際に正しく解くためにも）最大のポイントになります。
せんせこれが、冒頭の写真の話ですね。
つまり、葉っぱが増えてるタイミングなのか？減っているタイミングなのか？で、どっちが新しい写真か話が変わってくるのと同じです。
コチラの記事でも説明しましたが、もう少し具体的に言うと、
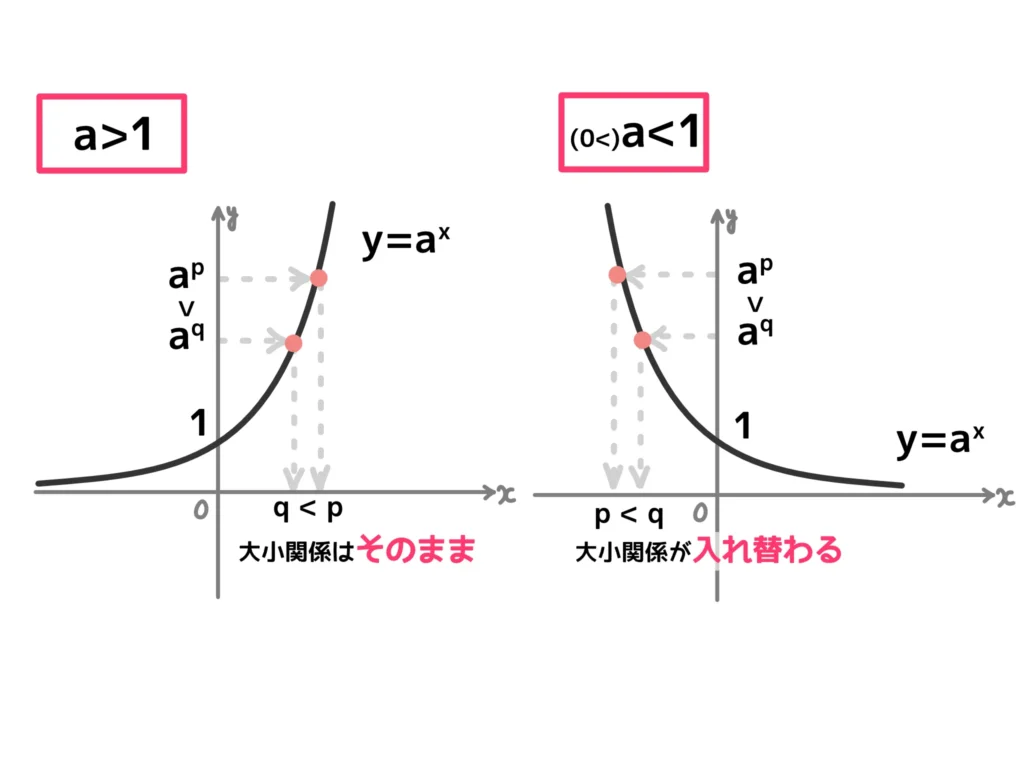
\(a^p > a^q\)という不等式が与えられた場合、指数部分\(p\)、\(q\)の大小関係が
「そのまま\(p>q\)」となるか？「ひっくり返って\(p < q\)」となるか？は
底\(a\)が\(a>1\)なのか\(0 < a < 1\)なのかによるという点に注意しないといけません。
たろぅやっぱりよくわかんない…
せんせこれも具体例を見たらわかりますよ。
最初の例題をもう一度見てみましょう！
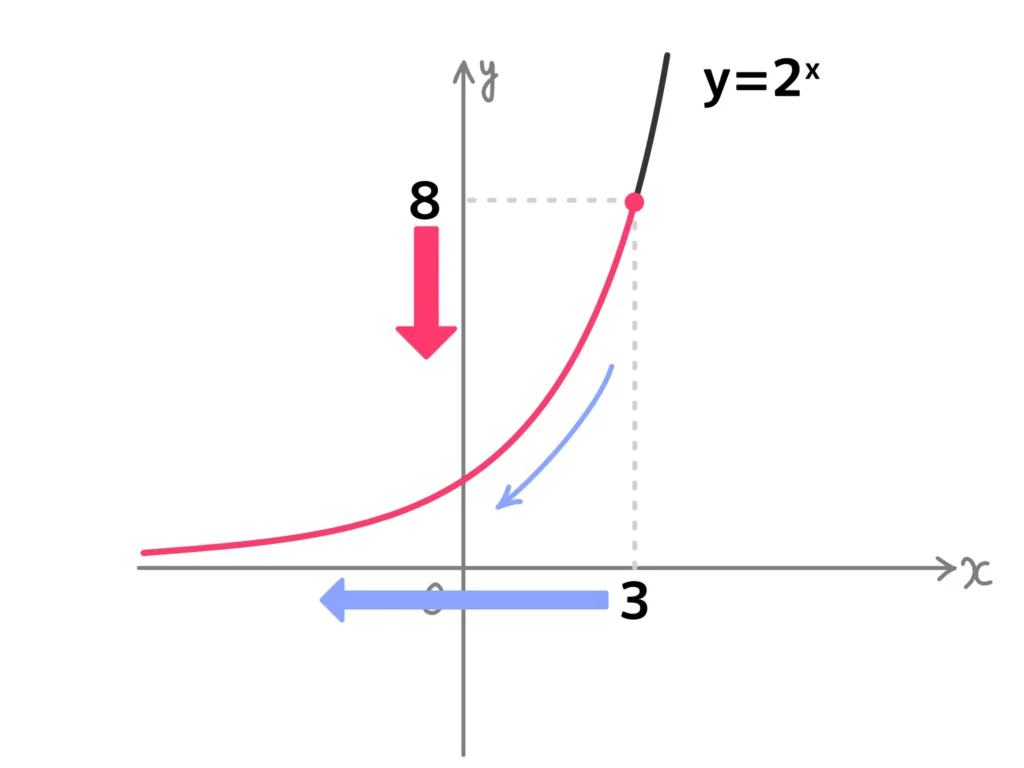
例２（再掲）．\(2^x < 8\)
（解答）
\(2^x < 8\)
\(2^x < 2^3\)
底2は1よりも大きいので…（ここがポイント！）
\(x < 3\)…（答）（不等号の向きはそのまま）
せんせでは、こちらの問題はどうでしょう？
例７．\(\displaystyle \Big( \frac{1}{2} \Big) ^x < \frac{1}{8}\)
（解答）
\(\displaystyle \Big( \frac{1}{2} \Big) ^x < \frac{1}{8}\)
\(\displaystyle \Big( \frac{1}{2} \Big) ^x < \Big( \frac{1}{2} \Big)^3\)
底\(\displaystyle \frac{1}{2}\)は1よりも小さいので…（ここがポイント！）
\(x > 3\)…（答）（不等号の向きを入れ替える）
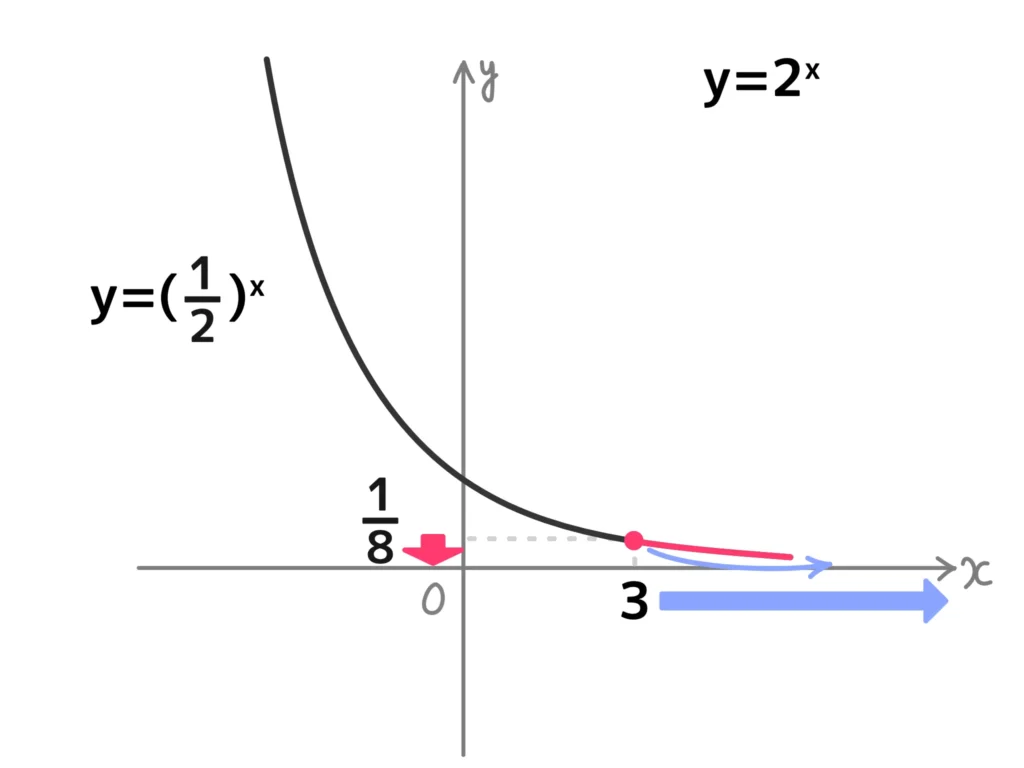
せんせ例２とほぼ同じ問題ですが、底\(\displaystyle \frac{1}{2}\)が1よりも小さいので、不等号の結果が逆になってますね。
たろぅなるほど…底が１よりも大きいか？小さいか？によって指数比較のときに不等号がそのままか？入れ替わるか？が決まるのか…。
答えの不等号の向きも入れ替わるかもしれませんし、なにより適切なタイミングで底が1より大きいか？小さいか？を記述することが重要です。
底を揃えて指数部分を比較する際、底が１より大きいか小さいかを必ず言う。
・底が１より大きい場合→不等号の向きはそのまま
・底が１より小さい場合→不等号の向きを入れ替える
ちょっと複雑な指数不等式を解いてみよう
ここまで理解できていれば、複雑な指数不等式になってもコツは同じです。
例８．\(\displaystyle 8 \Big( \frac{1}{4} \Big)^x -6 \Big( \frac{1}{2} \Big) ^x +1 < 0\)
（解答）
\(\displaystyle 8 \Big( \frac{1}{4} \Big)^x -6 \Big( \frac{1}{2} \Big) ^x +1 < 0\)より
\(\displaystyle 8 \Big\{ \Big( \frac{1}{2} \Big)^x \Big\}^2 -6 \Big( \frac{1}{2} \Big) ^x +1 < 0\)
\(\displaystyle \Big( \frac{1}{2} \Big)^x = t\)とおくと、\(t>0\)…※。このとき、
\( 8 t^2 -6t + 1 <0\)
\( (4t-1)(2t-1) < 0\)
\(\displaystyle \frac{1}{4} < t < \frac{1}{2}\)（※を満たす）
\(\displaystyle \Big( \frac{1}{2} \Big)^2 < \Big( \frac{1}{2} \Big)^x < \Big( \frac{1}{2} \Big)^1 \)
底\(\displaystyle \frac{1}{2}\)は1よりも小さいので、\(2 > x > 1\)。
\(1 < x < 2\)…（答）
超おまけ．指数不等式で質問が多い部分
せんせここは、超おまけです。指数不等式の問題を解くときによくある模範解答と、それに関するよくある質問について説明します。
例９．\(4^x – 4 \cdot 2^x -32 >0 \)
（解答）
\(4^x – 4 \cdot 2^x -32 <0 \)
\( (2^x)^2 – 4 \cdot 2^x -32 <0 \)
\(2^x=t\)とおくと、\(t>0\)。このとき、
\(t^2-4t-32<0\)
\( (t+4)(t-8)<0\)
\( t+4>0\)であるから\(t-8<0\)。←ここの質問が多い
\(t<8\)
\(2^x<2^3\)
底\(2\)は1より大きいので\(x<3\)
「ここの質問が多い」の部分がよくわかんない人
\( (A)\times(B) <0 \)
のタイプの不等式を解く場合、不等式の意味を考えると「\( A\)掛ける\(B\)が0より小さい（負）」ということです。
ということは、パターンとしては
「\(A>0\)かつ\(B<0\)」（Aが正でBが負）か、
「\(A<0\)かつ\(B>0\)」（Aが負でBが正）のどちらか、です。
今回、「\( (t+4)(t-8)<0\)で\(t+4 > 0\)」という情報まであるので、「\(A>0\)かつ\(B<0\)」のパターンであることがわかります。
つまり、\(t-8 < 0\)ということがわかるのです。
ちなみに…の話①
普通に二次不等式として
\( (t+4)(t-8)<0\)より\(-4<t<8\)なので、\(t>0\)より\(0<t<8\)
と解いても全く問題はありません。
ありませんが…このあと
\(0<t<8\)より\(0<2^x <2^3\)。よって\(x<3\)。
という解答の流れになります。ここで、「\(0 < 2^x\)」はどこにいった？という話をするのが面倒なんだと思います。
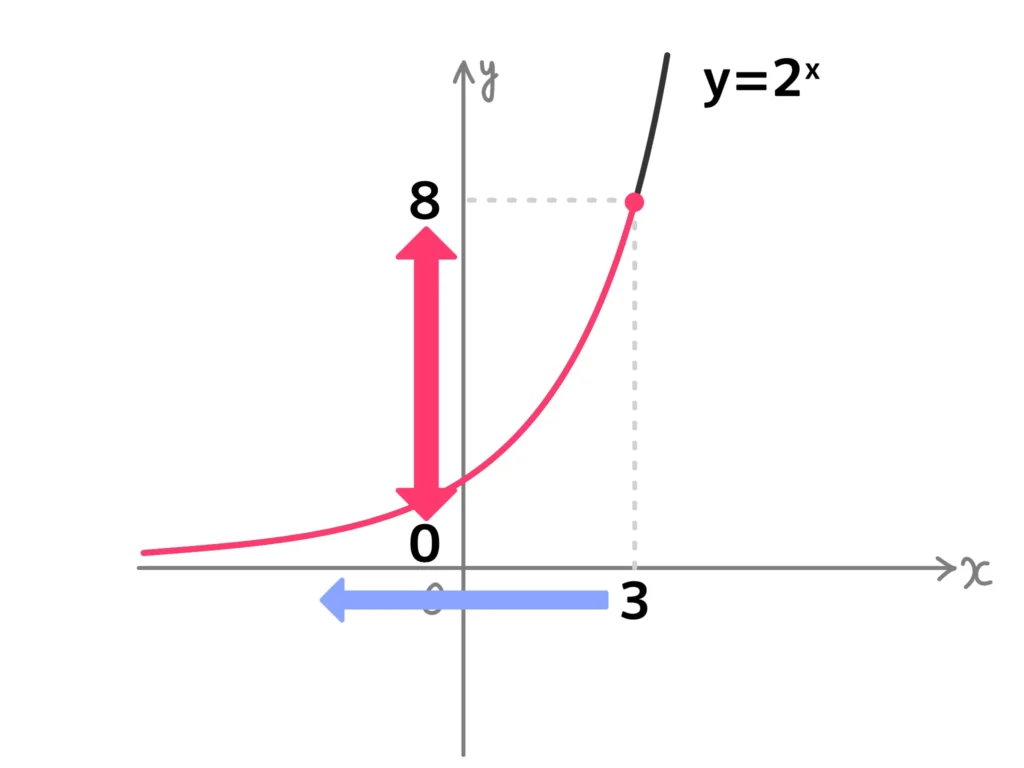
グラフで考えれば\(0 < 2^x\)は考える必要がなく、\(x<3\)であれば、ずーっと\(0 < 2^x\)を満たすことがわかります。
せんせでも、例９の解答の「\(t<8\)より\(2^x<2^3\)。よって\(x<3\)」も、ちゃんと考える人は「\(t>0\)はどこにいった？」となるので、結局誤魔化してる感があります…。
ちなみに…の話②
\( (A)\times(B) >0 \)や\( (A)\times(B) <0 \)の不等式を解くとき、
「掛けて正→どちらも正かどちらも負」や「掛けて負→どちらか正でどちらか負」
という考え方は、図形と方程式の領域図示や三角関数の不等式を解く際にも使うので、この理屈は押さえておいてください。
指数方程式・不等式の練習問題
練習問題8-4【No.39】
問．次の方程式・不等式を解け。
(1) \( 25^x -4 \cdot 5^{x+1} -125 =0 \)
(2) \( 3 ^{2x} -4 \cdot 3^{x+1} + 27 < 0\)
(3) \(\displaystyle \Big( \frac{1}{4} \Big)^x -3 \cdot \Big( \frac{1}{2} \Big)^x -4 > 0 \)
答え
(1) \(x=2\)
(2) \(1 < x < 2\)
(3) \(x < -2 \)
練習問題8-4【No.40】
問．\( x > 1\)とする。\(x\)に関する不等式\(\displaystyle 0 < \sin{ \Big( \frac{1}{2} \Big) ^x \pi }< \frac{1}{\sqrt{2}} \)を解け。
答え
\( x > 2\)
指数方程式・不等式まとめ
指数方程式・不等式の解き方についてでした。
特に不等式は底が1より大きいか、小さいかによって不等号の向きが変わるので注意してください。
ちょっと一息
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
また、このブログで活躍してるクマのLINEスタンプも販売しています！ぜひ一度見てみてください！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
