PR
統計的な推測って?「推定」と「標本」について丁寧に解説

統計学の重要な側面の一つに「推測統計学」というものがあります。
これは、集団全てのデータを取るのが難しいときに、一部のサンプル(標本)を取って、そのデータから元の集団(母集団)の特徴を推測する、という手法です。
その推測統計学の手法は、さらに「推定」と「検定」に分かれます。
この記事では推測統計学の「推定」と、推定に必要な「標本」について説明していきます。
 せんせ
せんせ今回は用語などをサクッと解説していきます!
「推定」って?



ははぁ…ふーん…なるほどね…。



ん?どしたの?



この「3個入りギガジャンボドーナッツ」、どんだけ重いんだろ?と思って測ってみたら、なんと、ドーナッツ1個の重さが全部150gちょうどなんだよね。



へー…でかいわね。



ということは、この「3個入りギガジャンボドーナッツ」は全部150gちょうどなんだ!絶対そうだ!



たまたま3個同じ重さだっただけで、「全部150gちょうど」というのは違うと思う。



えー…、言い方厳しい…。
ということで統計学の「推定」のお話です。
世の中のデータは、全て調べるのが難しいものもあります。例えば、今回の「3個入りギガジャンボドーナッツ」、全てのドーナッツの重さを測るのは不可能ですよね?



工場のドーナッツの重さ全部測るのか?っていう話ですよ。
このように、全てのデータを取るのが現実的ではないとき、その集団(母集団)からサンプル(標本)を取って、そのサンプルの特徴を調べることで元の集団の特徴を推測します。
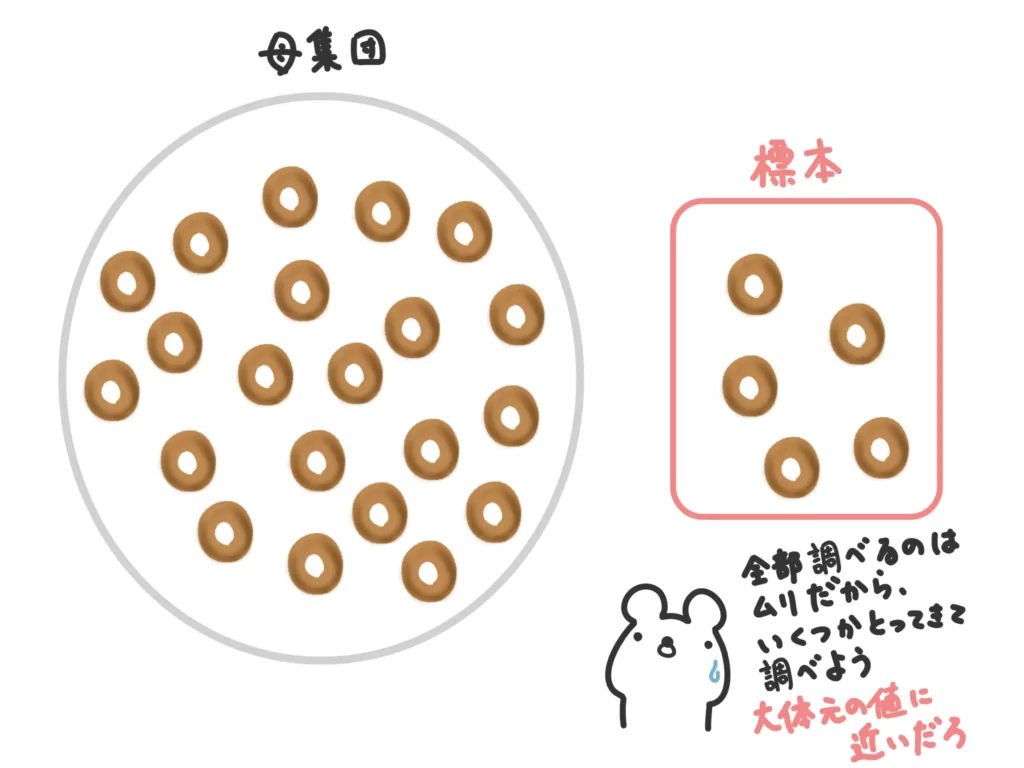

母集団の平均と標準偏差を母平均、母標準偏差といい、\(\mu\)、\(\sigma ^2\)と表します。(高校の教科書なんかでは、母平均を\(m\)と書いてあることもあります。)
この母平均、母標準偏差を直接計算することは難しいので、標本を抽出してその特徴から推定します。
標本について
母集団から標本を取ってくる方法についても、色々な方法があります。
また、用語がゴチャゴチャとして間違えやすいので注意しましょう!



考え方自体は難しくないです!用語の整理だけきっちりやっておきましょう!
標本の抽出方法について
ちょっと想像すればわかると思いますが、標本を抽出する際に偏りがあったらマズイです。



うお!この「3個入りギガジャンボドーナッツ」、10袋連続で重さが軽いぞ!平均140gしかない!!
やっぱり重さの平均は140g程度だったんだ!



…それ、全部同じ日に作られたやつじゃない?



…アレ?
このようなデータが得られたとしても「このドーナッツの重さはやはり軽かった!140g!」とは言いにくいですよね?「その日に何か機械の不具合でもあったのかなぁ?」と想像する方が自然です。
このように、何かの理由によるデータの偏りを避けるため、標本はランダムに抽出していきます。
これを単純無作為抽出といいます。



乱数表や乱数賽(さい)を使うらしいですが…今どき実際に乱数表とか乱数賽とか使うんでしょうか?誰か、知ってたら教えてください。
また、標本の抽出方法には「復元抽出法」と「非復元抽出法」があります。
- 復元抽出法:個体を抽出したあと、毎回元に戻して次の抽出する。
- 非復元抽出法:個体を抽出した後、戻さないで次の抽出をする。



このあたりの抽出方法は「まぁ、こういうやりかたがあるんだな」くらいでいいと思います。重要なのはランダムに抽出する、というところですね。
ちなみに、統計検定ではもう少し詳しく抽出方法を勉強します。
統計検定用の詳しい抽出方法
ランダムに抽出というのが難しい(大変な)ケースもありますし、完全にランダムに抽出することで母集団の特徴が失われる可能性もあります。



ということで、完全ランダムという抽出ではなく、効率的に抽出したり、母集団の特徴を失わないように抽出する方法があります。
【層化抽出法】
母集団をいくつかの層(グループ)に分けておき、各層から必要なサンプルをランダムに抽出する方法。
例えば、「3個入りギガジャンボドーナッツ」のうち、一つはチョコかけドーナッツだったとしましょう。
そこから30個のドーナッツを抽出する場合、完全にランダムに抽出するのではなく、
(普通のドーナッツ):(チョコかけドーナッツ)=2:1=20個:10個
ずつ抽出する方が、母集団の特徴をとらえてますよね。
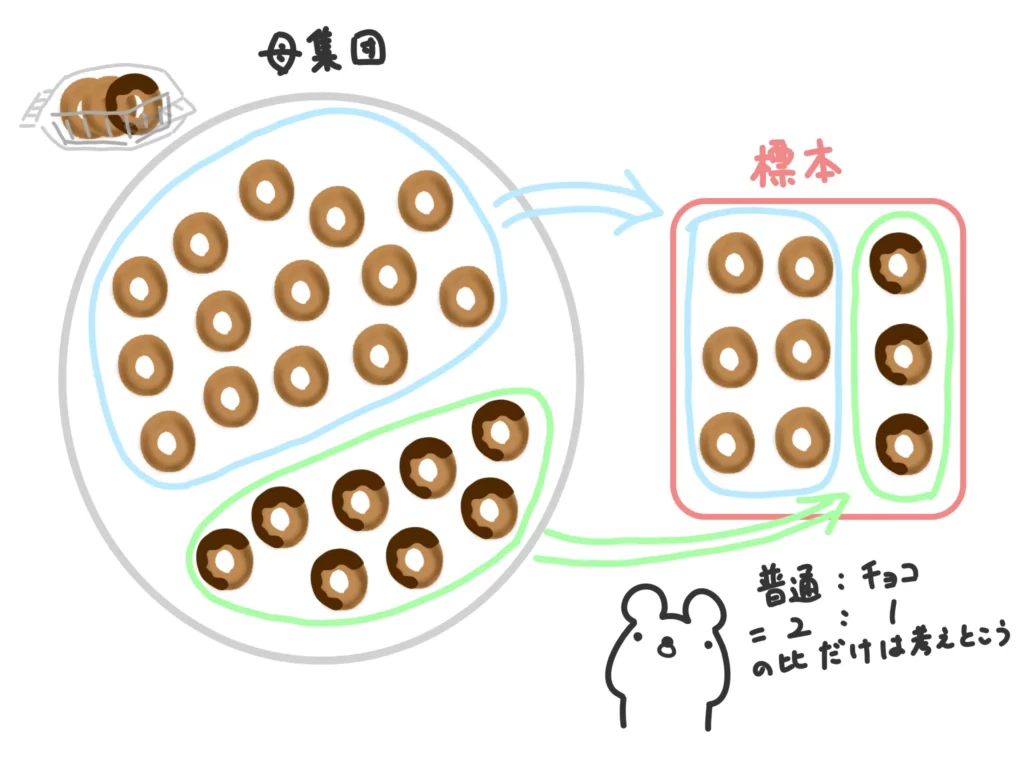

母集団の特徴を上手くとらえられる代わりに、母集団の特性があらかじめわかっていないとこの手法は使えません。
【クラスター抽出法】
母集団を小さな集団(クラスター)に分けて、その中からクラスターをランダムに抽出し、このクラスターの全数を調査する方法。
例えば、「3個入りギガジャンボドーナッツ」から30個抽出するとしましょう。
完全に袋まで開けてしまって、全てのドーナッツを完全に公平な状態にして30個ランダムに抽出するのが普通の抽出方法(単純無作為抽出)です。
ただ、ドーナッツ全てに通し番号をつけないといけない、など手間も大きいです。
そこで例えば、袋(クラスター)を開けず、10袋をランダムに抽出して、その30個を調査するという方法をとります。
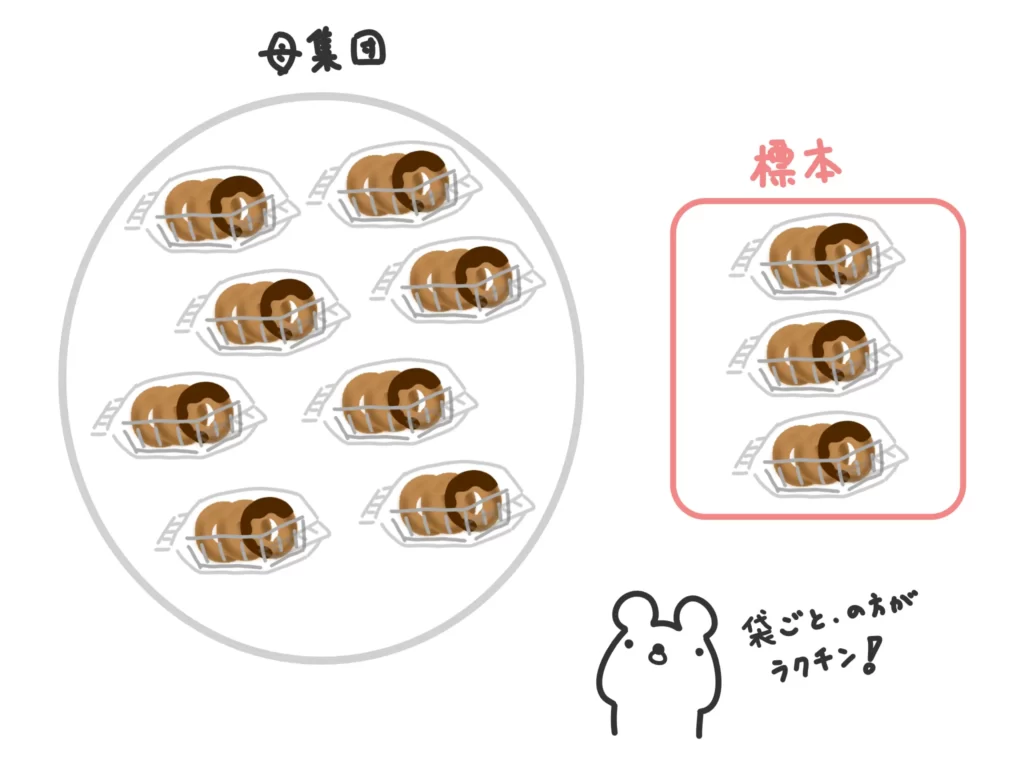

抽出しやすい反面、クラスター内の状況によっては偏りが生じやすいです。
【多段抽出法】
母集団を小さな集団に分けてランダムで選び、その中からさらに小さな集団に分けてランダムに選び…という操作を繰り返す方法。
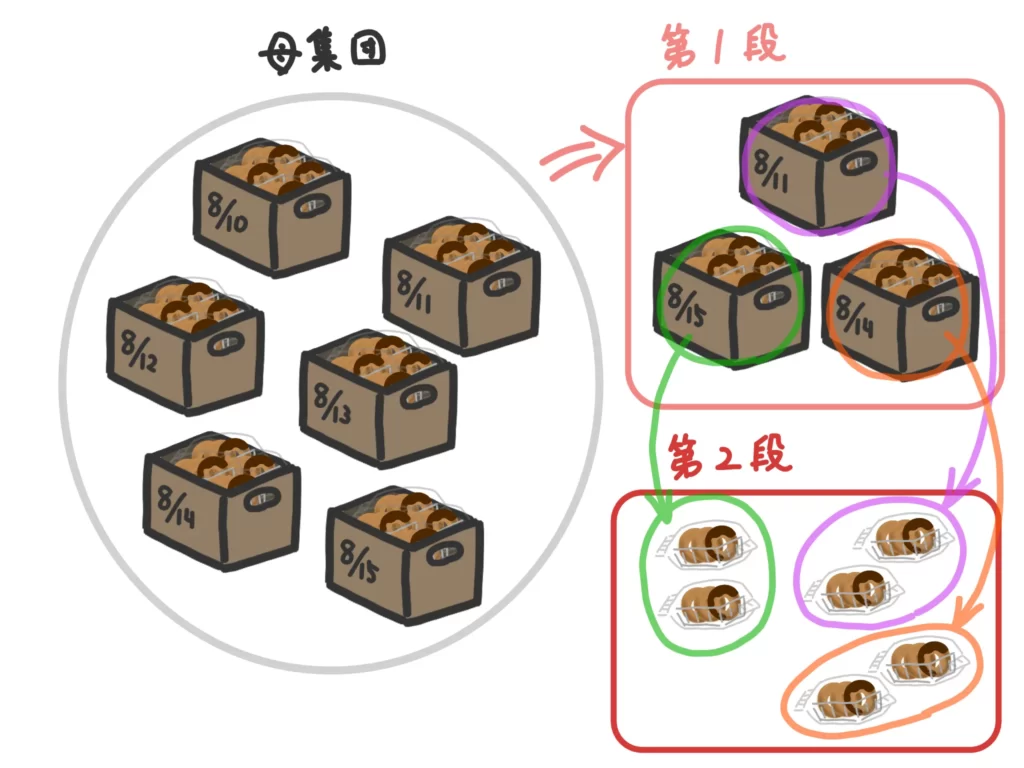

抽出しやすい反面、標本のサイズが小さかったら偏りが生じやすいです。
【系統抽出法】
標本に通し番号を付けて、1番目をランダムに選んだあと、一定間隔で抽出する方法。
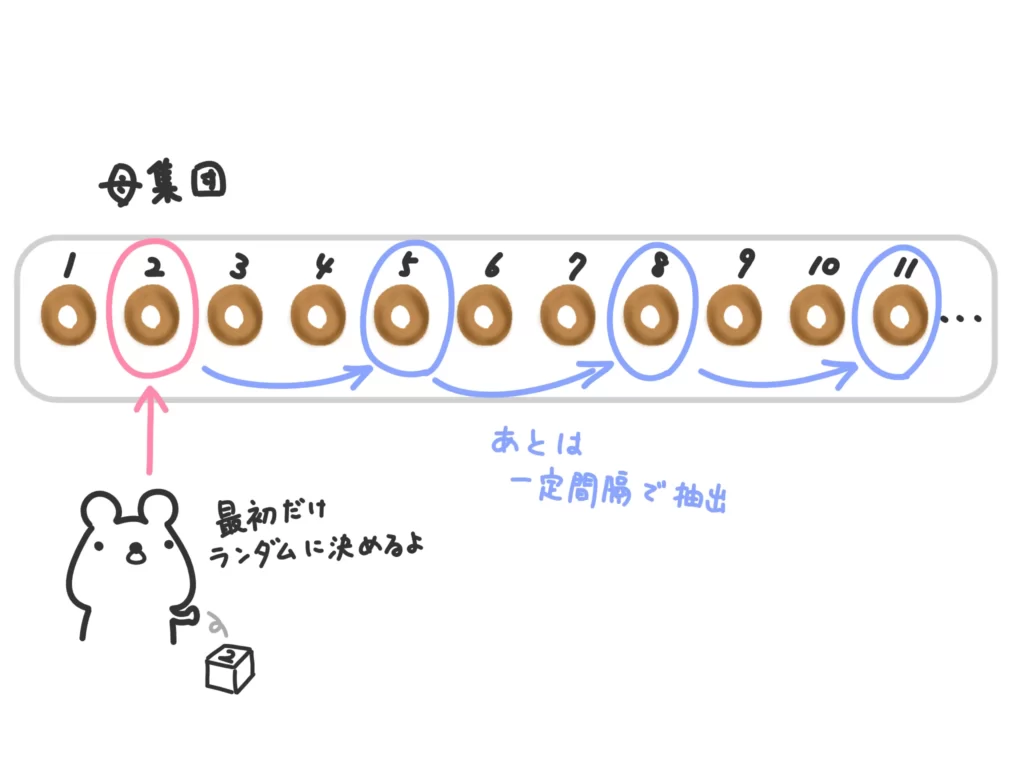

抽出しやすい反面、標本に周期性がある場合偏りが生じやすいです。
標本に関する用語など



この辺の用語はちょっと紛らわしいものが多いです。
推定を何度もやってみれば、ちょっとずつ用語が定着していきますので、少しずつ、でも確実に用語を押さえていきましょう!
さて、では標本を抽出していきますが、まず、標本は何セットか抽出することがあります。
1セットしか抽出しなくても、「たまたまその1セットが抽出されただけで、次に同じやり方で抽出したらまた別の標本が抽出されるよね。」という意識は必要です。



よし、「3個入りギガジャンボドーナッツ」から30個標本を抽出するけど、これを10回繰り返そう!
このとき、一回の標本の数「30」を「標本の大きさorサンプルサイズ」といいます。また、10回、という数を「標本数orサンプル数」といいます。
また、標本から計算した平均を標本平均、標本から計算した分散のことを標本分散といいます。



さて…ここから母集団と標本のそれぞれの統計量(平均とか分散とか)の関係や違い、何を推定したいのか?などが結構ごちゃごちゃになってきます。図を使いながらちょっと丁寧にまとめていきます!
基本的な母集団と標本の統計量の関係



まずは平均の話です!
母集団から標本を取ってくるとき、その標本平均には「ばらつき」がでてきます。どの個体を取ってくるか?によるので当然ですね。
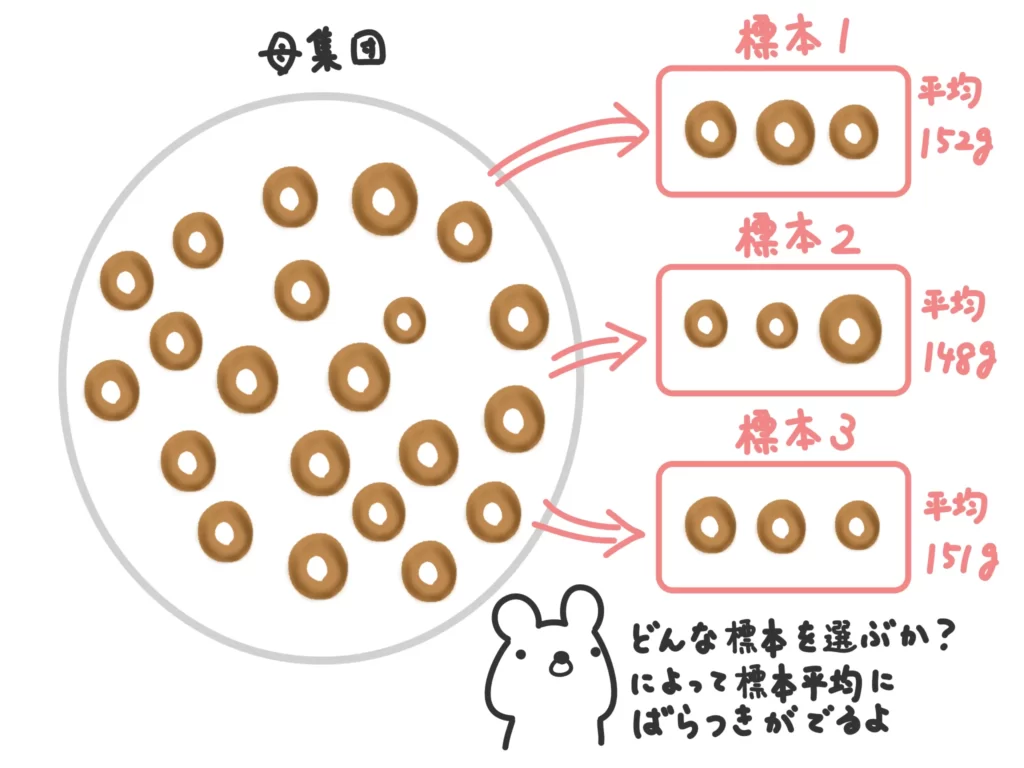

母集団のばらつきが大きい(母分散が大きい)ほど、標本平均のばらつきも大きくなりますよね。
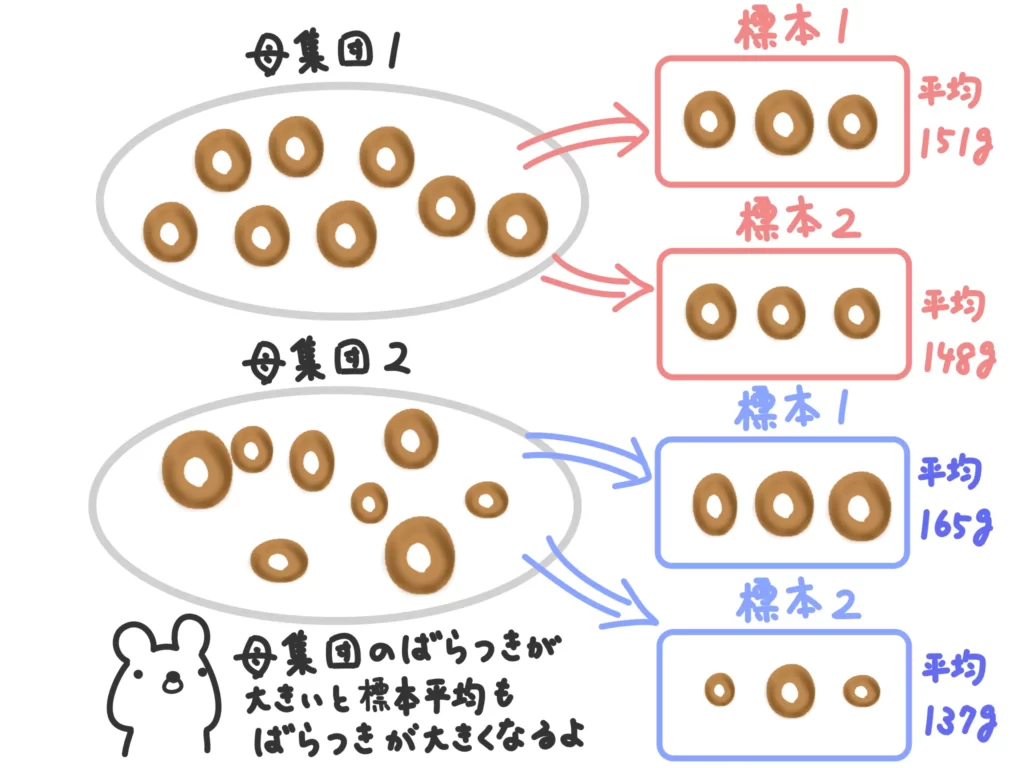

そこで、標本を取ってきたときにその標本平均がとり得る値の期待値や、その標本平均にどれだけばらつきがあるか?つまり標本平均の分散を検討します。



標本平均は標本を取るたびに変わってきます。つまり、その標本平均の値が取りうる期待値と、値がどれくらいばらつく可能性があるのか?の分散が一つの指標になります。
標本平均の期待値と分散は次のようになります。
標本平均の期待値と分散
母集団の平均(母平均)を\(\mu\)、分散(母分散)を\(\sigma ^2\)とすると、標本平均\(\bar{x}\)の期待値\(E(\bar{x})\)、分散\(V(\bar{x})\)は
\(E(\bar{x})=\mu \)
\(\displaystyle V(\bar{x})= \frac{\sigma ^2}{n}\)
ただし、\(n\)は標本のサンプルサイズで、復元抽出で抽出するとする。



標本平均の値が取り得る期待値は母平均\(\mu\)と一致して、標本平均のばらつき(分散)は母分散を\(n\)で割った\(\displaystyle \frac{\sigma ^2}{n}\)になります。サンプルサイズが大きくなれば標本平均のばらつきは小さくなる、というのは感覚的にもわかりやすいですよね。
(証明)
標本平均\(\displaystyle \bar{x}=\frac{x_1 + x_2 + \cdots + x_n}{n} \)について、
突然ですが、例えば\(x_1\)の期待値\(E(x_1)\)、分散\(V(x_1)\)は、母集団から1つの個体を取り出すときの期待値、分散なので、母平均と母分散と一致します。
つまり\(E(x_1)=\mu \)、\(V(x_1)=\sigma ^2 \)になります。
\(x_2\)、…、\(x_n\)についても同様なので、
\(E(x_2)=\cdots=E(x_n)=\mu \)、\(V(x_2)=\cdots=V(x_n)= \sigma ^2 \)。
よって、
\(\displaystyle E(\bar{x}) = E(\frac{x_1 + \cdots + x_n}{n}) \)
\(\displaystyle \quad = \frac{1}{n} \{ E(x_1) + \cdots + E(x_n) \} \)(←確率変数の変換と確率変数の和の期待値)
\(\displaystyle \quad = \frac{1}{n} \{ \mu + \cdots + \mu \} = \frac{1}{n}\cdot n \mu = \mu \)
\(\displaystyle V(\bar{x}) = V(\frac{x_1 + \cdots + x_n}{n}) \)
\(\displaystyle \quad = \frac{1}{n^2} \{ V(x_1) + \cdots + V(x_n) \} \)(←確率変数の変換と確率変数の和の分散)
\(\displaystyle \quad = \frac{1}{n^2} \{ \sigma ^2 + \cdots + \sigma ^2 \} = \frac{1}{n^2}\cdot n \sigma^2 = \frac{\sigma ^2}{n} \)
じゃあ標本分散は?
実は標本分散というのはそのままでは使えません。
これは、標本分散が不偏性という性質をもっていないからです。
このあたりはこちらの記事で解説しているので見てみてください。


まとめ
母集団を推定するための標本と、その統計量の関係についての説明でした。
基本的なことなのですが、意外と丁寧に説明されている教科書やサイトがあまりなく、最初何を言っているかわかりにくいので、理解の手助けになれば、と思います。