PR
行列式ってなに？公式による計算方法と意味を説明！
行列の重要な要素として行列式、というものがあります。
この行列式、求め方はともかく、
たろぅ行列式の値は出せるけど…そもそも、ちょっとなにしてるかわかんない…。
となりがちです。
この記事では、行列式の求め方から、その意味まで解説していきます。
このブログで活躍してるクマのLINEスタンプもあります！
目次
行列式の求め方
まず書き方ですが、行列\(A\)に対して、行列式を\(|A|\)や\(detA\)（ディターミナントエー）と書きます。
では、行列式の求め方を説明していきましょう！
せんせこれはまぁ、ただの公式確認ですね。
サクッと確認していきましょう。
２次の正方行列の行列式
２次の正方行列の行列式
２次の正方行列\(A= \begin{pmatrix} a & b \\ c & d \end{pmatrix}\)について、行列式\(|A|\)は
\(|A|=ad-bc\)
で計算できる。
例．\(A= \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)の行列式\(|A|\)を求めよ。
（解答）
\(|A| = 1 \cdot 4 – 2 \cdot 3 = -2\)…（答）
せんせ\(|A|\)は絶対値ではないので、当然マイナスになることもあります。
３次の正方行列の行列式
３次の正方行列の行列式
３次の正方行列\(A= \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\)について、行列式\(|A|\)は
\(|A|=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\)
\(\quad\quad -a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}\)
で計算できる。
こんな感じで、図で押さえるといいですね。これをサラスの公式といいます。
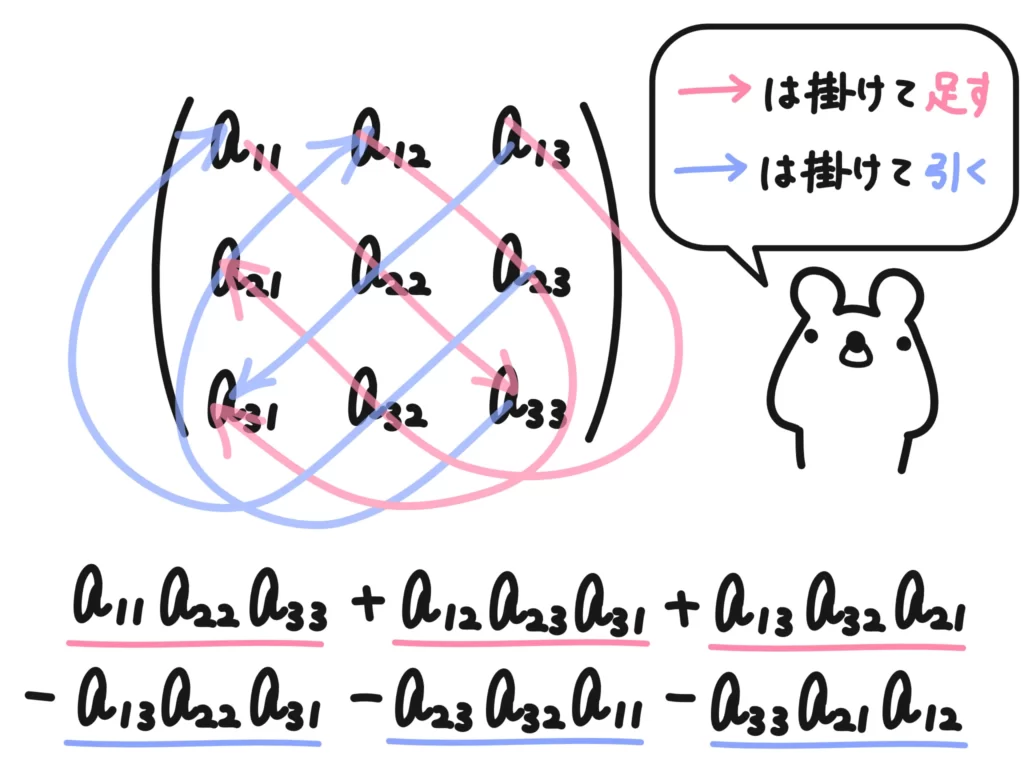
例．\(A= \begin{pmatrix} 1 & 1 & -2 \\ -1 & 3 & 0 \\ 2 & 3 & 1 \end{pmatrix}\)の行列式\(|A|\)を求めよ。
（解答）
\(|A|=1 \cdot 3 \cdot 1 + 1 \cdot 0 \cdot 2 + (-2) \cdot 3 \cdot (-1) \)
\(\quad\quad -(-2) \cdot 3 \cdot 2 – 0 \cdot 3 \cdot 1 – 1 \cdot (-1) \cdot 1=22\)
４次以上の正方行列の行列式
４次以上の正方行列の行列式を求めるのは結構大変です。
せんせ一応定義を載せておきますが…正直この定義通りに計算するのは現実的ではありません。
\(n\)次の正方行列の行列式
行列\(A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}\)
の行列式\(|A|\)は、
\(|A|=\sum sgn\begin{pmatrix} 1 & 2 & \cdots & n \\i_1 & i_2 & \cdots & i_n \end{pmatrix} a_{1i_1}a_{2i_2} \cdots a_{ni_n}\)
で計算できる。
たろぅ（帰ろう…。）
…という声が聞こえてきそうです。
帰らなくていいので、とりあえずここは読み飛ばして次にいってほしいです。
せんせこの定義による計算はかなりハードです。一応説明はしますが、読み飛ばしてもOKです。具体例を出して計算するつもりもありません。
読み飛ばしてくれて構いませんが、一応ここから一つずつ説明をしていきます。
せんせ読み飛ばしてもいいんですよ？
- まず、この式は\(\sum\)なので、どんどん和を計算していく、という意味になります。
添字を見てくれたらわかりますが、\(a_{1i_1}a_{2i_2} \cdots a_{ni_n}\)の添字の左側は1,2,…,nとなっており、固定されています。
これに対して、添字の右側は\(i_1, i_2, \cdots , i_n\)となっています。これは、右側の添字は1,2,…,nの全ての並べ方のパターンを考えてください、という意味です。
せんせつまり、この\(\sum\)は、「左側の固定された添字1,2,…,n」に対して「右側の添字1,2,…,nの全ての並べ方」のパターンを全部足してね、という意味です。右側の添字の並べ方は\(n!\)パターンあるので、４次だと4!=24個、５次だと5!=120個のパターンを足さないといけません…。
- \( \begin{pmatrix} 1 & 2 & \cdots & n \\i_1 & i_2 & \cdots & i_n \end{pmatrix} \)は置換と呼ばれるものです。
置換の説明は割愛します。
概要としては、上の1,2,…,nに対して下の\(i_1, i_2, \cdots , i_n\)（実際は①の順番と同じ順番で1,2,…,nを並べ替えたもの）の並べ方によって、偶置換、奇置換という２種類に分けられる、と思ってください。
- \(sgn\)は偶置換なら「＋1」になり、奇置換なら「ー1」になる、という意味で、符号（プラスマイナス）を決定する記号だと思ってください。
つまり、ごちゃごちゃ書きましたが、\(sgn\begin{pmatrix} 1 & 2 & \cdots & n \\i_1 & i_2 & \cdots & i_n \end{pmatrix} \)の部分は「\(i_1, i_2, \cdots , i_n\)の並べ方によって、＋1かー1になるよ〜」というだけです。
以上から、この定義のおおまかな説明としては、
「\(a_{1i_1}a_{2i_2} \cdots a_{ni_n}\)の右側の添字をどんどん変えながら、そして、その変え方によって符号（プラスマイナス）を決定しながら足していく」
という感じです。
せんせ（具体例を出して計算するのが面倒なので、これで説明した、という雰囲気にしておきます。スイマセン。）
次数が上がると手で計算するのは現実的でなくなってきます。ギリギリ４次くらいまででしょうか…。しかもイチイチ偶置換、奇置換を判定して符号を決めるのは大変です…。想像するだけで気が遠くなりますね。
実際には「余因子展開」というテクニックを使って計算もできますが、これも多少計算は楽になりますが、焼石に水。
せんせ結論「４次以上の行列式は計算が大変」。
で？行列式って？
行列式は、その行列の特徴を示す指標です。
せんせ具体的にどのような指標なのか？について説明していきます！
逆行列を求める
普通の数（スカラー）でいうところの、逆数に相当する「逆行列」を求める際に使います。逆行列の具体的な求め方についてはこちらの記事をご覧ください。
あわせて読みたい
逆行列は行列の割り算!?２次の逆行列の求め方と意味を丁寧に説明
逆行列は普通の数でいうところの逆数に相当します。 逆行列を掛けることは、普通の数で言うと「割り算」をすることになるので、とても大事な操作なのですが、この逆行列…
逆行列は、演算でいうと割り算の役割になるので、さまざまな式変形ができるようになります。ですので、行列式を使って逆行列を求めることは、かなり重要な操作になります。
また、行列式は「\(|A| \neq 0\)ならば逆行列が存在して、\(|A|=0\)ならば逆行列が存在しない」という、逆行列の存在判定をする際にも使うことができます。
行列による変換の拡大倍率
行列の積は、実は「ベクトルの変換」ととらえることもできます。
そして、その行列式には変換の拡大倍率という意味もあります。この変換の拡大倍率のイメージは、解析のヤコビアンなどでも使います。
詳しくはこちらの記事をご覧ください。
あわせて読みたい
行列はベクトルの変換に使える？行列の積が持つもう一つの側面
行列に行列を掛けると、計算結果として新たな行列が現れます。 このときに新たに現れる行列は、実は元の行列を変換したもの、とみなすことができるのです！ 行列の掛け…
連立一次方程式が解けるかどうか？
突然ですが、連立１次方程式は解ける場合もあるし、解けない場合もあります。
例えば、
\( \left\{ \begin{array}{l} x+y=4 \\ 2x+2y=5 \end{array} \right.\)
なんかは実は解くことができません。
高校までの問題では、解けない問題を出すことの方が少ないのですが、そもそも解けるかどうか？を考えることも重要です。
このとき、係数を抜き出した行列を係数行列\(A=\begin{pmatrix} 1 & 1 \\ 2 & 2 \end{pmatrix}\)、\(x,y\)を行列\(\boldsymbol{x}＝\begin{pmatrix} x \\ y \end{pmatrix}\)、右辺を\(\boldsymbol{b}=\begin{pmatrix} 4 \\ 5 \end{pmatrix}\)とすると、連立方程式は
\(A\boldsymbol{x}=\boldsymbol{b}\) …（※）
と表せます。
せんせ行列の積の計算にしたがって計算してみてください。連立方程式の２つの式が出てくるはずです。
ここで、連立方程式の解を求める、ということは、\(\boldsymbol{x}\)を求めればよいので、（※）を\(\boldsymbol{x}=\begin{pmatrix} x \\ y \end{pmatrix}=\cdots\)の形にすればよい、ということになります。
そこで、一番簡単な方法は、（※）の左から\(A^{-1}\)を掛けることです。
\(A^{-1}\)を掛けることができたら、\(\boldsymbol{x}\)は一意に決まる（＝この連立方程式が解ける）ということになります。（\(A\boldsymbol{x}=\boldsymbol{b}\)より、\(\boldsymbol{x}=A^{-1}\boldsymbol{b}\)となり\(\boldsymbol{x}\)が求められる。）
ただし、そもそも\(A^{-1}\)が存在しなければ、当然ですが\(A^{-1}\)を掛けることはできません。
ですので、係数行列\(A\)の行列式を計算することで、\(|A| \neq 0\)ならその方程式は解けるし、\(|A| = 0\)ならその方程式は解けない、ということになります。
せんせ最初の例では、係数行列\(A=\begin{pmatrix} 1 & 1 \\ 2 & 2 \end{pmatrix}\)の行列式が\(|A|=1\cdot 2 – 2 \cdot 1\)となるので「解けない」ということになりますね。
まとめ
行列式の求め方と、その意味の説明でした。
正直テクニック的な部分も多いので、なんのために勉強しているかわかりにくい行列…。
ただ、行列は色々なところにポツポツと顔を出すので、できるだけ「なにをしているのか？」というのを理解することをオススメします！
おまけ
たろぅここからは本文に関係ない宣伝です。
このブログはアフィリエイト（宣伝）に参加しているのですが、アフィリエイトの広告って、結構面白いものがあるんですよね。
中には「なにコレ！欲しい！」と思うようなものもあります。結構アフィリエイトの広告って眺めているだけでも面白いです。
私は結構多趣味でパソコン関係からスポーツ、アウトドア、料理…色々やります。そんな私が、有名なASPサイトである「A8.net」と「もしもアフィリエイト」の広告を全て見て「これは面白いな」と思ったものや、実際に利用しているサービスを紹介していきたいと思います！
たろぅちょっと息抜きに見てみてください！
LINEスタンプ
私が作っているLINEスタンプの宣伝です！このブログでも活躍しているクマのLINEスタンプです！
たろぅ気になったらぜひチェックしてみてください！そしてガンガン使ってください！
お友達追加もぜひお願いします！
たろぅ新着スタンプなど、情報発信していきます。他にも「クマ」に関する情報が共有できたら、と思います！
たろぅインスタは結構更新頻度高いです！ちょっとしたマンガも描いてますのでぜひフォローお願いします。
ポイ活
ポイ活は地味にお得なのでコツコツとやってます。買い物したりミニゲームしたりでポイントを稼ぐのが好きな人にはオススメです！
買い物するときはハピタスでポイントを貯めています！有名なポイントサイトなので安心感もありますね。
※１３歳以上で利用可能ですが、未成年者は保護者の同意が必要になります。
たろぅネットショッピングをよくする、という人にオススメ！いろんなネットショッピングがポイントがつつ対象になってます。結構貯まりますよ。
ECナビはアンケートやミニゲームでポイントが稼げるポイントサイトです。こちらも大手サイトなので安心してポイント稼ぎができます。
※ １６歳以上で利用可能ですが、未成年者は保護者の同意が必要になります。
たろぅこちらもまいにちポチポチとゲーム感覚でポイントを稼いでいます。ポイントでおやつ買ったり、ちょっと豪華なお昼ご飯食べたり、プチ贅沢が楽しめるのでポイ活はオススメですね。
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
