PR
三角比の定義について深堀りする【単位円を使った定義まで丁寧に解説】

三角比…高校数学でも「なんであんなの習うの?」となりがちな分野です。
 たろぅ
たろぅ\( \sin{} \)、\( \cos{}\)、\( \tan{}\)がなんぼのもんじゃい!
まぁ、実生活でも役には立っているんですが、専門的な感じが強く、なかなかその恩恵を認識されない三角比…。



そもそもなんであんな定義なわけ?
ということで、この記事では三角比の直角三角形を使った定義から、単位円を使った定義まで解説していきます。
三角比の定義



んー…どうしたもんかなぁ…。



あら?どうかしたの?



いやぁ…この間、ゴルフに行ってさ、上りの距離を見誤っちゃってミスショット連発したんだよねぇ…。高低差を機械で測るのは(公式の)ルールで禁止されてるし…。高低差をサッと計算する方法はないかな?



…あんた、ゴルフが趣味なの?



え?なにか問題でも?
それより高低差を計算する方法を教えておくれよぅ。
三平方の定理なんかは水平距離が必要だから難しいし…。



ま、そんなときは三角比ね。水平方向を基準にした角度なら測れるでしょ?角度と三角比を使えば高低差は計算できるわよ。



え?あの\( \sin{} \)、\( \cos{}\)とか?
ということで三角比です。
この記事では三角比の定義について深堀りしていきますが、たろうくんのように「高低差を知りたい」とかいうシチュエーションでは、三角比の定義を使って簡単に高低差を求めることができます。
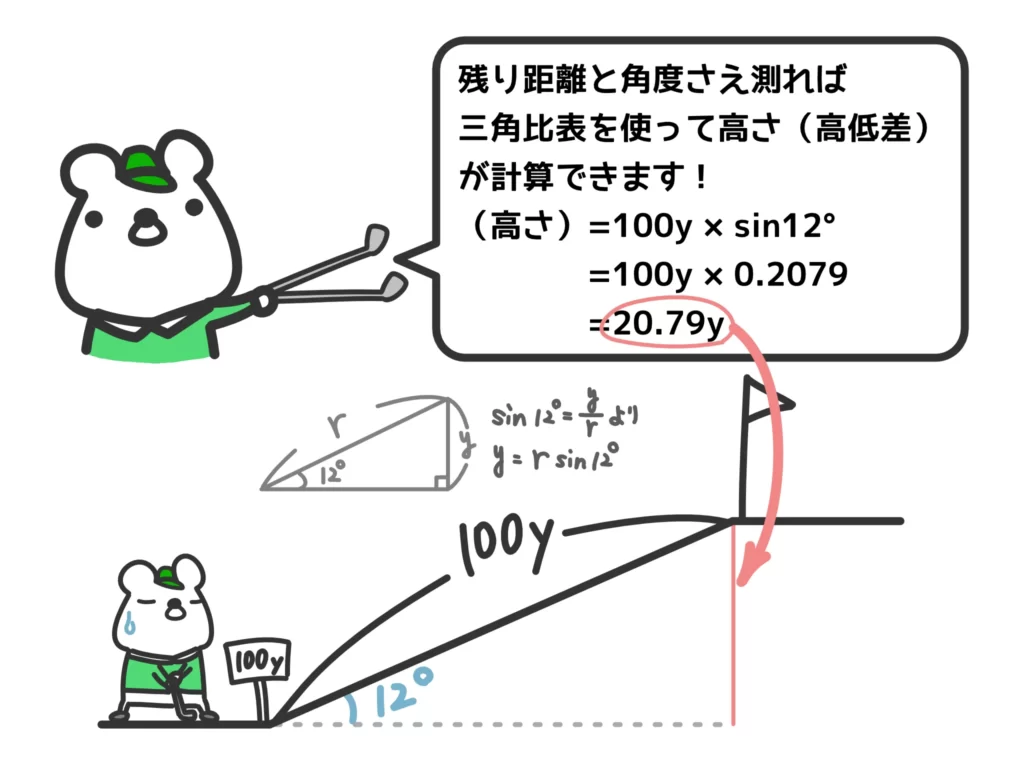

※ ちなみに\(\sin{12°}=0.2079\)は三角比表、という表を使って調べることができます。
三角比の定義
直角三角形の斜辺の長さを\(r\)、高さを\(y\)、底辺の長さを\(x\)とし、斜辺と底辺の成す角を\(\theta\)とすると、
\(\displaystyle \sin{\theta} = \frac{y}{r}\)
\(\displaystyle \cos{\theta} = \frac{x}{r}\)
\(\displaystyle \tan{\theta} = \frac{y}{x}\)
と定義される。
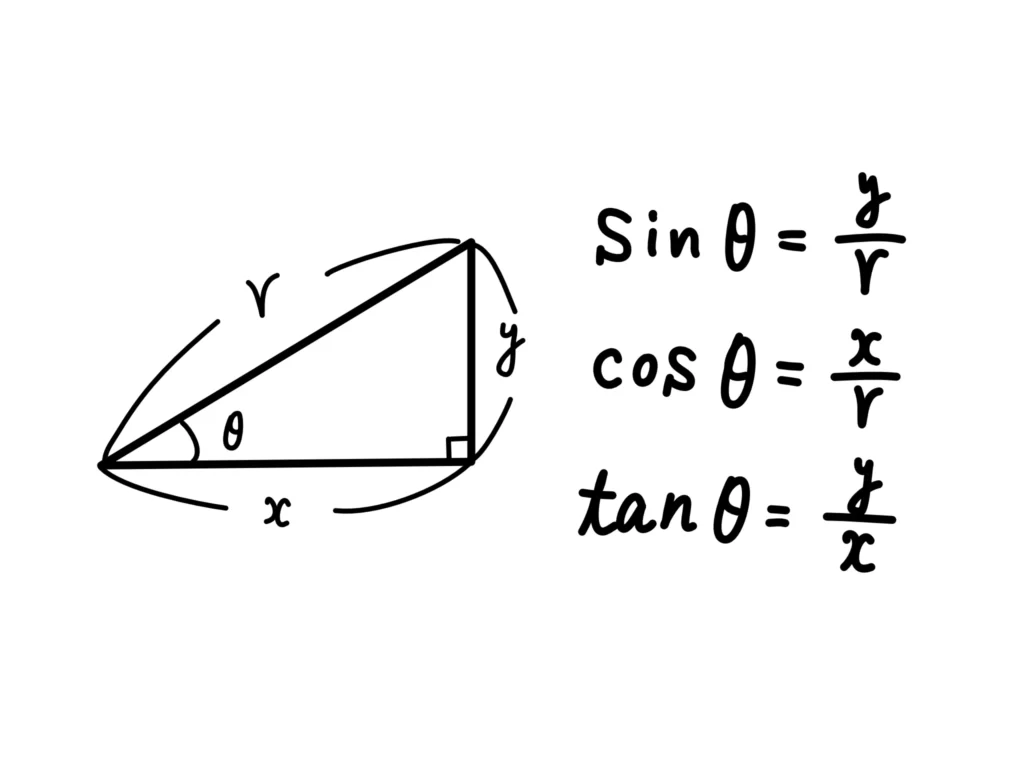
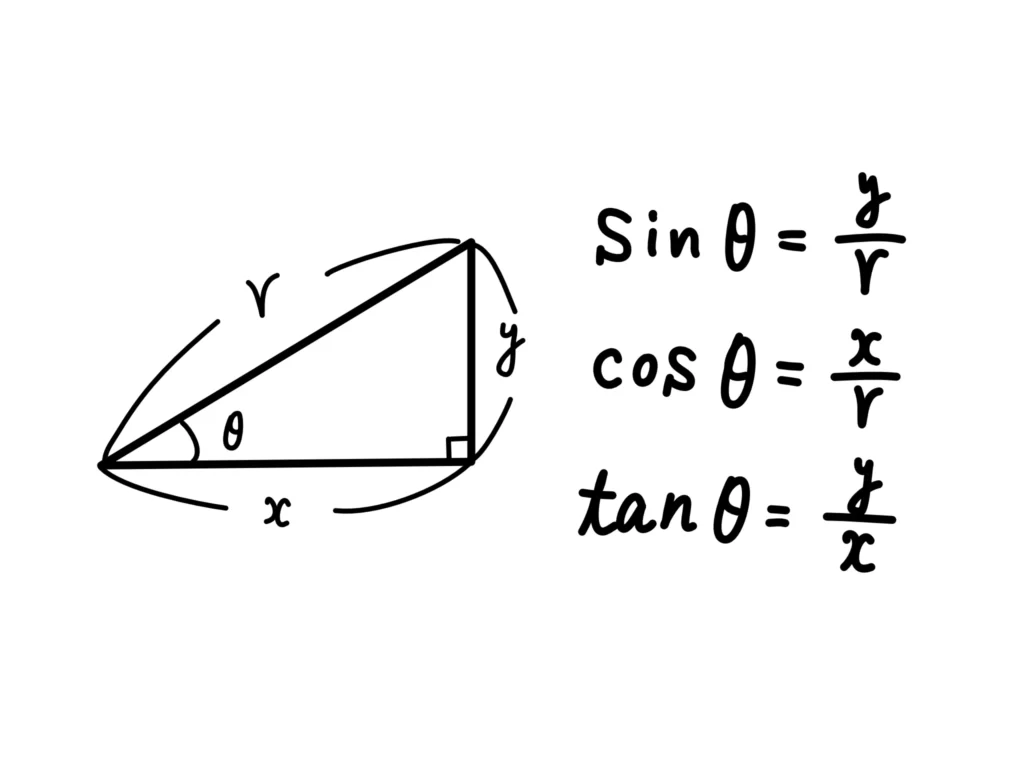
たろうくんの例にもあるように、定義を変形した
- \(y=r\sin{\theta}\)(斜辺と角度で高さがわかる)
- \(x=r\cos{\theta}\)(斜辺と角度で底辺がわかる)
- \(y=x\tan{\theta}\)(底辺と角度で高さがわかる)
はよく使うので押さえておいてください。
直角三角形を使った定義の弱点
ただ、直角三角形を使った定義にはいくつか弱点があります。
- 角度が\( 0° < \theta < 90°\)でしか定義できない。
- 直角三角形の斜辺\(r\)はどんな値でもいいので、定義の方法に統一性がないように見える。
①はわかりやすい弱点ですね。角度は90°を超えるものもあるし、数学IIで角度の拡張を習うと「負の角度」なんかもでてきます。
もう少し汎用性の高い定義方法を考えないといけません。
また、三角比の定義をしたときに、



あれ?直角三角形ってどんな大きさでもいいの?大きいのもあれば小さいのもあるけど…。そんなんで「定義」なんか言っちゃっていいわけ?
と思った人もいるかもしれません。
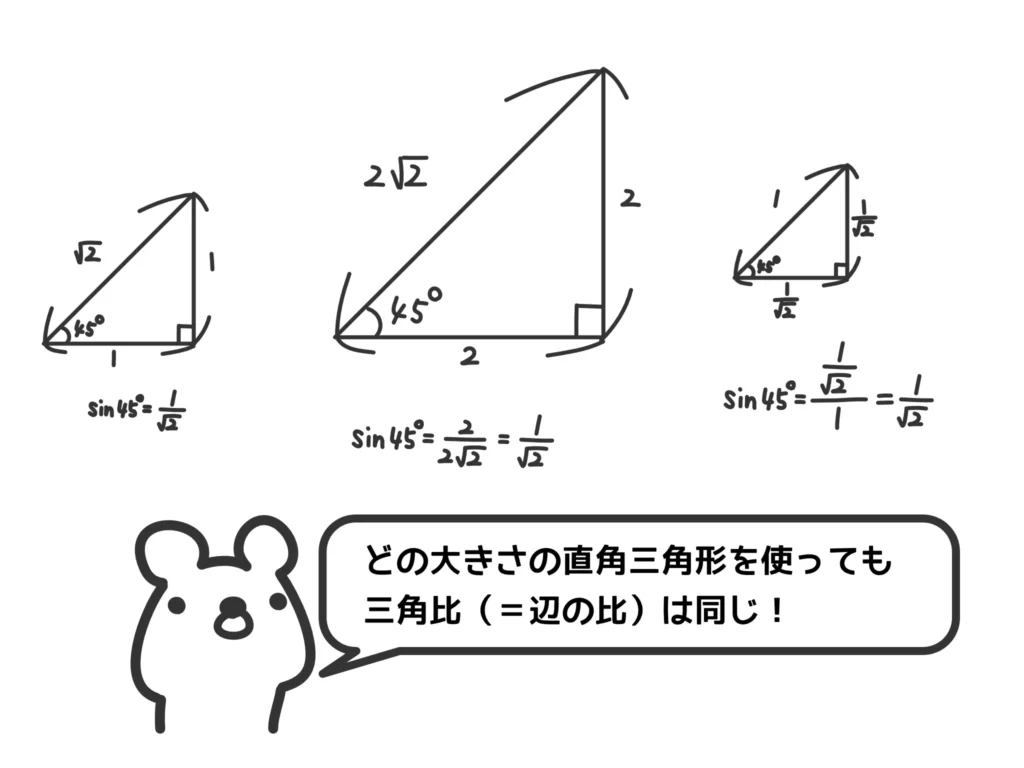
ですが、三角比の定義は「どんな大きさの直角三角形を使ってもOK」なんです。
なぜならば、\(\displaystyle \sin{\theta} = \frac{y}{r}\)、\(\displaystyle \cos{\theta} = \frac{x}{r}\)、\(\displaystyle \tan{\theta} = \frac{x}{y}\)は辺の比だからです。
こちらの記事でも説明しましたが、分数は本質的に比を表しています。


「辺の比」ですから、いわゆる相似な直角三角形であれば、どんな大きさでも辺の比は等しい、ということになります。

そして、「相似な直角三角形である」というのは「直角以外の一つの角度」によって決まるので、辺の比である三角比は角度のみによって決まる値だ、ということもわかります。
しかし、「どんなサイズの直角三角形でも辺の比は同じだから、どれ使ってもOKだよ」と言われると、逆に統一性がなくなって困りますよね。
なにか、統一性のある基準がほしいものです。



ということで、これらの問題を一気に解消する定義方法が「単位円を使った三角比の定義」です。
単位円を使った三角比の定義
ということで、まずは「直角三角形のサイズが統一されていない問題」を片付けましょう。
これは簡単で、斜辺の長さを\(r=1\)に統一すればOKです。

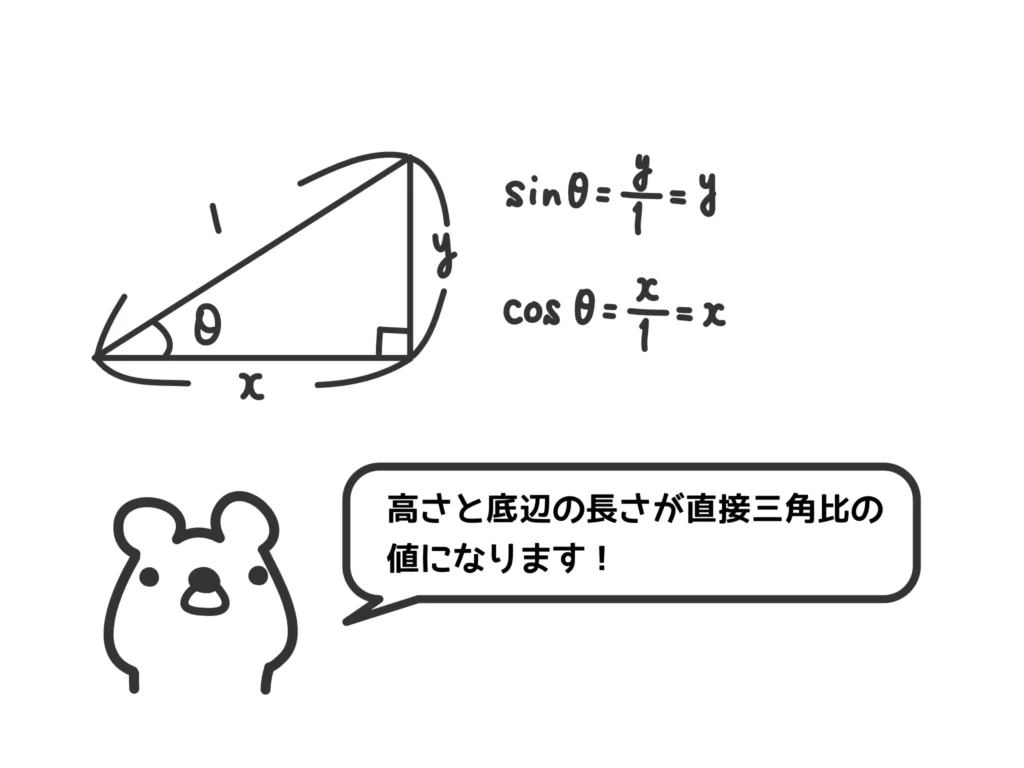
なぜ斜辺の長さを\(r=1\)に統一するかというと、こうすれば、
\(\displaystyle \sin{\theta} = \frac{y}{r} = \frac{y}{1} =y\)
\(\displaystyle \cos{\theta} = \frac{x}{r} = \frac{x}{1} =x\)
となるので、直角三角形の「高さ」=\( \sin{\theta} \)、「底辺の長さ」=\( \cos{\theta} \)となります。「高さ」と「底辺の長さ」がそのまま\( \sin{\theta} \)、\( \cos{\theta} \)になるので都合がいいんですね。




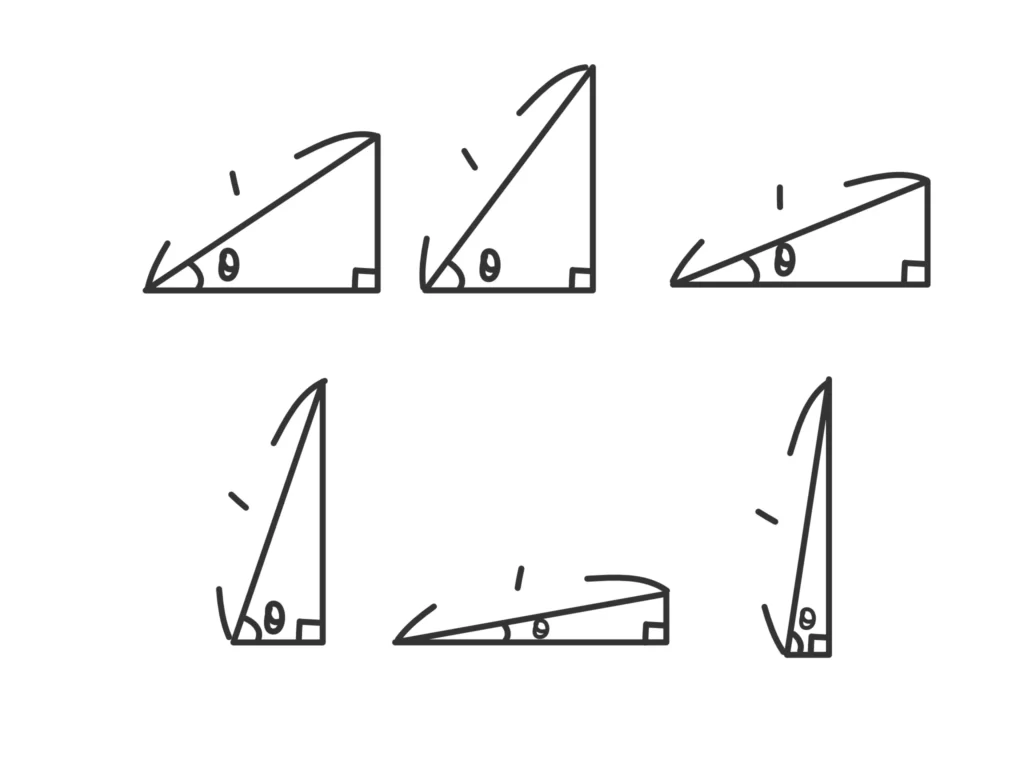
では、このまま\(r=1\)の直角三角形を重ねてみましょう。
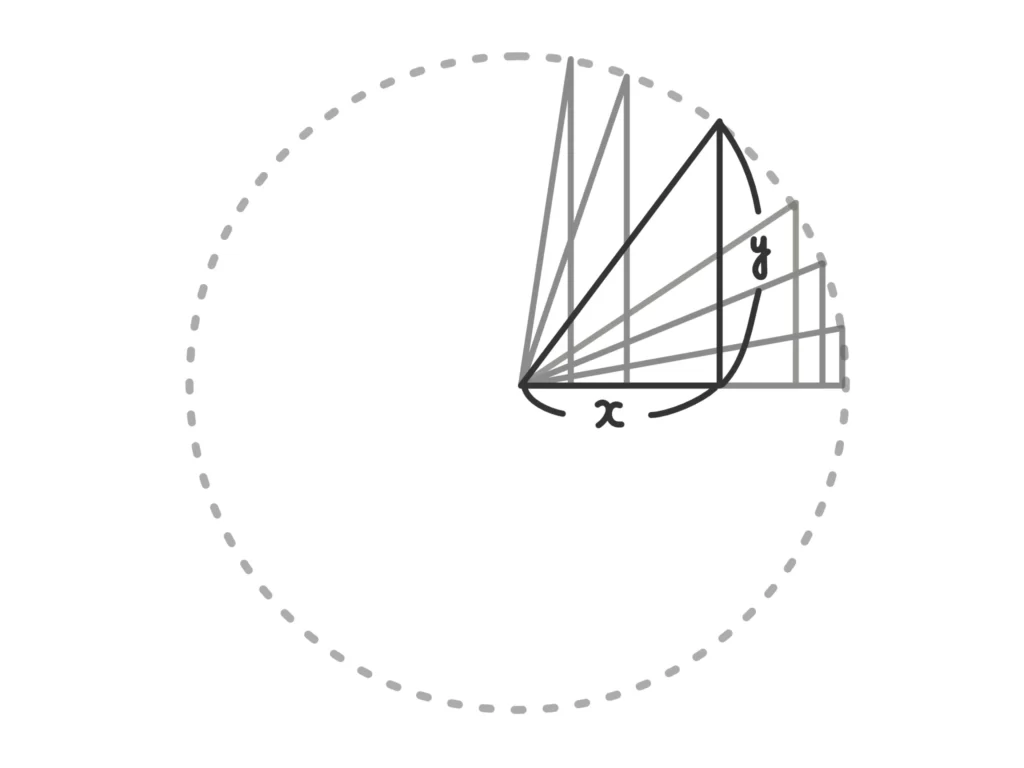

このとき、右上の頂点は半径1の円を描きます。斜辺の長さは\(r=1\)で固定されているので、ちょうど半径になりますよね。
この発想を使って、中心が原点、半径が1の円を考えると、この円上の点の\(y\)座標が\( \sin{\theta} \)、\(x\)座標が\( \cos{\theta} \)になります。
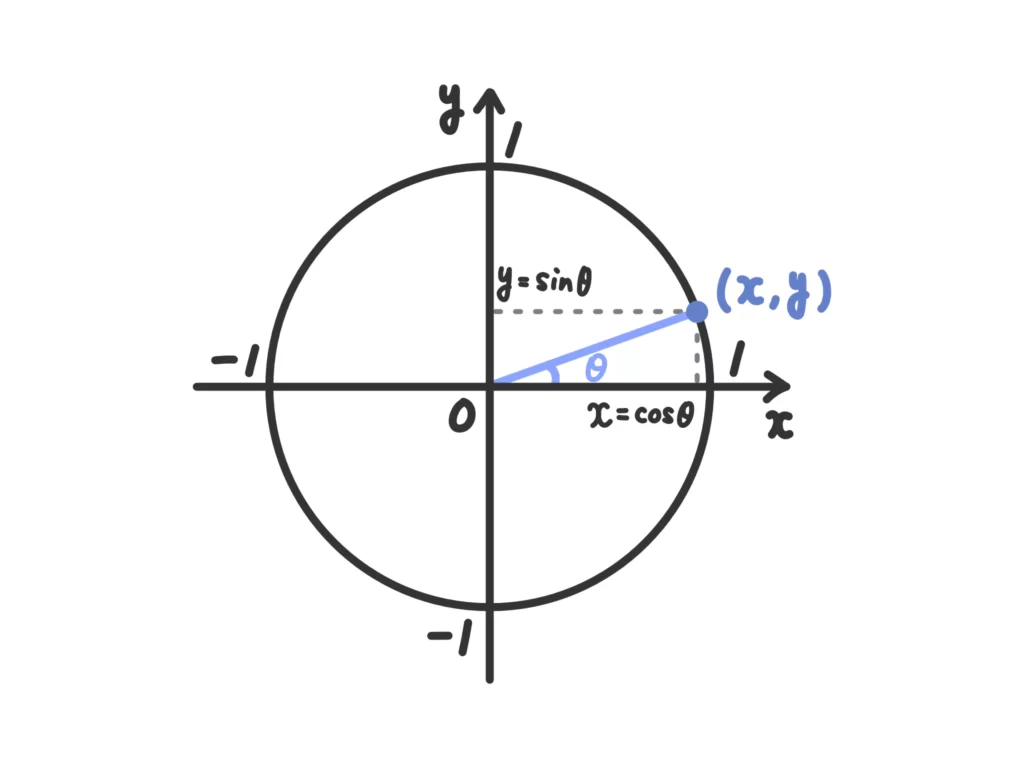

この中心が原点、半径が1の円を単位円といいます。この単位円を使って三角比を定義することができます。
単位円を使った三角比の定義
単位円上の点P\( (x, y) \)と原点を結んだ線分OPが\(x\)軸正の方向と成す角を\(\theta\)とすると、
\( \sin{\theta} = y\)
\( \cos{\theta} = x\)
\(\displaystyle \tan{\theta} = \frac{y}{x}\)


単位円を使うとなにが嬉しいのか?



単位円を使って三角比(関数)の定義をすると、本質的な問題が一気に解決できます。
三角比の角を拡張できる
一番の利点ですね。今まで\( 0° < \theta < 90°\)でしか定義できなかった三角比(関数)の値をどんな角度でも定義できるようになります。



なぜなら、もはや「三角比(関数)の値」=「点の座標」だからです。
唯一定義できないのは90°や270°など、OPが垂直になるときの\(\tan{}\)ですね。これは定義できませんが、その他の\(\sin{0°}=1\)や\(\cos{90°}=0\)なども、単位円上の座標から定義することができます。
また、「点の座標」なので\(\sin\)の値や\(\cos\)の値が(\(\tan\)も)負になることもありますが、これがまた秀逸な性質なんですよね…。余弦定理なんかは\(\cos\)の値が負になることで逆に上手く辺の長さを求めることができます。
三角比や公式を図的に理解できる
個人的には結構重要な利点だと思います。
例えば\(\sin{(90°-\theta)}=\cos{\theta}\)となりますが、この性質は単位円を使えばすぐに理解することができます。


このタイプの公式は後で山程出てくるんですよ…。その全てを正確に覚えて使う、というのはなかなか難しいです。
こういうときに「単位円を使えば導き出せる」というのを覚えていれば公式自体を覚えていなくても全く問題なく対処できます。
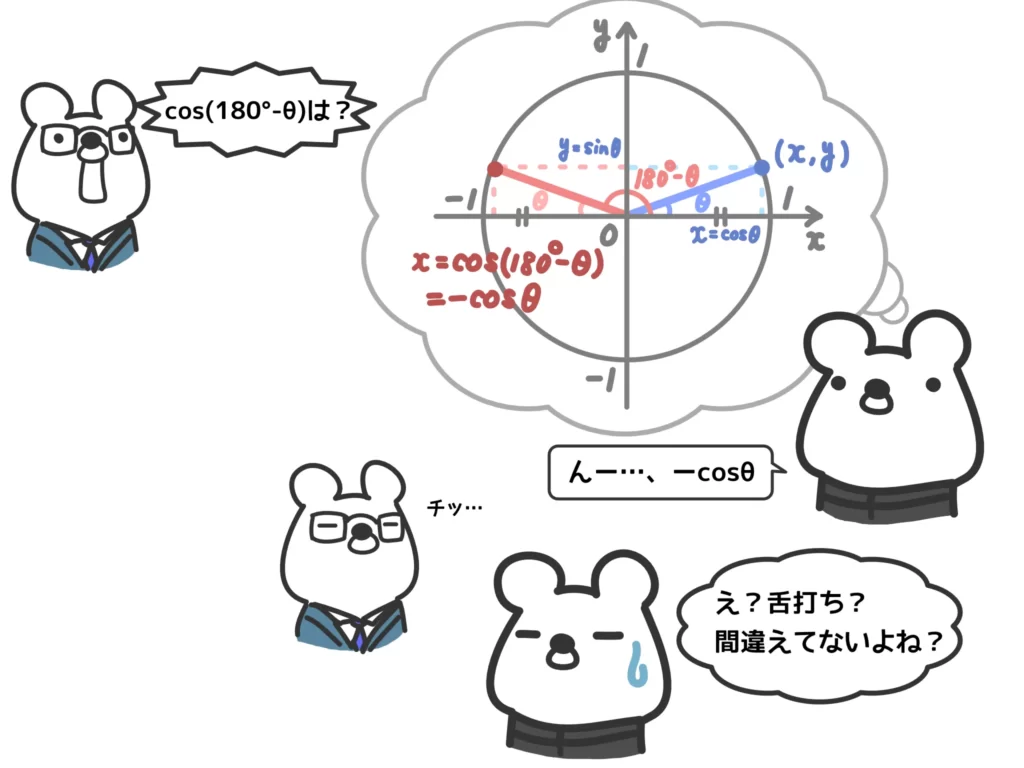




えー…私もこのタイプの公式は一切覚えていません。でも、頭の中に単位円を思い浮かべて導くことができます。
他に覚えるべきことは沢山あります。省エネでいきまよう、省エネで。
数学IIで習う弧度法についても、単位円を使った方が値がわかりやすいです。



例えば、\(\displaystyle \sin{\frac{\pi}{6}}=\sin{30°}=\frac{1}{2}\)とすると、弧度法→度数法に戻すのに無駄なワンステップが必要になります。
単位円を使って図的に値を求めた方がいいですね。
三角比の定義まとめ
三角比の定義についてでした。



三角比の定義はわかったんだけど、なんでこんなのを考えるのかイマイチわかんない…。
という人は、ぜひこちらの記事も読んでみてください。