対数の定義【対数とは？わかりにくいその正体をわかりやすく説明！】

指数関数を習った後に習う対数…。

この対数、

となりがちです。

この記事では、対数の定義と「対数とはなにか？」「対数はどんなときに使えるのか？」について説明していきます。

対数とは？

ということで、対数です。

例えば、上の問題を考えてみます。話を簡単にするため、紙の厚さ0.1mm、月の距離約３８万kmとしましょう。

この紙を半分に折ると厚さは倍になるので、\(0.1 \times 2\)mmとなります。さらに折ると厚さは倍になるので、\(0.1 \times 2 \times 2 \)mm。この調子で紙を\(n\)回折ると、\(0.1 \times 2 \times 2 \cdots \times 2 = 0.1 \cdot 2^n\)mmになります。

これが月までの距離約３８万kmに届くとすると、

\( 0.1 \cdot 2^n\)mm \(> 380000\)km\(=380000000\)m\(=380000000000\)mm
\( 0.1 \cdot 2^n > 380000000000\)

となればOKです。\(0.1\)をはらって、

\( 2^n > 3800000000000\)

この\(n\)を求めればいいのですが…まず手で計算するのはムリですよね？

数学の問題ならともかく、指数の計算というのは現実世界の問題に近づくほど計算不可能なくらい大きくなってきます。

あとで説明をしますが、このようなときに指数部分\(n\)を対数で表すと計算することができます。

もしくは、次のような問題はどうでしょう？

となりますよね？整数の\(x\)で\(2^x = 15\)を満たすものはありません。

ですが、指数関数のグラフを考えると、確かに\(2^x = 15\)を満たす\(x\)は存在しそうです。

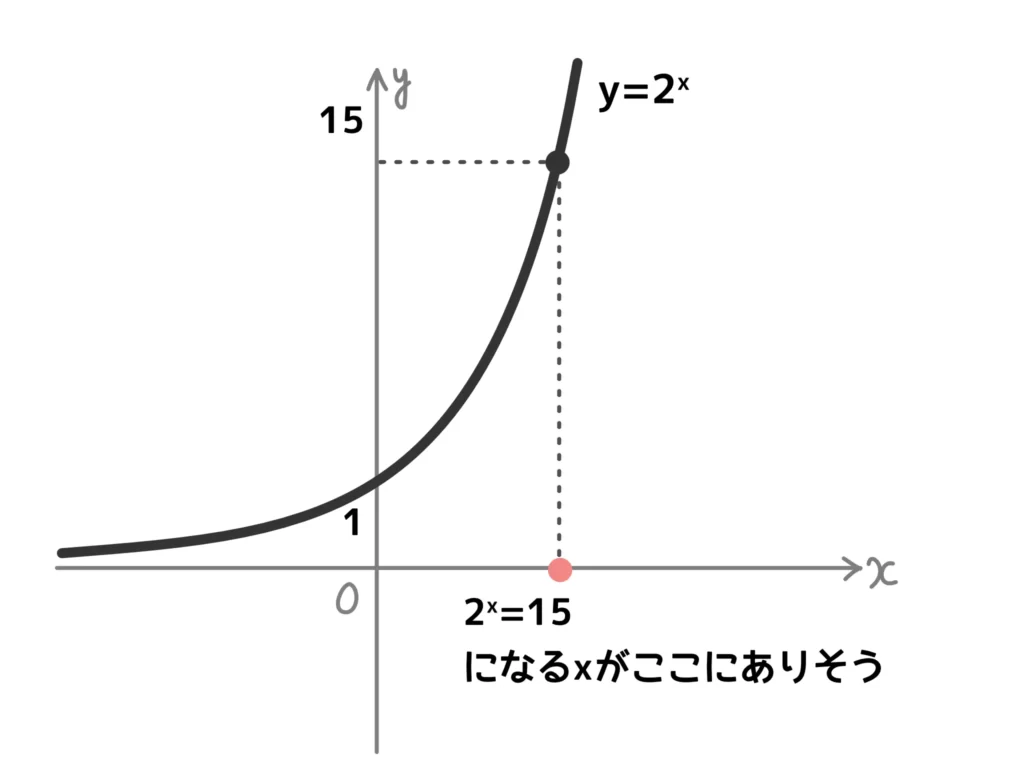
ですが、残念ながらこの\(x\)を表す方法を知りません。

ということで、このような\(x\)を表す新たな方法を「対数」として定義します。

この２つの例で分かる通り、本質的に対数は指数関数の指数部分、という側面があります。…忘れられがちですが。

対数の定義

対数の定義は次のように定められます。

例．\(2^x = 15\)を対数の定義にしたがって変形すると\(x = \log_{2}15\)。

変形のコツは、

• 対数は指数関数の指数部分だ。
• 対数の「底」も指数の「底」同じものだ。

という点を押さえておくことですね。

対数が指数関数の指数部分だ、というのは先程説明したとおりです。

また、\(log_{a}M\)の\(a\)のことを底といいますが、指数の\(a^p\)の\(a\)ことも底といいます。教科書には書いているんですが、対数の方の「\(log_{a}M\)の\(a\)を底という」ことが多すぎて\(a^p\)の\(a\)も底というのを忘れがちです。

対数の定義を見てくれればわかりますが、これらの底はどちらも同じものです。

なので、対数の定義を使って変形する場合は、\(a^p = M\)のとき、

• 対数は指数部分を表すので「\(p=\)」の形だな。
• 対数の底と指数の底は同じだから、「\(\log{a}□\)」の形だな。

→だから\(p = \log{a}M\)だな。と、すんなり変形できます。

対数の定義の練習問題

対数の定義まとめ

対数の定義についてでした。

対数は指数関数の指数部分を上手く表すための表現方法、というのは押さえておきましょう。