PR
一致推定量・不偏推定量とは【平均や分散、不偏分散の一致性・普遍性は?】

平均や分散などを調べるときに、すべてのデータを調査するのが難しい場合があります。
そこで、統計的な手段として、全体(母集団)の中からサンプル(標本)を抽出して調べることで、全体の特徴を推測します。
ですが、ここで疑問に思うのは、
 たろぅ
たろぅ標本の特徴を調べるのはいいけど、全体の特徴とズレがあるんじゃないの?
という点です。
この記事では、統計的な推測をする際の、標本の推定量の「一致性」「不偏性」と不偏分散について説明していきます。
推定量の一致性・不偏性とは?
推定量(標本平均や標本分散)は母集団の性質を推定するための値ですが、当然ですが母集団の性質を正確に推定できる方がありがたいです。
こちらの記事で「大数の法則」について説明をしましたが、標本のサンプルサイズが大きくなればなるほど母集団の性質を正確に推定することができます。





サンプルの推定量と、次の一致性と不偏性は押さえておきましょう。
一致性
例えば、サインプルサイズが大きくなれば標本平均は母平均に近づいていきます。
これを一致性と言います。





こちらは感覚的にわかりやすい性質ですね。
不偏性
一致性は「サンプルサイズが大きくなれば、値そのものが推定したい値(母数)に近づく」という性質です。
一方、不偏性というのは期待値の話です。
例えば、サンプルサイズが小さいときに推定量が推定したい真の値とズレる可能性が高いと信用のある値とは言えません。
サンプルサイズが小さくても大きくても、推定量が推定したい真の値とズレがない値の方が信用できます。
例えば、標本平均の期待値はサンプルサイズが大きくても小さくても同じです。
サンプルサイズが大きい方が標本平均の「値」は母平均に近づきますが、標本平均のとり得る「可能性」はサンプルサイズによりません。
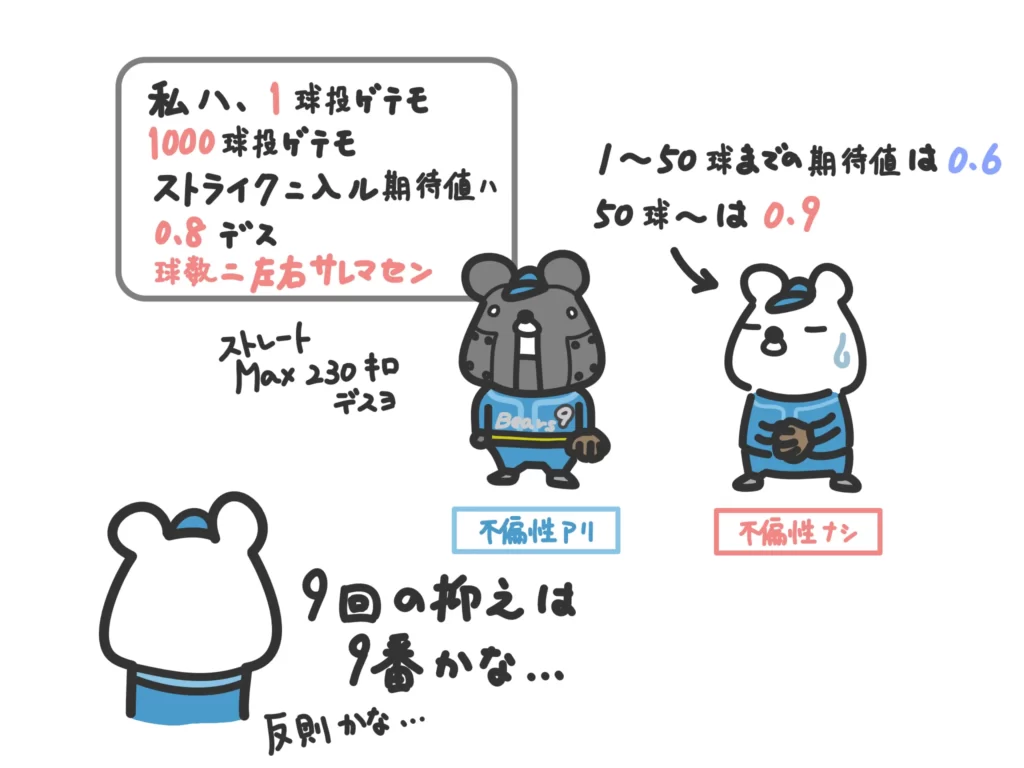

サンプルサイズが小さくても大きくても、標本平均がとる値の「可能性」は母平均の値と一致します。



標本平均を取ったときに母平均と一致する可能性(期待値)は、サンプルサイズの大きさによらない、ということですね。サンプルサイズが大きくても小さくてもその可能性に偏りがない(不偏性がある)ということですね。
標本平均や標本分散は一致推定量?不偏推定量?
代表的な推定量の一致性と不偏性



ふーん…じゃあまぁ、推定量(平均とか分散とか)は一致性とか不偏性とかをもってるんですね。
と思うかもしれませんが、ところがどっこい、ちょっと注意しないといけないポイントがあります!



代表的な推定量の一致性・不偏性について表にまとめておきます。
| 一致性 | 不偏性 | |
|---|---|---|
| 標本平均 | ○ | ○ |
| 標本分散 | ○ | × |
| 不偏分散 | ○ | ○ |
よく見かける推定量は大体一致性・不偏性を持ちますが、代表的な例外として標本分散があります。
標本分散は一致性はもちますが、不偏性はもちません。
後ほど「不偏分散」と一緒に少し詳しく説明しますが、標本分散の期待値は母分散よりも小さくなります。サンプル数が大きくなれば精度は上がりますが、サンプル数が小さいほど母分散よりも小さくなります。



標本分散は、サンプルサイズが小さいと母分散よりも小さい値が出る可能性が高くなる、ということですね。
これでは不偏性をもっている、とは言えませんね。
ということで、統計的な推測の話で分散を使いたければ、不偏分散というものを使います。
不偏分散について
以下の式で定められる値を不偏分散と言います。
不偏分散
不偏分散\(s^2\)はその名の通り、不偏性をもつ分散です。高校教科書レベルでは使いませんが、統計検定などでは母集団の推測をする際によく使います。
\(\displaystyle s^2 = \frac{1}{n-1} \{(x_1 – \bar{x})^2 + \cdots + (x_n – \bar{x})^2 \} \)
ただし、\(\bar{x}\)は標本平均とする。



標本分散のときは\(n\)で割りますが、そこを単純に「\(n-1\)で割る」に変えただけですね。
(証明)
まずは普通の標本分散が不偏性をもたないことを示していきます。
もう一度押さえておきますが、「推定量の期待値が真の値と一致する」ときにその推定量は不偏性をもつ、といいます。
つまり、「標本分散の期待値や不偏分散の期待値が母分散と一致するか?」を確認すればよい、ということになります。



ということで、まずは\(E[(標本分散)]\)を計算していきます。
面倒なので、標本分散を\(\displaystyle \frac{1}{n}\sum{(x_i-\bar{x})^2}\)と書きます。また、母平均を\(\mu\)、母分散を\(\sigma^2\)(←一致してほしい値)とします。
\(\displaystyle E \left[ \frac{1}{n}\sum{(x_i-\bar{x})^2} \right] = E \left[ \frac{1}{n} \sum{ \{(x_i-\mu)-(\bar{x}-\mu) \}^2 } \right]\)
\(\displaystyle \quad = E \left[ \frac{1}{n} \sum{ \{(x_i-\mu)^2-2(x_i-\mu)(\bar{x}-\mu)+(\bar{x}-\mu)^2 \} } \right] \)
\(\displaystyle \quad = E \left[ \frac{1}{n}\sum{ (x_i-\mu)^2 } \right] -2(\bar{x}-\mu) E \left[ \frac{1}{n}\sum{(x_i-\mu)} \right] + E\left[ \frac{1}{n}\sum{(\bar{x}-\mu)^2} \right] \)
\(\displaystyle \quad = E \left[ \frac{1}{n}\sum{ (x_i-\mu)^2 } \right] -2(\bar{x}-\mu)E \left[ \frac{1}{n}(x_i+\cdots + x_n) – \frac{1}{n} \cdot n\mu \right] + E\left[ \frac{1}{n} \cdot n ( \bar{x}-\mu )^2 \right] \)
\(\displaystyle \quad = E \left[ \frac{1}{n}\sum{ (x_i-\mu)^2 } \right] -2(\bar{x}-\mu)E \left[ \bar{x} -\mu \right] + E\left[ (\bar{x}-\mu)^2 \right] \)
\(\displaystyle \quad = E \left[ \frac{1}{n}\sum{ (x_i-\mu)^2 } \right] – E\left[ (\bar{x}-\mu)^2 \right] \)
(↑第2、3項の\(-2(\bar{x}-\mu)E \left[ \bar{x} -\mu \right]+ E\left[ (\bar{x}-\mu)^2 \right]=-2E \left[ ( \bar{x} -\mu )^2 \right]+ E\left[ (\bar{x}-\mu)^2 \right]=- E\left[ (\bar{x}-\mu)^2 \right]\)だから)
ここで、一つずつ見ていくと、第1項は
\(\displaystyle E \left[ \sum{ \frac{1}{n} (x_i-\mu)^2 } \right] = \frac{1}{n} \left\{ E [ (x_1-\mu)^2 ] + \cdots + E [ (x_n-\mu)^2 ] \right\} \)…①
と分けることができますが、
\(\displaystyle E [ (x_1-\mu)^2 ] \cdots\)はサンプルサイズが1の分散なので(偏差の二乗の期待値=分散)、母分散と一致します。
\(\displaystyle E [ (x_1-\mu)^2 ] = V[x_1] = \sigma^2 \cdots\)
よって、
\(\displaystyle (①)= \frac{1}{n} (\sigma^2 + \cdots + \sigma^2 ) = \frac{1}{n} \cdot n\sigma^2 = \sigma^2 \)
第2項は、
\( E\left[ (\bar{x}-\mu)^2 \right] = V \left[ \bar{x} \right] \)
\(\displaystyle \quad = V\left[ \frac{x_1 + \cdots + x_n}{n} \right] \)
\(\displaystyle \quad = \frac{1}{n^2} (V[x_1] + \cdots + V[x_n]) \)(←分散の変数変換参照)
\(\displaystyle \quad = \frac{1}{n^2} \cdot n \sigma^2 = \frac{1}{n}\sigma^2\)
以上より、
\(\displaystyle E \left[ \frac{1}{n}\sum{(x_i-\bar{x})^2} \right] = \sigma^2 – \frac{1}{n}\sigma^2 = \frac{n-1}{n}\sigma^2\)



ということで、単純な標本分散の期待値は\(\displaystyle \frac{n-1}{n}\sigma^2\)になっちゃうので、母分散とズレるんですね。\(n\)が大きければ精度が上がりますが、不偏性(\(n\)が大きくても小さくても期待値が真の値と一致する)はもっていません。
ということで、期待値が\(\sigma^2\)と一致するためには、\(\displaystyle \frac{n}{n-1}\)を掛けてやればいい、ということになります。
\(\displaystyle \frac{n}{n-1} E \left[ \frac{1}{n}\sum{(x_i-\bar{x})^2} \right] = \frac{n}{n-1} \cdot \frac{n-1}{n}\sigma^2 = \sigma^2 \)
ここで、出だしの\(\displaystyle \frac{n}{n-1} E \left[ \frac{1}{n}\sum{(x_i-\bar{x})^2} \right]\)は期待値の変数変換の性質を使うと、
\(\displaystyle \frac{n}{n-1} E \left[ \frac{1}{n}\sum{(x_i-\bar{x})^2} \right] = E \left[ \frac{n}{n-1} \cdot \frac{1}{n}\sum{(x_i-\bar{x})^2} \right]\)
\(\displaystyle \quad = E \left[ \frac{1}{n-1}\sum{(x_i-\bar{x})^2} \right]\)
よって、「\(\displaystyle \frac{1}{n-1}\sum{(x_i-\bar{x})^2}\)の期待値が\(\sigma^2\)と一致する」という不偏性を持つので、これを不偏分散としましょう、というお話です。



なので、正確には\(n-1\)で割るんじゃなくて、「標本分散を\(\displaystyle \frac{n}{n-1}\)倍する」の方が正しいですね。
まとめ
推定量の一致性と不偏性についてでした。
統計的な推測に関する基本的な性質ですが、一致性と不偏性のイメージと、今回説明した不偏分散はよく使うので押さえておいてください。