条件付き確率とは？AかつBと違う？公式の意味は？わかりやすく説明！

2022年9月20日2024年10月10日

条件付き確率…結構高校でも、つまずく生徒が多いですね。

「条件付き確率って…まぁ計算方法はわかるけど、なんでそんなことするのかいまいちわかんない」という人もいるのではないでしょうか？

ですが、この条件付き確率、実用面でかなり有用な確率になります。

この記事では、条件付き確率の基本とその意味を理解してもらえたら、と思います。

条件付き確率とは？

せんせ

はい、では問題です。

たろぅ

うわー！いや！！帰る！！！

せんせ

帰しません。答えてください。

たろぅ

…なんの問題ですか？

せんせ

確率です。条件付き確率ってなんですか？

たろぅ

あー…確かこの前習ったけど、ちょっとわかんなかったんですよね。「なんですか？」っていうのは、定義を言えばいいんですかね？

せんせ

まぁ、それでもいいですけど、どんな意味があるんですかね？

たろぅ

…帰る！！

条件付き確率…実は２０１２年の教育課程から「数学A 確率」で学ぶようになった（それまでは「数学C」にあったのだが、授業で習った、という人は多分ほとんどいない。そのころ数学Cは「行列」「２次曲線」「確率分布」「統計」があったのだが、「確率分布」「統計」を習った人はほとんどいないと思う。）ので、もしかしたら知らない人もいると思います。

条件付き確率、とは、

事象Aが起きた下で事象Bが起きる確率のことで、\(\displaystyle P_A(B)\)と書き、

\(\displaystyle P_A(B) =\frac{n(A \cap B)}{n(A)}=\frac{P(A \cap B)}{P(A)}\)

で計算することができます。

※１ \(n(A)\)は「事象Aの場合の数」の意味。

※２ \(\displaystyle \frac{n(A \cap B)}{n(A)}\)の分母・分子を全事象の個数\(n(U)\)で割れば、\(\displaystyle \frac{\frac{n(A \cap B)}{n(U)}}{\frac{n(A)}{n(U)}}=\frac{P(A \cap B)}{P(A)}\)となります。

また、表記の話になりますが「事象Aが起きた下で事象Bが起きる確率」を

\(\displaystyle P_A(B)\)とも書きますし、

\(\displaystyle P(B|A)\)とも書くことがあります。後者の方は、BとかAに色々な情報を追加したいときによく使います。

たろぅ

うーん…。正直意味がわかんない、というか、普通の確率と何が違うのかよくわかんないんですけど。

せんせ

そうですね、条件付き確率は、「計算方法はわかるんだけど、よく意味がわかんない」という人が多いです。せっかくですので、条件付き確率の意味を考えていきましょう。

ちなみに、上記のように「個数」で計算してもいいですし、「確率」で計算してもいいです。よく「確率で計算しないといけない」と思っている人もいますが、問題の状況によります。

「個数」がわかる状況でわざわざ確率を計算する必要はありませんし、「確率」しか与えられない状況ではわざわざ個数を考える必要はありません。

数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！

普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！

条件付き確率ってなんだ？「AかつB」と違うの？

たろぅ

せんせい、「AかつBが起きる確率」と「Aが起きた上でBが起きる確率」って違うんですか？

せんせ

違います。

たろぅ

その辺がわかんないんですけど…。

せんせ

そこがまさに「条件付き確率」の話ですね。

結論から言うと、「AかつBが起きる確率」と「Aが起きた上でBが起きる確率」は分母が違います。

普通、確率といえば分母に来る数は「全事象の場合の数」ですね。つまり\(n(U)\)です。

単純に「AかつBが起きる確率」といわれたら、\(\displaystyle \frac{n(A \cap B)}{n(U)}\)で計算します。

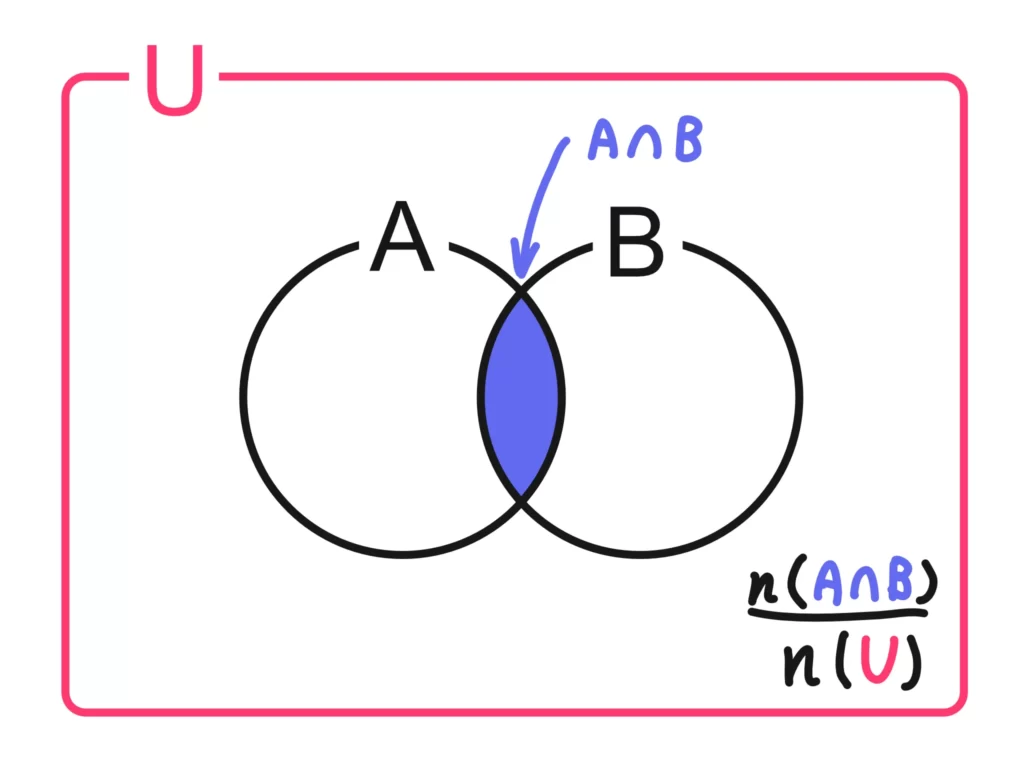
一方、「Aが起きた上でBが起きる確率」といわれたら、条件付き確率になります。「Aが起きた上で」なので、分母が「事象Aの場合の数」になります。つまり\(n(A)\)です。

\(\displaystyle \frac{n(A \cap B)}{n(A)}\)で計算します。

たろぅ

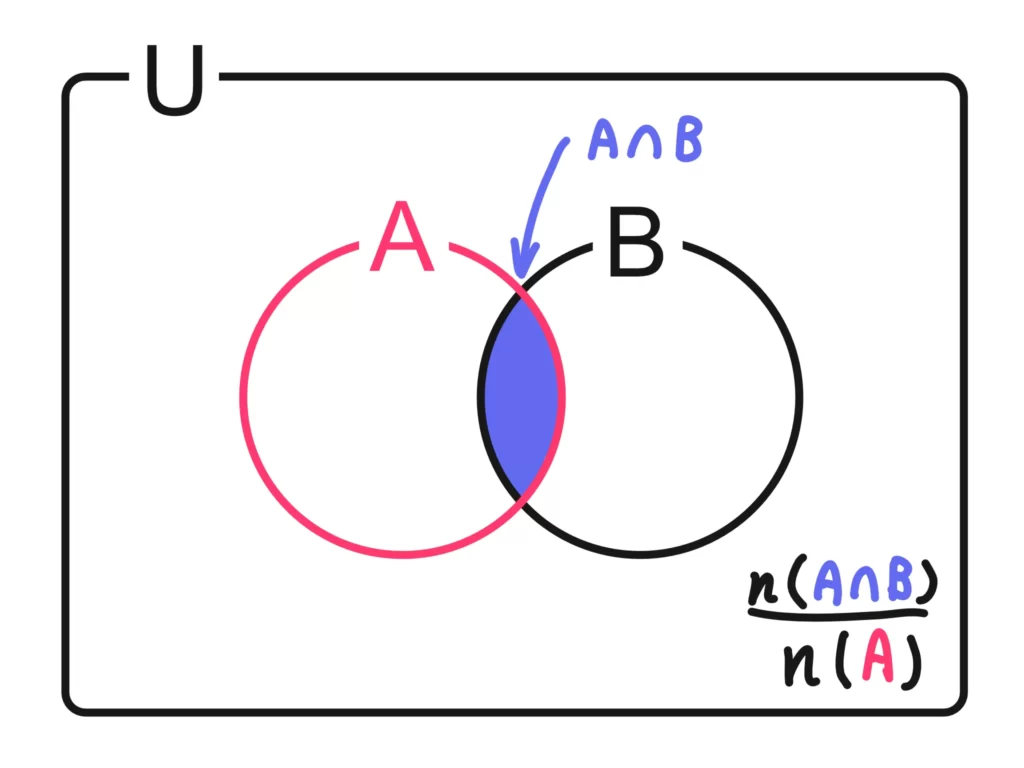
なるほど…普通「確率」といわれたら分母が「全ての場合の数」だけど、「条件付き確率」は分母が「その条件の場合の数」なんですね。

せんせ

その通りです！

たろぅ

でも、やっぱりなんでわざわざそんなことするのかわかんないんですけど…。

例１．交通事故に遭う確率

例えば、「交通事故は年間約３０万件。免許保持者が約８０００万人です。ということは、年間で交通事故に遭う割合は３０万÷８０００万＝０．００３７５（０．３７５％。２６６年に一回事故る。多分一生に一回起きれば「不運だったな」くらい。）です。」

さて、これは計算上は正しいです。

ですが、実際「あなたが運転していたときに交通事故に遭う確率」として適切でしょうか？

たろぅ

いや、計算でそのくらい、って出てるんだから、そりゃそうでしょ？

じゃあ、この「免許保持者８０００万人」は全員もれなく毎日運転してるんですね？

たろぅ

…ん？

「長期休暇にしか運転しない人」「ペーパードライバー（免許だけ持っていて運転は全然しない人）」とかもいますよね？ちなみにペーパードライバーは約３０％と言われています（←あまり信頼性のある情報ではないです。統計として正確な情報がほとんど見つかりませんでした）。「運転免許保持者８０００万人」の中には全く運転しない人も含まれていますよね？

たろぅ

う…。そうですけど…。

仮に３０％がペーパードライバーだったとしましょう。すると、８０００万人のうち、実際に運転している人は７０％の５６００万人になります。

たろぅ

まぁ…現実問題としてはそうですけど…。

そうなると、「運転していたとして、事故に遭う確率」は、実際に運転しているであろう「５６００万人」を分母にする方がいいのではないでしょうか？

たろぅ

…。

ということで、改めて計算すると、「３０万÷５６００万人＝０．０５（５％。２０年に１回は事故る。一生に２、３回くらいは事故る。）」ということになりませんか？

たろぅ

なるほど。必ずしも全体を分母にするのが適切、とは限らないわけですね？

※ 各数値に関しては、インターネット上の情報をかき集めたもので、必ずしも信頼のおける値ではありません。あくまで「条件付き確率の有用性を説明する」目的であると思っていただければ、と思います。

最近では自動運転という技術も発展していますが、全体における事故率を考えても仕方ないですよね？

なぜなら、「見通しのいい直線」「交差点」「公園のそばを通るとき」「細くて混む道」「広くて走りやすい道」…それぞれの条件で事故に遭う確率は全然違いますよね？

分母を全体にする、というのは実は実生活においてはかなり大雑把なことをしている、と思ってください。

条件付き確率は「条件による分母の絞り込み」なのです。

例２．モンティ・ホール問題

有名な、「直感に反する問題」ですね。

「モンティ・ホール問題」

ある番組のラスト、景品をかけたクイズが行われます。

３つの箱A、B、Cのうち１つには「当たりの景品パジェロ（車）」、残り２つには「ハズレのたわし」が入っています。

３つの箱のうち１つを選んで、中に入っているものがもらえる、という単純なゲームです。

あなたは司会者のホイッスルと同時に、１つの箱を選びました。

実は、司会者はどの箱に当たりの景品が入っているか知っています。そこで、その司会者がいきなり、あなたが選ばなかった２つの箱のうち、ハズレの箱をオープンしちゃいました。これで、残りの箱は「あなたが選んだ箱」と「選ばなかった箱のうちの１つ」の２つになりました。

司会者がこう言います。

「選んだ箱を変えてもいいですよ？」

あなたは観客の「パジェロ！パジェロ！」というコールの中考えます…選んだ箱を変えますか？変えませんか？

たろぅ

ん？別に変えようが、変えまいが一緒なのでは？残ってるのは「当たり」「ハズレ」の１つずつだから確率としては\(\displaystyle \frac{1}{2}\)でしょ？

せんせ

そうですね、それは「条件付き確率の考え方」ですね。そういう意味では正解です。

ちなみに、単純に３つから１つの当たりを選ぶ確率は\(\displaystyle \frac{1}{3}\)、１つハズレをさらされた後でランダムに選び直すなら当たりを選ぶ確率は\(\displaystyle \frac{1}{2}\)、ですね。

「条件による分母の絞り込み」が行われており、当たる確率が上がっていますね。

せんせ

だが、しかぁし！！

たろぅ

おわっ！急に大声出すのやめてください。

せんせ

心持ち一つで確率は変わるのです！

たろぅ

心持ちの問題なのか？

さっきのは「変えるか」「変えないか」をランダムに決めた場合の確率です。

実はこの問題、心持ち、というか少し戦略的にやればさらに確率は上がります！

① 「変えない！」と決めている場合

当然最初の段階で当たりを引いておく必要があります。確率は\(\displaystyle \frac{1}{3}\)です。

② 「変える！」と決めている場合

２通りのアプローチで考えてみます。が、どちらも言い換えのようなものです。

１．もしも最初に当たりを引いていたら…

変えた場合、必ずハズれます、１００％です。ですが、そもそも最初に当たりを引く確率が\(\displaystyle \frac{1}{3}\)なので、そのまま、最終的にハズれる確率は\(\displaystyle \frac{1}{3} \cdot 1 = \frac{1}{3}\)となります。余事象で考えると、最終的に当たる確率は\(\displaystyle 1- \frac{1}{3}=\frac{2}{3}\)です。

２．もしも最初にハズレを引いていたら…

変えた場合、必ず当たります、１００％です。しかも、そもそも最初にハズレを引いておかないといけないので、その確率は\(\displaystyle \frac{2}{3}\)です。確率としては高いですよね。変更すればそのまま当たるので、最終的に当たる確率は\(\displaystyle \frac{2}{3} \cdot 1 = \frac{2}{3}\)となります。

たろぅ

なるほど…「必ず変える」と決めていれば、確率はさらに上がるんですね。要は最初にハズレを引いていれば、変更すれば必ず当たるのか…。

せんせ

そういうことですね。よくある例ですが、これを「当たり１個」「ハズレ９９個」の合計１００個で同じようなことをしたら、更にわかりやすくなりますね。

「当たり１個」「ハズレ９９個」でやってみる。

１つ選ぶ。

司会者はハズレをさらすときに、残りの９９個からハズレ９８個をさらす。（残り１個は当たりかもしれないし、ハズレかもしれない。）

これで残りは「選んだ１個」と「残りの９９個からハズレ９８個を取り除いた１個」ですね。

どっちを選びますか？

こうなると、逆に直感的にわかりやすくなるんじゃないでしょうか？

「選んだ１個」って、一発目に当てないとダメですよね？当然確率は\(\displaystyle \frac{1}{100}\)です。

「残りの９９個からハズレ９８個を取り除いた１個」って、当たりである可能性がめちゃくちゃ高いですよね？一発目で当たりを引いていなければ、その１個は自動的に当たりになるんですから。変えれば当たる確率は\(\displaystyle \frac{99}{100}\)です。だって一発目にハズレを引いてればいいんですから。

たろぅ

なるほど、単純な条件付き確率ではなくて、考えて戦略的にすればもっと確率を上げることができる…という問題ですね。