PR
底の変換公式の証明と底の決め方など…底の変換完全攻略！
「底の変換公式」は数学IIの指数・対数関数の対数を勉強していたら出てきます。
ですが、この「底の変換公式」は対数の底を自由に定めることができるので、どのように底を定めていいか？がわからない人が多いようです。
この記事では底の変換公式の証明と使い方、それともう一歩踏み込んだ、底の変換公式の「本当の意味」を解説していきます。
目次
底の変換公式の証明
せんせ…たろうくん。
たろぅ（ドキッ！！）…なんですか？
せんせさっきの授業…寝てましたね？
たろぅ（ばれてた…）そ、そんなわけないじゃないですか。ちょっと目をつぶって数学のことと今後の人生について考えていただけです。
せんせ罰として、次の授業の「底の変換公式」の証明を解説してください。
たろぅえー…。それは先生の仕事でしょお…。
せんせ私の仕事はあくまで「生徒の成長を手助けする」というものであって、数学を解説するのが仕事ではありません。数学を通して生徒が成長すればよいのです。ですから、この証明をたろうくんが解説することで、たろうくんが成長できればそれでよいのです。
たろぅんー…。もっともなような、だまされているような…。
底の変換公式とは次のようなものです。
底の変換公式
\(c\)を\(c>0\)かつ\(c \neq 1\)とするとき、
\(\displaystyle \log_a b = \frac{\log_c b}{\log_c a}\)
対数の底\(a\)が気に食わなければ、好きな底\(c\)に変換していいよ、というなんとも都合のいい公式です。
たろぅむぅ…これの証明かぁ…。とりあえず教科書見るか…。
（証明）
\( \log_a b = p\)とする。
対数の定義にしたがって、指数の形にすると、
\(a^p = b\)
両辺、底\(c\)の対数をとる。
\(\log_c a^p = \log_c b\)
\(p \log_c a = \log_c b\)
\(\displaystyle p = \frac{\log_c b}{\log_c a}\)
よって、\(\displaystyle \log_a b = \frac{\log_c b}{\log_c a}\)（終）
たろぅふぅ…こんな感じかな。
このブログで活躍してるクマのLINEスタンプもあります！
底の変換公式の底の決め方
結論から言うと、問題を解く際にはどのような底に変換しても問題はありません。ただし、問題によって「解くのに効率がいい底」というものはあります。
せんせ例題を一つ解いてみましょう。
例１．\(\log_3 5 \cdot \log_5 9 \)を計算せよ。
（解答１）
どちらかの底に揃える、というのがセオリーです。
\(\displaystyle \log_3 5 \cdot \log_5 9 = \log_3 5 \cdot \frac{\log_3 9}{\log_3 5}\)（←底3に揃えた）
\(\displaystyle \quad = \log_3 5 \cdot \frac{\log_3 3^2}{\log_3 5}\)
\( \quad = 2\log_3 3=2\)…（答）
（解答２）
底を５に揃えても問題はありません。
\(\displaystyle \log_3 5 \cdot \log_5 9 = \frac{\log_5 5}{\log_5 3} \cdot \log_5 9\)（←底5に揃えた）
\(\displaystyle \quad = \frac{\log_5 5}{\log_5 3} \cdot \log_5 3^2\)
\(\displaystyle \quad = \frac{1}{\log_5 3} \cdot 2\log_5 3=2\)…（答）
（解答３）
全く関係ない底にしても問題はありません。ただし、非効率なのでこういう底の選び方はしません。
\(\displaystyle \log_3 5 \cdot \log_5 9 = \frac{\log_{10} 5}{\log_{10} 3} \cdot \frac{\log_{10} 9}{\log_{10} 5}\)（←問題と全く関係ない、底10に揃えた）
\(\displaystyle \quad = \frac{\log_{10} 5}{\log_{10} 3} \cdot \frac{\log_{10} 3^2}{\log_{10} 5}\)
\(\displaystyle \quad = \frac{\log_{10} 5}{\log_{10} 3} \cdot \frac{2\log_{10} 3}{\log_{10} 5}=2\)…（答）
コツは「なるべく問題に関わりのありそうな数の底を選ぶ」ということです。
今回の問題なら、どちらかの底に揃えるべきでしょう。つまり底3か底5がいいと思います。テクニカルな話になってしまいますが、これがセオリーです。
たろぅまぁ最悪どんな底でも問題は解ける、と知っておけば安心感はありますよね。
せんせもう一つ例を出しましょう。
例２．\(\log_4 18 – \log_8 54 \)を計算せよ。
（解答１）
どちらかの底に揃えるのがセオリーですので、底4に揃えてみます。
\(\displaystyle \log_4 18 – \log_8 54 = \log_4 18 – \frac{\log_4 54}{\log_4 8} \)
\(\displaystyle \quad = \log_4 2 \cdot 3^2 – \frac{\log_4 2 \cdot 3^3}{\log_4 2^3} \)（←真数を素因数分解しておくと…）
\(\displaystyle \quad = \log_4 2 + \log_4 3^2 – \frac{\log_4 2 + \log_4 3^3}{3\log_4 2} \)（←こちらで説明した対数の性質が使いやすい）
\(\displaystyle \quad = \log_4 2 + \log_4 3^2 – \frac{1}{3} – \frac{3\log_4 3}{3\log_4 2} \)
\(\displaystyle \quad = \log_4 2 + \log_4 3^2 – \frac{1}{3} – \frac{\log_4 3}{\log_4 2} \)
\(\displaystyle \quad = \log_4 2 + \log_4 3^2 – \frac{1}{3} – \log_2 3 \)（←底の変換公式を逆に使った）
\(\displaystyle \quad = \frac{\log_2 2}{\log_2 4} + \frac{\log_2 3^2}{\log_2 4} – \frac{1}{3} – \log_2 3 \)（←底2に揃えた）
\(\displaystyle \quad = \frac{1}{\log_2 2^2} + \frac{\log_2 3^2}{\log_2 2^2} – \frac{1}{3} – \log_2 3 \)
\(\displaystyle \quad = \frac{1}{2\log_2 2} + \frac{2\log_2 3}{2\log_2 2} – \frac{1}{3} – \log_2 3 \)
\(\displaystyle \quad = \frac{1}{2} + \log_2 3- \frac{1}{3} – \log_2 3 = \frac{1}{6} \)…（答）
たろぅちょっと複雑すぎるんですけど…。特に底の変換公式を逆に使う、なんて思いつきませんよ…。
確かに、かなり複雑な解答になってしまいました。
これは、元々の式の底4と底8を見たときに、\(4 = 2^2\)、\(8=2^3\)だから「どちらも２のべき乗になっている」ということを見抜けずに、単純に片方の底に揃えてしまったからです。
底を見比べて、なるべく共通な「指数の底（\(a^n\)の\(a\)も底という）」を見つけ出すことが重要です。
（解答２）
ということで、底4（\(=2^2\)）と底8（\(=2^3\)）に共通する指数の底2に揃えてみましょう。
\(\displaystyle \log_4 18 – \log_8 54 = \frac{\log_2 18}{\log_2 4} – \frac{\log_2 54}{\log_2 8} \)
\(\displaystyle \quad = \frac{\log_2 2 \cdot 3^2}{\log_2 2^2} – \frac{\log_2 2 \cdot 3^3}{\log_2 2^3} \)
\(\displaystyle \quad = \frac{\log_2 2 + 2\log_2 3}{2\log_2 2} – \frac{\log_2 2 + 3\log_2 3}{3\log_2 2} \)
\(\displaystyle \quad = \frac{1}{2} + \log_2 3 – \frac{1}{3} – \log_2 3= \frac{1}{6} \)…（答）
せんせこちらの方が解答がかなりスッキリしますね。
たろぅ確かに、これくらいなら計算できそう…。底を見比べて、共通な指数の底を見つけるのが重要なんですね。
実は指数関数にも底の変換公式がある
指数と対数を組み合わせた以下の性質は、実際の問題でもたまに使うことがあるので押さえておきましょう。
底が揃っているときの指数の対数乗の性質
\(a^{\log_a b} = b\)
「\(a^□\)の底\(a\)と指数部分の\(\log_a b\)の底\(a\)が一緒なら、値が、真数である\(b\)となる」
せんせこちらも例題を解いてみましょう。
例１．\(2^{\log_2 3} = 3\)
例２．\(9^{\log_3 5} = 3^{2 \log_3 5} = (3^{\log_3 5})^2 = 5^2=25\)
実際に問題を解く、くらいならこの性質を使うことができればOKです。
ですが、ここでは、この性質の別の面をもう少し深く掘り下げたいと思います。
\(a^{\log_a b} = b\)を\(b = a^{\log_a b}\)という形で見てみましょう。
これは、ある\(b\)に\(\log\)をつけてしまえば、好きな\(a\)を使って\(a^{\log_a b}\)の形にできる、ということです。
先ほどの例１で言えば、\(3 = 2^{\log_2 3}\)とみることで、\(3\)を\(2^{\log_2 3}\)の形に変換しています。
せんせもちろん、底2である\(2^{\log_2 3}\)の形じゃなくても大丈夫ですよね？
「3という値を変換する」という意味では、例えば適当に「底5」の形にしてもOKです。
\(3 = 5^{\log_5 3}\)
底10でもいけます。
\(3 = 10^{\log_{10} 3}\)
こんな感じで、ある\(b\)を、好きな底\(a\)を使って指数の形\(a^{\log_a b}\)にすることができます。
せんせ今度は、そもそもの\(b\)が指数の形になっているケースを考えてみましょう。
例えば、\(b=2^{100}\)としましょう。
底5の形にしてみます。
\(2^{100} = 5^{\log_5 2^{100}}\)
いいですよね？底10の形にしてみます。
\(2^{100} = 10^{\log_{10} 2^{100}}\)
これもOKですよね？
要はこの性質を使って、「底2の100乗」を「底5」や「底10」に変換しています。
つまり、この性質は「指数の底の変換公式」と捉えることができます。
このブログで活躍している「クマ」のLINEスタンプもあるよ！ぜひ見てください！
で？結局底の変換公式ってなんなの？
対数関数\(y=\log_2 x\)について考えてみましょう。
これを底の変換公式を使って、底3に変換することができます。
\(\displaystyle y=\log_2 x = \frac{\log_3 x}{\log_3 2} =\frac{1}{\log_3 2} \log_3 x\)
これは、\(y=\log_2 x\)は\(y=\log_3 x\)を\(\displaystyle \frac{1}{\log_3 2}\)倍したもの、とみることができます。
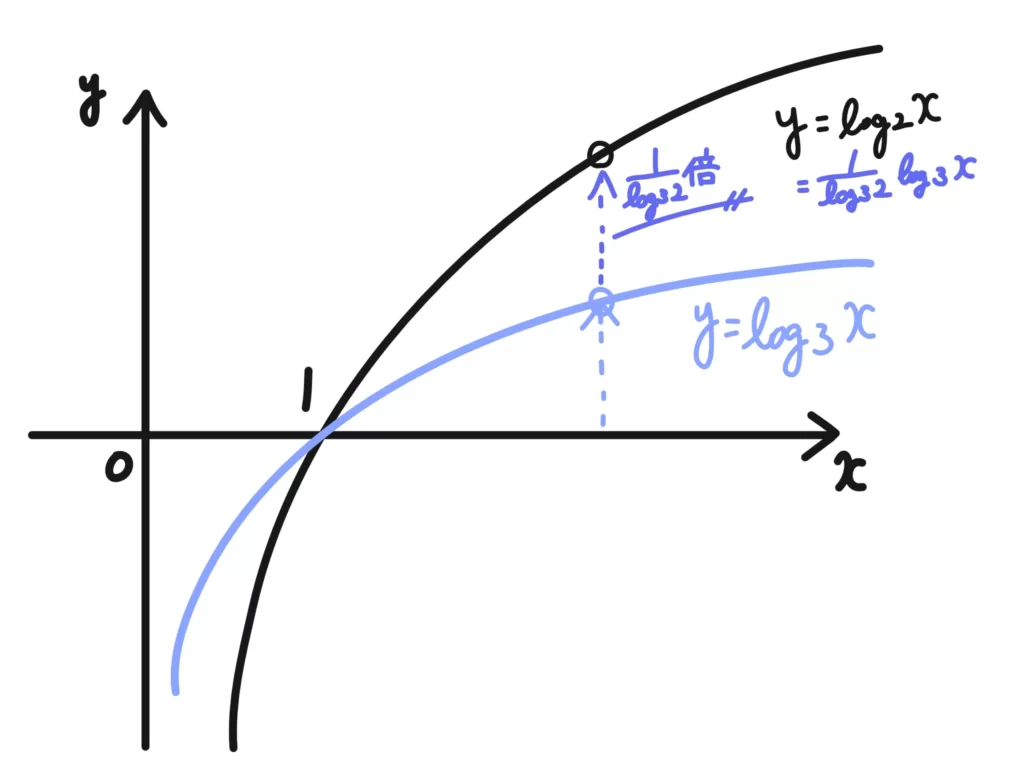
つまり、底の変換公式は「好きな底での値（や関数）」を補正して、元の値（や関数）の値を求める公式、といえます。
指数の底の変換もイメージ的には同じです。
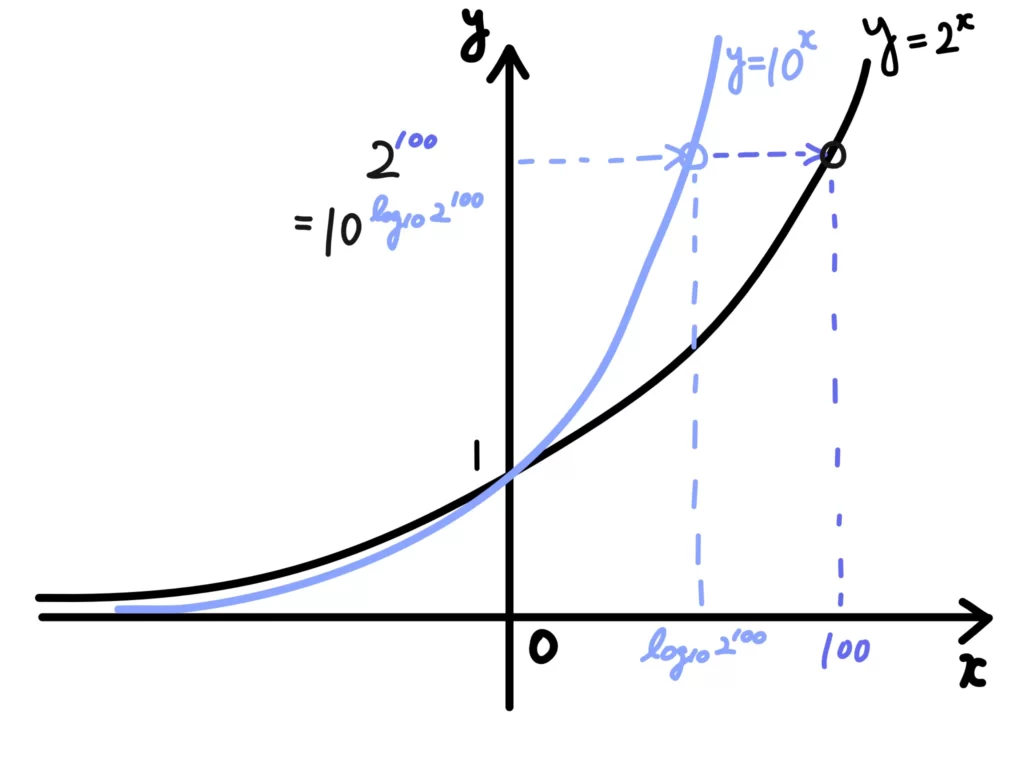
例えば、どんな指数関数でも、自然対数の底eを底とした\(y=e^x\)の形に変換できるのは数学的に大きな意味があります。
せんせ統計でも正規分布で\(y=e^x\)の形を使いますしね。（本当はもっと複雑な形だけど）
勉強が終わったらちょっと一息…Youtubeもやってます！バイクで走りながら大分を楽しく紹介中！ぜひご覧ください。
まとめ
対数の底の変換公式についてまとめました。
まずは、底の変換公式が使えることが重要です。
ですが、指数の底の変換公式も含めて、意味合いまで押さえておくと、変換公式のイメージが湧きやすいかなと思いますので、しっかりと本質を理解していきましょう。
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
