PR
対数とは？基本的な公式と本質を説明
対数関数は指数関数に比べて「そもそもなにこれ？よくわかんない…」という人が多いと思います。
この記事では、対数関数の基本的な公式（性質）とその本質的な意味を説明していきます。
目次
対数とは？
たろぅせんせい！対数ってなんですか？なんなんですか、アレ！？形も複雑だし、全く意味がわかりません！
せんせそうですよね。
たろぅむ…なんですか、その「どうせお前なんかわかんないだろ？」的なリアクション。
せんせまぁそうじゃなくて、対数っていきなり\(\log\)とか底とか出てきて複雑だし、何してるかわかりにくいので、最初から「わからん！」ってなる人が多いんですよ。
たろぅなぁんだ、そうなんですね。じゃあ詳しく教えてください！
せんせまぁ、たろうくんがそう言ってくるのは想定済みですけどね。
たろぅん？やっぱり「わかんないだろ？」って思ってました？
ということで、まずは対数の意味を説明していきます。
せんせそれでは質問です。\(2^x=8\)のとき、\(x\)の値は？
たろぅそんなの簡単ですよ。\(2^x=2^3\)ですから、\(x=3\)です。
せんせ正解です。では、\(2^x=32\)のとき、\(x\)の値は？
たろぅ\(2^x=2^5\)ですから、\(x=5\)です。
せんせ正解。じゃあ、\(2^x=5\)のとき、\(x\)の値は？
たろぅん？あら？\(5\)は\(2^x\)の形で表せないですよね？こんな\(x\)ってないんじゃないですか？
せんせじゃあこの図を見てください。
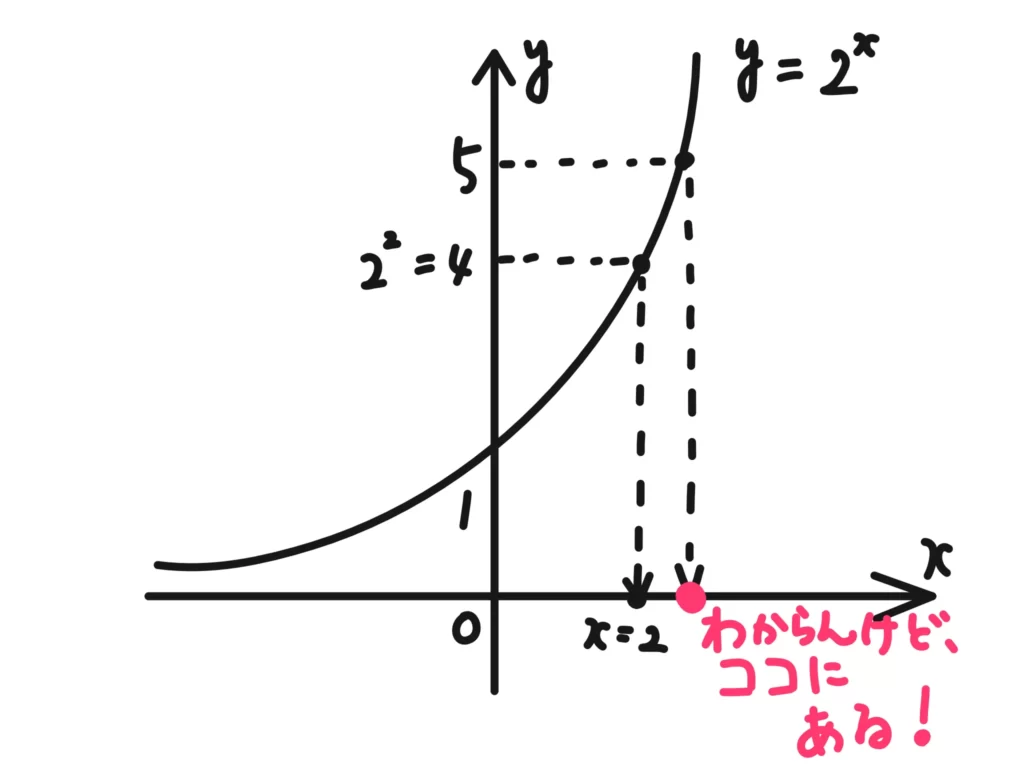
たろぅ…ありますね。でもこんな値ってどう表すんですか？
そうです、この値はどうやら存在するようですが、\(2^x=5\)を満たす\(x\)の値を表現する方法がありません。ここで出てくる表現方法が対数です。
「このときの\(2^x=5\)を満たす\(x\)を、\(x = \log_2 5\)と書くようにしよう」と決めたのが対数です。
一般的な文字で対数の定義を表現すると次のようになります。
対数の定義
\(a > 0, a \neq 1\)，\(c>0\)とすると、
\(a^b = M\) \(\Leftrightarrow\) \( \log_a M = b \)
ちなみに\(a\)のことを「底」といい、\( \log_a M\)の\(M\)を「真数」といいます。
せんせこの定義、なかなか覚えにくいです。
定義を覚えるために重要なのは、
①「底」は指数も対数も同じもの。
②対数は指数部分を表す。
この２点を押さえることですね。
①指数の形、\(a^b\)の\(a\)の部分を「底」といいます。一方、対数の形、\( \log_a M\)の\(a\)も「底」といいます。当然二つは同じものです。定義を使って変形するとき「ここは同じもの」と思っておくといいです。
②そもそもの話を思い出してもらえればわかりますが（先程の例で言えば、\(2^x=5\)の\(x\)を表現する方法として\(x=\log_2 5\)という対数を定義しました。）、「対数は指数部分を表す」という意識が重要です。
つまり、さっきの定義の話で言うと「\(\log_a M\)という対数は\(a^b\)の指数部分を表す」ということです。よって、\(\log_a M =b\)（\(b\)は指数部分）となります。
対数の公式（性質）
指数について、どんな底\(a\)でも以下の式が成り立ちます。
\(a^1 = a\)、\(a^0 = 1\)
これを対数の定義を使って変形すると、真数が\(a\)、1のとき対数は次のような値になります。
真数が\(a\)（底と一致）、1のときの対数の値
- \( \log_a a = 1\)
- \( \log_a 1 = 0\)
また、対数の基本的な性質として、次の３つがあります。よく使うので覚えておきましょう。
- \( \log_a bc = \log_a b + \log_a c\) … ①
- \( \displaystyle \log_a \frac{b}{c} = \log_a b – \log_a c\) … ②
- \( \log_a b^c = c \log_a b \) … ③
②は①とほぼ同じ証明、もしくは、①と③を使えば証明できるので、①と③の証明だけしておきます。
（①の証明）
右辺の\( \log_a b = k\)、\( \log_a c = l\)…【２式】とおく。対数の定義を使って変形すると、
\( a^k = b\)、\( a^l = c\)となります。
これらの式を両辺掛け合わせると、
\(a^k \times a^l = bc\)
\(a^{k+l} = bc \)
この式を対数の定義を使って変形すると、
\( \log_a bc = k+l\)
【２式】を使うと、
\( \log_a bc = \log_a b + \log_a c\) （終）
（③の証明）
\( \log_a b = k\)…【この式】とおきます。対数の定義を使って変形すると、
\( a^k = b\)
両辺を\(c\)乗して、
\( \{ a^k \}^c = b^c \)
\( a^{kc} = b^c \)
対数の定義を使って変形すると、
\( \log_a b^c = kc\)
【この式】を使うと、
\( \log_a b^c = c \log_a b \)（終）
対数の本質
たろぅんー…定義とか性質とかは、まぁわかったというか、覚えた感じですけど…。でも結局対数ってなんなのか、複雑に見えるだけでよくわかんないんですけど。
せんせじゃあ、対数の本質について説明しましょうか。
結論から言うと、先ほど説明した通り、対数の本質は「指数部分」です。
例えば、\( \log_a bc = \log_a b + \log_a c\)という性質についても、
\(b \times c\)の指数部分は\(b\)の指数部分と\(c\)の指数部分を足したもの
と読み替えることができます。これは後述する指数法則を、対数の形で言い換えたものになります。（上の説明は若干言葉足らずですが、対数は指数部分の話をしているんだ、というところが掴めればOKです。）
また、指数法則を思い出してくれたらわかるのですが、掛け算・累乗の計算は、指数部分の足し算・掛け算で計算することができます。
指数法則
- \( a^m \times a^n = a^{m+n}\) ←掛け算が、指数部分の計算で言うと足し算に変換される。
- \( (a^m)^n = a^{mn}\)←累乗が、指数部分の計算で言うと掛け算に変換される。
つまり、対数（＝指数部分）で考えることで、掛け算を足し算に、累乗を掛け算に変換することができ、計算が容易になります。
ここでは詳しく触れませんが、対数を使えば「\(2^{100}\)は何桁の数？最高位の数はいくつ？」などという問題も解くことがでます。このように、ものすごく大きい（小さい）計算結果のおよその値を調べて把握するときに役に立ちます。
まとめ
対数関数の基本的な公式や本質的な考え方について説明しました。
公式は覚えておいてもらいたいですが、その本質である、
「対数とは、指数部分を表したものである」
ことと、
「対数計算により、（指数との橋渡しをすることで）指数計算を簡単にすることができる」
ことを押さえておいてください。
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
