PR
数列の基本!等差数列を基礎から徹底的に解説【公式の覚え方のイメージも】

数列の基本、等差数列…。
基本ではあるのですが、数列は公式が複雑になりがちです。
この記事では、等差数列の基本と公式のイメージを図を使いながら説明していきます。
 デカ丸
デカ丸公式も原理をイメージするだけで覚えやすくなるよ
等差数列とは?



はい、じゃあこの生徒会で集めた募金を数えるのよ。



うっ…!(全部1円…1円の山…)



さ、早く数えて。



…はい。2、4、6、8、10円…っと。
(1時間経過…)



うぅ…やっと10円の束にしたぞ。じゃあこれを数えて…10、20、30、40…。



まだですかぁ?はやくしてくださーい。
ということで、等差数列です。
2、4、6、8…とか10、20、30、40…とよく数えますよね。
このように、ある一定の数ずつ増えていく(もしくは減っていく)数列のことを等差数列といいます。
上の例は2ずつ増えたり、10ずつ増えていくので等差数列と言えます。
もう少し数学的に言うと、等差数列は「前の項に、ある一定の数を足すことで次の項が得られる数列」です。
等差数列を決定するのは、初項\(a\)と足していく「一定の数」\(d\)です。この「一定の数」のことを公差といいます。
等差数列は数列の基本です。公式や重要なイメージを確認していきましょう!
等差数列の一般項の公式
等差数列の一般項(第\(n\)番目の項)は次のようになります。
等差数列の一般項
初項\(a\)、公差\(d\)の等差数列\( \{ a_n \} \)の一般項\(a_n\)は、
\(a_n = a + (n-1)d\)



公差\(d\)に掛かるのが\( (n-1) \)というところがポイントですね!
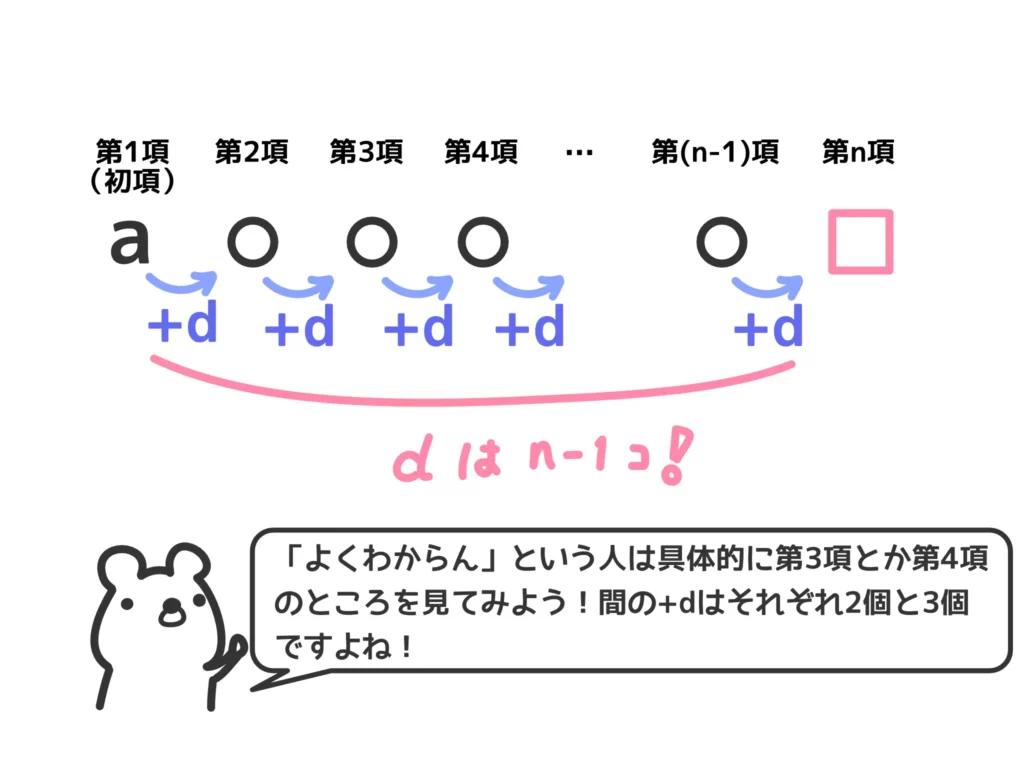

一般項(第\(n\)番目の項)は\(a_n = a + d +d +d +\cdots + d = a + (n-1)d\)と計算できます。
一般項\(a_n\)を出しておけば、\(n\)に必要な数や文字を代入することで、すぐに「第◯項」を求めることができるので、数列において一般項を求める作業はかなり重要です。
ちなみに「等差数列の一般項を求めなさい」という問題を出したら、式整理をしない人がたまにいるんですよね…式整理はしてください。
例.初項2、公差3の等差数列の一般項は、\(a_n = 2 + (n-1)3\)(←ここで終わらせない)。よって、\(a_n=3n-1\)(←ここまで整理する。)
等差数列の「等差」は「差が等しい」という意味です。
公差\(d\)の等差数列では、どんな自然数\(n\)に対しても、\(a_n\)と\(a_{n+1}\)の間には次のような関係が成り立っています。
\(a_{n+1} = a_n + d\) …※
\(a_{n+1} – a_n = d\)



ということで、隣の項との差が常に等しい数列ということがわかります。
こういう書き方をすると「よくわかんない…」という人がいるかもしれませんが、数列では抽象的な「\(n\)番目」とか「\((n+1)\)番目」のような表現をすることが多いので、少しずつ慣れていきましょう。
ちなみに後々出てきますが、数列を※のように式で表したものを漸化式といいます。
等差数列の和の公式
数列では、初項から第\(n\)項までの和もよく求めます。
例.\(\displaystyle 1 + 2 + 3 + \cdots +n = \frac{1}{2}n(n+1) \)など。(←なぜこうなるかは後ほど)
等差数列の第\(n\)項までの和の公式は次のようになります。
等差数列の和
初項\(a\)、末項\(l\)、項数\(n\)の等差数列\( \{ a_n \} \)の和\(S_n\)は、
\(\displaystyle S_n = \frac{1}{2} n (a + l)\)…①
もしくは、初項\(a\)、公差\(d\)、項数\(n\)とすると、
\(\displaystyle S_n = \frac{1}{2} n \{ 2a + (n-1)d \} \)…②
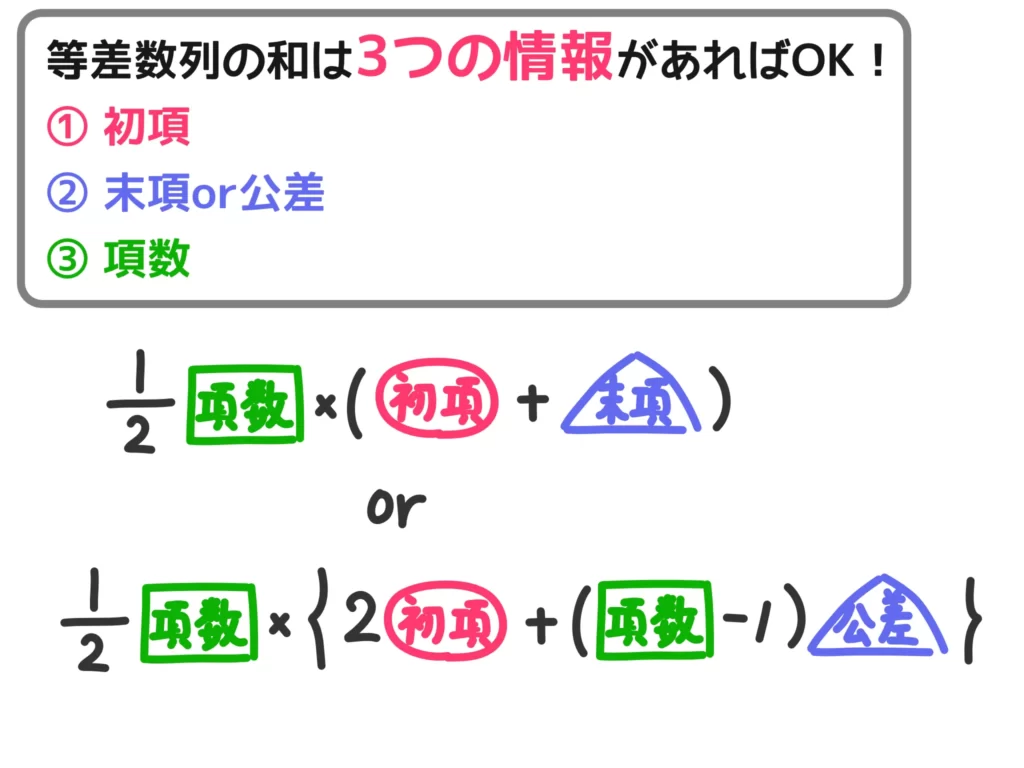




②の公式については、「\(2a\)」となるところが一般項の公式と違うので注意です。②は初項と公差(と項数)がわかれば使えるので便利がいい気がしますが、①の方が考え方としては本質的です。
(証明)
等差数列の「最初と最後」、「2番目と最後から2番目」…を足せば一定の値になる、というのは結構知っている人が多いですが、それをしちゃうと、項の数が偶数なのか?奇数なのか?によって処理方法が変わるのが悩みどころです。
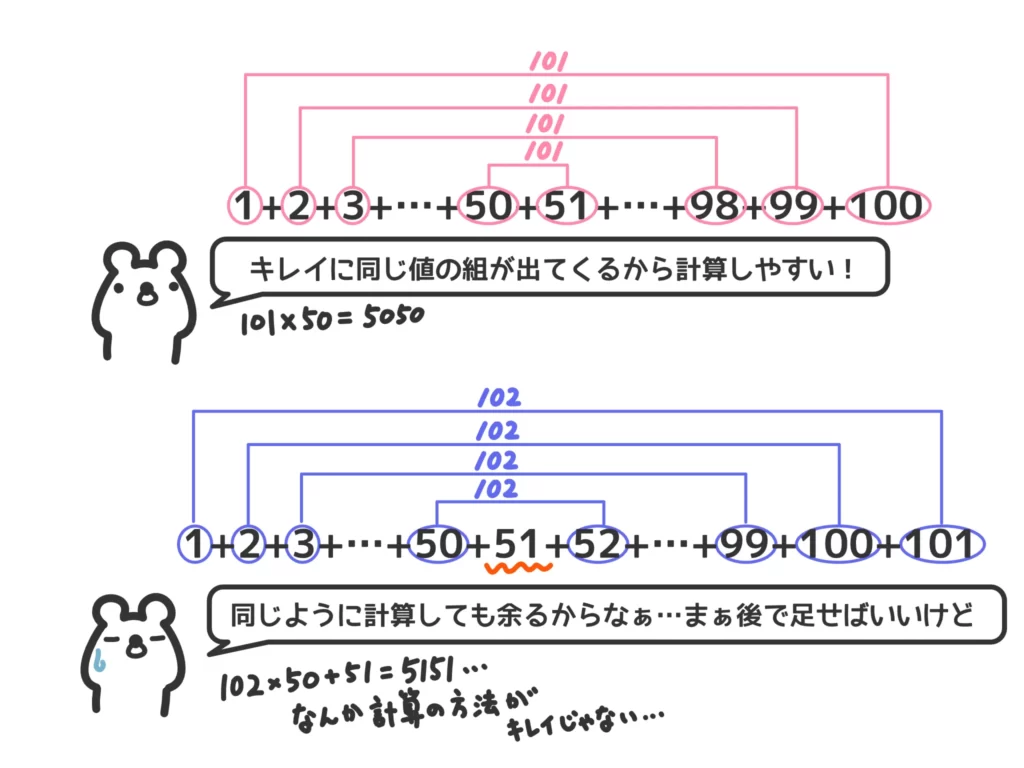

本当は「分かりやすい部分を計算して、分かりにくい部分はあとで付け加える」というのは数列の和の考え方としては重要なのですが、公式としては使いづらいので、証明としては\(S_n\)を2つ準備します。
\(S_n = a + (a+d) + (a+2d) + \cdots + (l-2d) + (l-d) + l \)…①
\(S_n = l + (l-d) + (l-2d) + \cdots + (a+2d) + (a+d) + a \)…②
\( (l-d) \)、\( (l-2d) \)のところがわかりにくいかもしれませんが、公差\(+d\)なので、末項から逆に数えると\(-d\)すればいいことになります。
加えて、②の形がポイントです。式としては①と同じですが、末項から逆の順番に並べています。
①+②より
\(2S_n = (a+l) + (a+l) + (a+l) + \cdots + (a+l) + (a+l) + (a+l) \)
\(2S_n = n(a+l)\)
\(\displaystyle S_n = \frac{1}{2}n(a+l)\)(終)
また、末項\(l\)はこの場合第\(n\)項のことなので、
\(l = a_n = a+ (n-1)d\)を代入すると、
\(\displaystyle S_n = \frac{1}{2} n \{ a + a + (n-1)d \} \)
よって、
\(\displaystyle S_n = \frac{1}{2} n \{ 2a + (n-1)d \} \)(終)
冒頭の\(\displaystyle 1 + 2 + 3 + \cdots +n = \frac{1}{2}n(n+1) \)は、
初項\(1\)、末項\(n\)、項数\(n\)の等差数列の和
と言えます。よって、公式を使うと、\(\displaystyle \frac{1}{2}n(1+n)=\frac{1}{2}n(1+n) \)となります。
問.初項4、公差3の等差数列の初項から第\(n\)項までの和\(S_n\)と、初項3、公差2の等差数列の初項から第\(n\)項までの和\(T_n\)の差\(S_n – T_n\)を求めよ。
答え
\(\displaystyle \frac{1}{2}n(n+1)\)
(解答は2パターンくらいあります)
まとめ
等差数列の基本と公式の確認でした。
特に公式は「覚えるのが苦手…」という人も多いです。
文字の羅列ではなく、イメージを押さえながら実際に使って覚えていきましょう。








