絶対値方程式・不等式の解き方まとめ【場合分けの「なぜ？」にも答えます】

2024年1月17日2024年4月29日

こちらの記事で絶対値の基本について説明しましたが、一番気になる絶対値方程式・不等式の話はほとんどしていませんでした。

せんせ

でも、こちらの記事の内容は押さえておいた方がいいです。絶対値の外し方と注意点について言及しています。

絶対値方程式・不等式の解き方

今回は茶番無しでいきます。

せんせ

早速絶対値方程式・不等式の解き方をまとめていきましょう！

ポイントは、

「絶対値方程式・不等式の右辺が定数か\(x\)の式か？によって解き方が変わる」

という点です。

ただし、「右辺」は絶対値がついていない、とします。もちろん両辺に絶対値がついていることもありますがそれはレベルの高い問題なので、とりあえず基本である片方の辺にのみ絶対値がついている、という状況で話を進めていきます。

絶対値の右辺が定数の場合

せんせ

右辺が定数の場合は決まり手があります

例1．\(x\)に関する方程式・不等式を解け。
(1) \( |x -2 | = 3\)
(2) \( |x+1| \geq 2\)
(3) \( |2x-1| < \sqrt{2}\)

右辺が定数の場合、機械的に解くことができます。

絶対値方程式・不等式【右辺が定数の場合】

\(a\)は\(a > 0\)を満たす定数とする。

・\( |x| = a \iff x = \pm a\)

・\( |x| > a \iff x < -a, a < x\)

・\( |x| < a \iff -a<x<a\)

ただし、不等式の場合、\(\geq\)のように「=」が付けば、答えにも「=」を付けます。

せんせ

特に不等式の答えの形が複雑に見えますが、この後習う、二次不等式でも同じ形の解になるので、ここで覚えておきましょう。
例1のように中身が単純な\(x\)でなくても、中身をひとまとまりとして同じように処理できます。

それでは先ほどの例1を解いてみましょう。

例1．
(1) \( |x -2 | = 3\)
(2) \( |x+1| \geq 2\)
(3) \( |2x-1| < \sqrt{2}\)

先ほどの結果に当てはめていけばOKです。

（解答）

(1) \( |x -2 | = 3\)より
　\( x-2 = \pm 3\)
　よって、\(x = -1, 5\)…（答）

(2) \( |x+1| \geq 2\)より
　\( x+1 \leq -2 , 2 \leq x+1\)　
　よって、\(x \leq -3 , 1 \leq x \)…（答）

(3) \( |2x-1| < \sqrt{2}\)より
　\( -\sqrt{2} < 2x-1 < \sqrt{2}\)
　\(\displaystyle \frac{1-\sqrt{2}}{2} < x < \frac{1+\sqrt{2}}{2}\)…（答）

せんせ

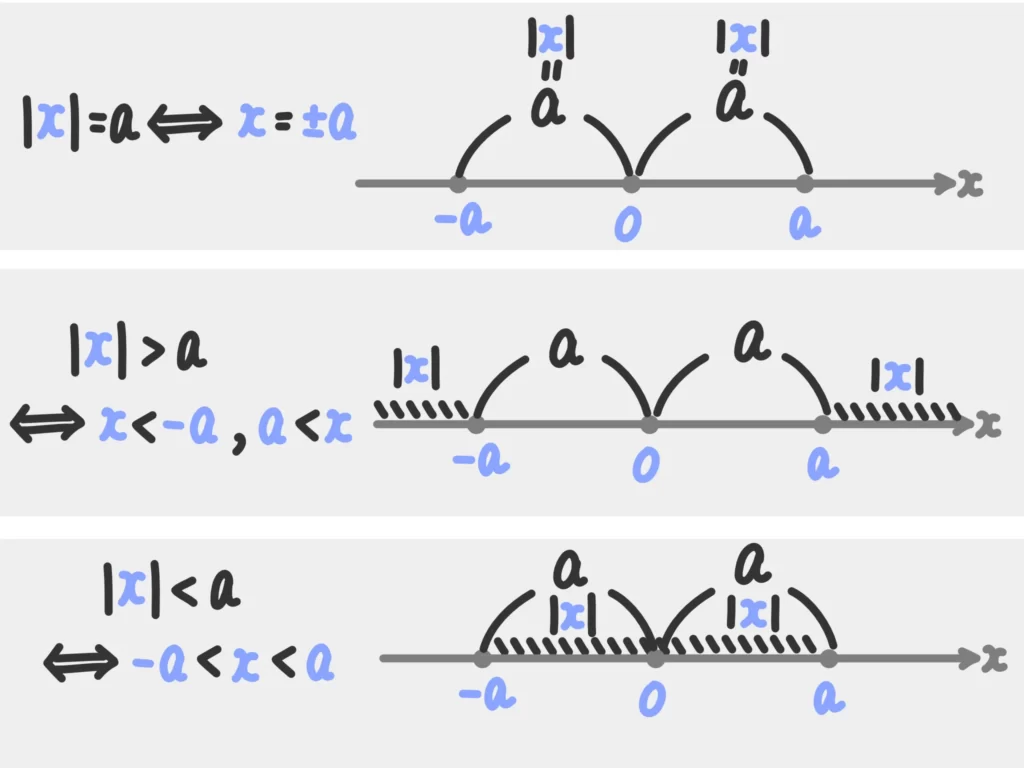
なぜ絶対値方程式・不等式があの形の解になるか？は次の図を見ていただければ、と思います。

絶対値の右辺がxの式の場合

右辺が\(x\)を含んだ式のときは場合分けをしましょう。というか、基本的に絶対値を外すときは場合分けをします。例えば、絶対値を含んだ関数のグラフをかくときも場合分けをします。

右辺が定数のときでも場合分けをしてくれても構いません。が、場合分けは面倒なので、できれば避けるべきです。場合分けをしなくていいときはしないにこしたことはないです。右辺が定数のときに場合分けをしなくていい理由は後ほど述べます。

せんせ

こういう書き方をすると「じゃあ色々考えるのが面倒だから全部場合分けすればいいじゃん」と考える人がいます。ですが、数学は条件によって解き方を変えるべきです。なるべく条件を丁寧に考えて、結果楽に解ける解法を選んでください。

では、どのように場合分けをするかというと、

「絶対値の中身が＋なのか？ー（マイナス）なのか？」

によって分けます。

絶対値の外し方（場合分け）

\( |x| = \begin{cases} x \quad (x \geq 0) \\ -x \quad (x < 0)\end{cases}\)

せんせ

\(\geq\)の「＝」はどちらにつけてもいいですが、まぁ普通\(\geq\)につけますね。

せんせ

絶対値の中身を無視して「\(x \geq 0\)と\(x < 0\)」で分ける人がいますが、必ず中身の＋ーで分けましょう！中身です！中身！

例2．\(x\)に関する方程式・不等式を解け。
(1) \( |x-1| = 2x+2 \)
(2) \( |2x+2| \leq -x \)

（解答）

(1) (i) \(x-1 \geq 0\)、つまり \(x \geq 1\)のとき
　　　\( x-1 = 2x+2 \)
　　　\( x = -3\)
　　　\( x \geq 1\)より不適。
　　(ii)\(x-1 < 0\)、つまり \(x < 1\)のとき
　　　\( -(x-1) = 2x+2 \)
　　　\(\displaystyle x = -\frac{1}{3}\)（これは\(x < 1\)を満たす。）
　　以上(i)(ii)より\(\displaystyle x = -\frac{1}{3}\)…（答）

(2) (i) \(2x+2 \geq 0\)、つまり\(x \geq -1\)のとき
　　　\( 2x+2 \leq -x \)
　　　\(\displaystyle x \leq -\frac{2}{3}\)
　　　\(x \geq -1\)より\(\displaystyle -1 \leq x \leq -\frac{2}{3}\)
　　(ii)\(2x+2 < 0\)、つまり\(x < -1\)のとき
　　　\( -(2x+2) \leq -x \)
　　　\(\displaystyle x \geq -2\)
　　　\(x < -1\)より、\( -2 \leq x < -1\)
　　以上(i)(ii)より\(\displaystyle -2 \leq x \leq -\frac{2}{3}\)…（答）

せんせ

もう一度まとめておきます。右辺が定数の場合は機械的に、そうでなければ場合分けが基本です！

絶対値方程式・不等式【右辺が定数の場合】

\(a\)は\(a > 0\)を満たす定数とする。

・\( |x| = a \iff x = \pm a\)

・\( |x| > a \iff x < -a, a < x\)

・\( |x| < a \iff -a<x<a\)

ただし、不等式の場合、\(\geq\)のように「=」が付けば、答えにも「=」を付けます。

絶対値の外し方【場合分け】

\( |x| = \begin{cases} x \quad (x \geq 0) \\ -x \quad (x < 0)\end{cases}\)

「とりあえず解き方がわかればいいよ」という人はここまででOKです。

ここからは「絶対値を外すときに場合分けをしたりしなかったり…なんとなく腑に落ちないなぁ」というひとはぜひ読んでみてください。

絶対値方程式・不等式の場合分けの「なぜ？」

こうやって解き方をまとめると、

たろぅ

絶対値の方程式とか不等式は、なんで場合分けが必要だったり必要じゃなかったりするんじゃい…。

と思うかもしれません。

せんせ

ここでは絶対値の場合分けの「なんでじゃい！」を少し深く掘り下げてみたいと思います。

絶対値の右辺が定数のときなぜ場合分けがいらないのか？

絶対値の処理をする問題をたくさん解いていくとわかりますが、ほとんどの場合、中身の＋ー（マイナス）によって場合分けをします。

そこで思うのが、

たろぅ

なんで右辺が定数だったときは場合分けをしないんだろう…。

という疑問ですね。

せんせ

まずは、右辺が定数のときの問題を場合分けして解いてみましょう。

例1．(1) \( |x -2 | = 3\)

の解答について。

　\( x-2 = \pm 3\)

としますが、場合分けしようとすると、

(i) \(x-2 \geq 0\)、つまり\(x \geq 2\)のとき
　\( x-2 = 3\)
　\(x = 5\)（これは\(x \geq 2\)を満たす）
(ii) \(x-2 < 0\)、つまり\(x < 2\)のとき
　\( -(x-2) = 3\)
　\(x = -1\)（これは\(x < 2\)を満たす）

となります。

せんせ

ここで、場合分けの条件とそのときの式を見てましょう。

(i) \(x-2 \geq 0\)、つまり\(x \geq 2\)のとき
　\( x-2 = 3\)

…これ、よく見てみると、当たり前じゃないですか？

「\(x-2 \geq 0\)のとき、\( x-2 = 3\)」。この答え\(x=5\)は当然\(x-2=3\)を満たしますが、右辺が\(3(>0)\)なら、それと等しい左辺の\(x-2\)も当然\(x-2>0\)となりますよね？

つまり、「（中身）＝正の値」という式から出てきた答えが、「（中身）が0以上のとき」という条件を満たすのは当たり前なんです。

同様に、

(ii) \(x-2 < 0\)、つまり\(x < 2\)のとき
　\( -(x-2) = 3\)

は\(x-2 = -3\)とすると話が見えやすいです。このとき、「（中身）＝負の値」という式から出てきた答えが「（中身）が負のとき」という条件を満たすのは当たり前ですよね。

せんせ

不等式のときも同じように考えることができます。一度考えてみてください！

ということで、右辺が定数のときは場合分けの必要がないんです。

おまけ１．絶対値の右辺が負の値？

教科書も問題集もあえて触れていませんが、例えば

\( |x-2| = -3\)

などという問題はありません。

仮に出たとしても、

たろぅ

右辺定数やぁ！±つけりゃOKじゃあ！

（解答）
\( x-2 = \mp 3\)よって、\(x =-1, 5\)

と答えてはいけません。

なぜなら、\( |x-2| = -3\)という式を満たす\(x\)はあり得ないからです。どんな\(x\)でも「（絶対値）=負の値」となることはありませんよね？

ということで「（絶対値）=負の値」という形の方程式は明らかに「解なし」となり、問題として成り立たない（というか、面白くない上に無駄に間違える可能性がある）ので、この形の問題はないんですね。

せんせ

ちなみにグラフを使っても確認することができます。

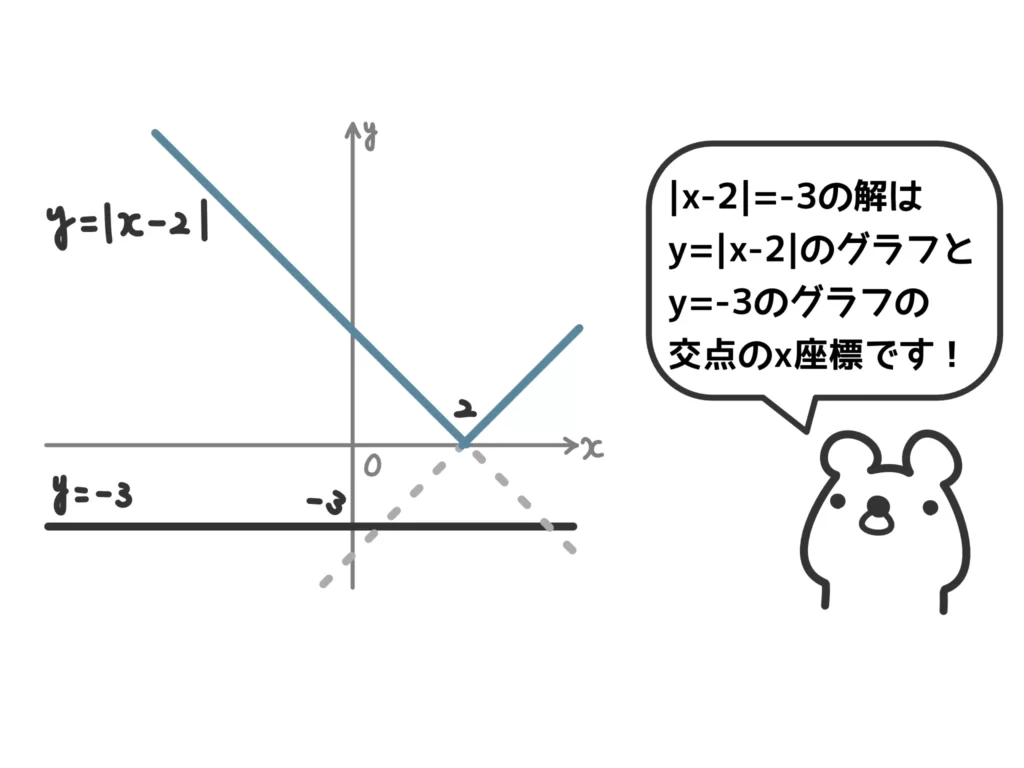
絶対値の右辺がxの式のときなぜ場合分けが必要なのか？

ここまでの話がわかっていれば、右辺に\(x\)の式があるときは単純に＋ーを付けて計算してはいけない、というのがわかると思います。

なぜなら、右辺が\(x\)の式のとき、右辺は負の値になる可能性があるからです。

せんせ

例をもう一度見て確認してみましょう。

例2．(1) \( |x-1| = 2x+2 \)

（解答）
(i) \(x-1 \geq 0\)、つまり \(x \geq 1\)のとき
　　\( x-1 = 2x+2 \)
　　\( x = -3\)
　　\( x \geq 1\)より不適。
…

となりますが、このとき（右辺）=\(2(-3)+2 = -4\)となり、負の値になります。先程の「おまけ．絶対値の右辺が負の値？」のときに確認しましたが、これを満たす\(x\)は本来ありえません。

たろぅ

じゃあこの答えってなんなの？

せんせ

これも、グラフを使えば正体がわかりやすいです！

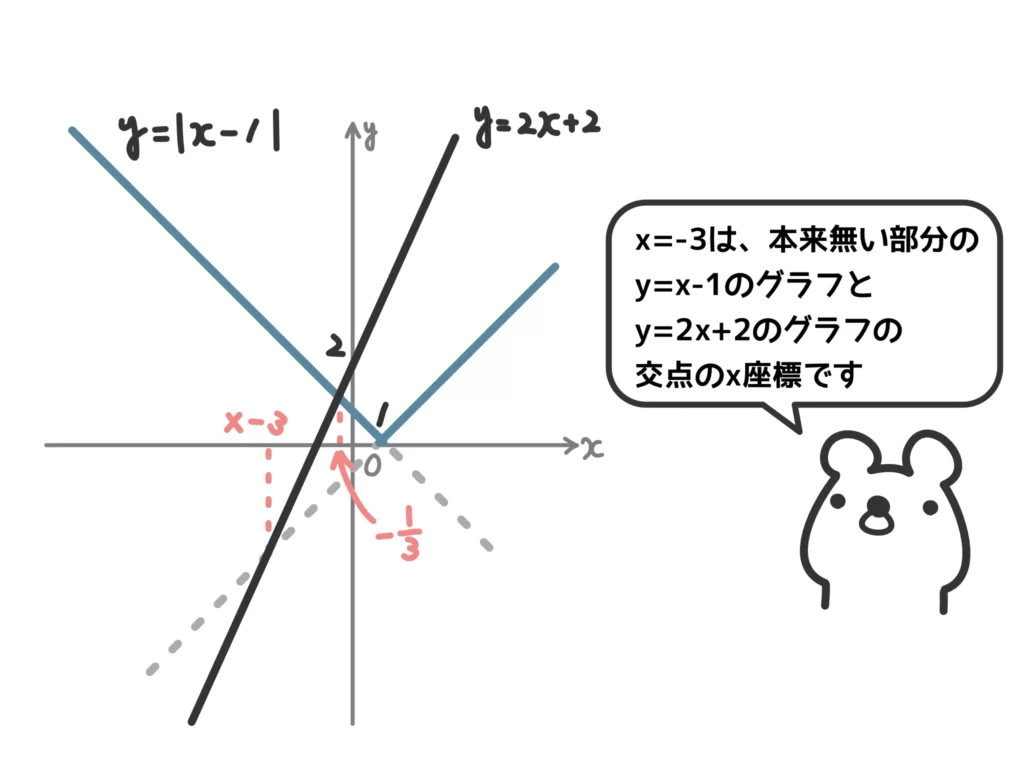
ということで、「仮にそのままグラフを伸ばしたときに出てくる交点」なんです。当然、\(x\)の適切な範囲に入ってこないので不適になります。

おまけ２．絶対値方程式の右辺が0以上のxの式のとき

じゃあ右辺が0以上であることが保証された\(x\)の式であるとき、場合分けをしなくていいか…と言われると、正直やめたほうがいいです。

絶対値の中身による場合分けをしなくても（\(x\)の範囲を考えなくても）解けますが、「場合分けをしなくていいのは右辺が定数のとき」という認識が一般的ですし、仮に場合分けをしないならその理由を説明しないといけないので…まぁ、右辺が\(x\)の式のときは場合分けをしておくのが無難ですね。

練習問題1-4【No.12】

問．次の\(x\)に関する方程式を解け。

\( | 2x+1 | = x^2\)

答え

\(x = -1, 1 \pm \sqrt{2}\)

練習問題の模範解答も販売中！

１分野２００円なので、解答が欲しい分野だけ格安で購入できます！！

別解や思考方法、注意点、補足説明など、note記事だからできる、他にはなかなか無い模範解答に仕上がっています。

絶対値方程式・不等式のまとめ

絶対値方程式・不等式の解き方のまとめでした。

絶対値の中身による場合分けについても詳しく説明したので、疑問に感じている部分はじっくりと読んでみてください。