二次不等式の解き方のポイントは？【判別式を使うのってどういうとき？】

2024年1月6日2024年4月29日

二次不等式…。

基本的な解き方も結構複雑ですし、その上「すべての実数」や「解なし」といった解まで出てきて、

たろぅ

お腹いっぱい…いや、お腹イタい…。

となりがちな部分です。

でも大丈夫。実はごく基本的なポイントさえ押さえていれば、あとは自然と解けるんです。

この記事では二次不等式の基本的な解き方のポイントとパターンについて丁寧に解説していきます。

二次不等式の解き方の基本

たろぅ

あぁ！二次不等式の解き方がわからない！

はなこ

…。

たろぅ

なんであんなに複雑なんだ！しまいには「すべての実数」が答え？「解なし」が答えだと！？「解なし」が解ってなんだ！一休さんか！？

せんせ

…。

たろぅ

誰か、わかりやすく教えてくれないかなぁ！

ということで、二次不等式です。

いつもの茶番は何も思い浮かびませんでした…スイマセン。ですが、確かに「解なし」が解って変ですよね。

この二次不等式は解のパターンがかなりあるので「わけわからん…」となる人もいますが、ポイントを押さえておけば大丈夫です！

せんせ

その代わり、後で説明しますが、その都度グラフを使って判断することになります。

まずは次の問題を解くことを考えてみましょう。

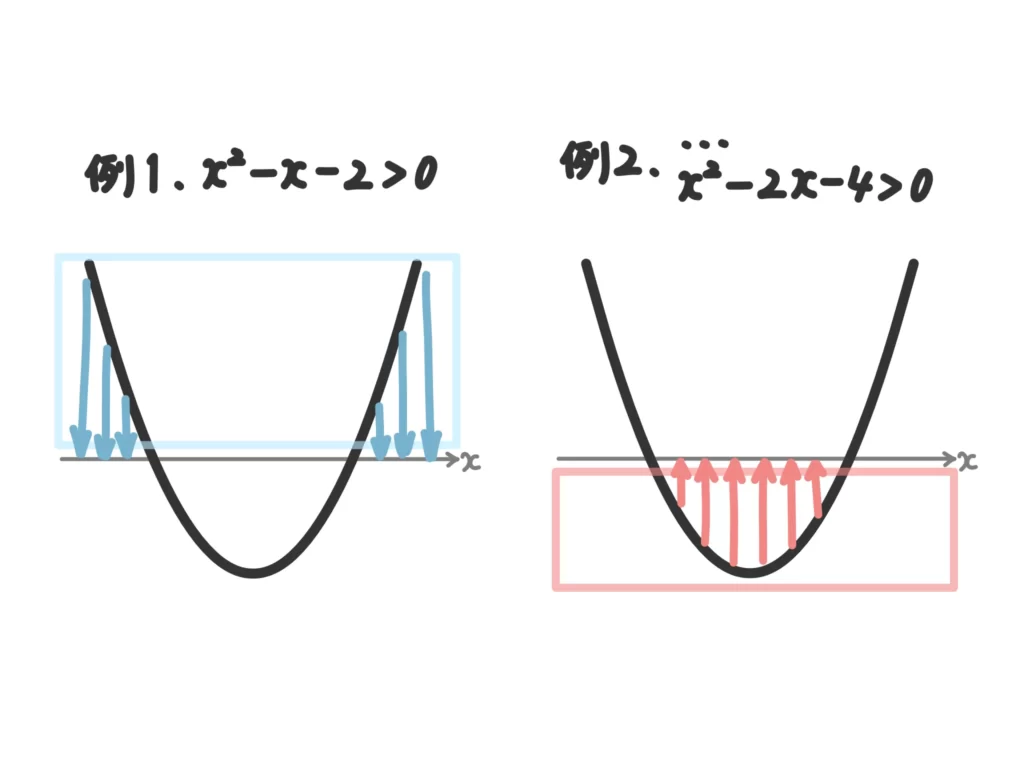
例1．\(x\)に関する不等式\( x^2-x-2 > 0\)を解け。

例2．\(x\)に関する不等式\( -x^2+2x+4 \geq 0\)を解け。

二次不等式を解くには「関数」がポイント？

いきなりですが、二次不等式を解く際の最大のポイントはグラフをイメージすることと、不等式の意味を押さえることです。

その都度グラフを使って判断といいましたが、あくまで「不等式を解く」ことが目的なので、ある程度ルーティンワークが必要になってきます。

せんせ

特に、下に凸と上に凸がゴチャゴチャすると判断がしにくいので、\(x^2\)の係数のー（マイナス）は払って、下に凸のグラフに統一して考えるようにしましょう。

ということで、例2のような\( -x^2+2x+4 \geq 0\)は左辺の\(x^2\)の係数がー（マイナス）なので、払っておきます。

\(-1\)を両辺に掛けると\( x^2-2x-4 \leq 0\)となります。不等式の両辺にー（マイナス）を掛けるので、不等号の向きが変わることに注意してください。

この状態で、左辺を\(y=\)とみなし、グラフと不等式の意味を考えます。

例1では、\( (y=)x^2-x-2 > 0\)となるので、「グラフの\(y>0\)となる\(x\)の範囲は？」という意味になります。

例2では、\( (y=)x^2-2x-4 \leq 0\)となるので、「グラフの\(y \leq 0\)となる\(x\)の範囲は？」という意味になります。

でも結局二次不等式を解くには「＝０」の答えが必要

このグラフのイメージができれば、あとはグラフと\(x\)軸の交点の\(x\)座標が必要となることがわかります。

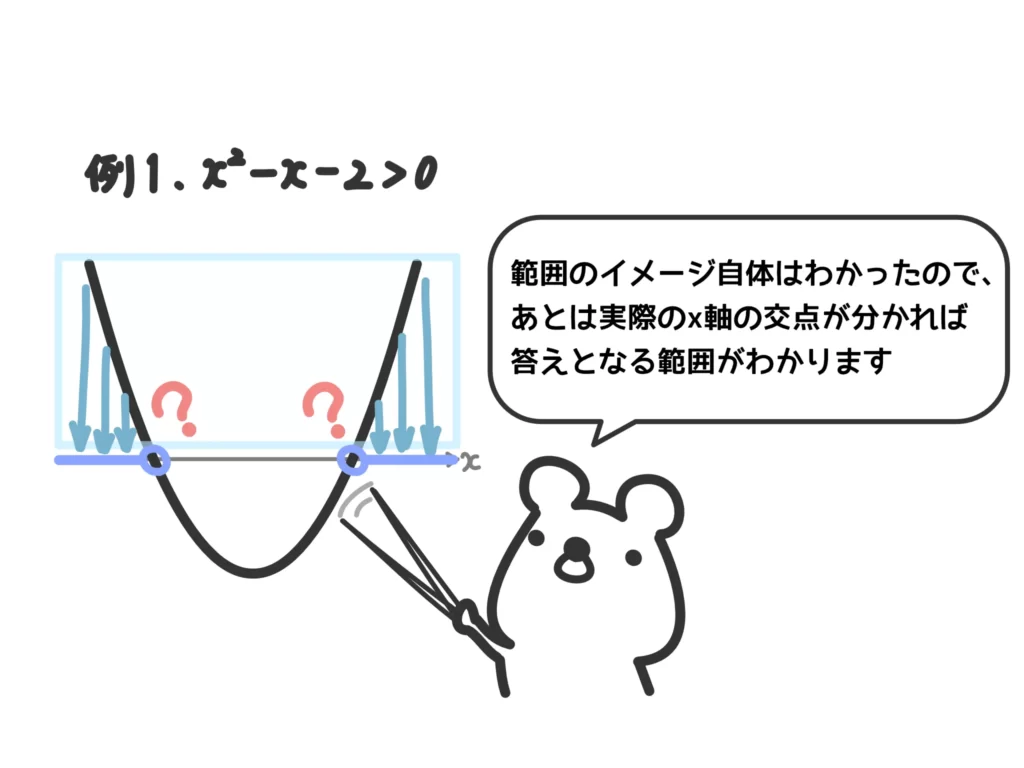
つまり、この\(x\)座標を求めるには、因数分解もしくは解の公式を使うなどして（左辺）=0としたときの方程式の解を求めなければいけません。

ということで、

例1であれば、\(x^2-x-2 = 0\)としたとき、因数分解して\( (x+1)(x-2)=0\)、つまり\(x = -1,2\)。

例2であれば\(x^2-2x-4 = 0\)としたとき、解の公式を使って\( x = 1 \pm \sqrt{5}\)。

よって、

例1の解は\(x < -1, 2 < x\)、

例2の解は\(1-\sqrt{5} < x < 1+ \sqrt{5}\)となります。

二次不等式の解き方まとめ

せんせ

一度、二次不等式の解き方をまとめておきます。

二次不等式の解き方まとめ

二次関数のグラフを利用する。解き方に統一性を持たせるために\(x^2\)の係数は＋にしておき、下に凸のグラフで考える。
不等式の意味を押さえておく。「\(x\)軸より上にある部分？」か「\(x\)軸より下にある部分？」のどちらを聞かれているかを判断する。
（左辺）=0としたときの解を求める。この結果と②を合わせて\(x\)の範囲を求める。

\(a>0\)、\(\alpha < \beta\)としたとき、

\(a(x-\alpha)(x-\beta)>0\)　→　\(x < \alpha , \beta < x\)
\(a(x-\alpha)(x-\beta)<0\)　→　\(\alpha < x < \beta\)

の答えの形は、グラフをイメージしながらサッと書けるようにしておきましょう。

（\(\geq, \leq\)の場合は、そのまま答えの不等号に「＝」が追加されるだけです。）

せんせ

ただ、二次不等式は本質的に「考え方→答えの判断」を全て二次関数のグラフに置き換えているので、解答が書きづらいです。「このくらい書いとけばいいかな」という解答例も載せておきます。

例1．\(x\)に関する不等式\( x^2-x-2 > 0\)を解け。

グラフの形は頭に描きつつ、実際は次の解答程度で十分です。

（解答）

\( x^2-x-2 > 0\)より

\((x+1)(x-2) > 0\)

よって\( x < -1, 2<x\)…（答）

せんせ

ひとつ注意点としては、必ず
\( x < -1, 2<x\)
の形で書くようにしましょう。
\( x < -1, x>2\)と書く人がいるのですが、
不等式が２つ並ぶ＆「<」「>」が入り乱れるので間違いやすい、というのと、
\( x < -1, 2<x\)の形の方がグラフのイメージと一致する
ので、こちらで書くようにしてください。

例2．\(x\)に関する不等式\( -x^2+2x+4 \geq 0\)を解け。

これはちょっと微妙です…。一応丁寧に書いておきます。

（解答）

\( -x^2+2x+4 \geq 0\)より、

\( x^2-2x-4 \leq 0\)

\( x^2-2x-4 = 0\)とすると、\( x = 1 \pm \sqrt{5}\)

よって、\(1-\sqrt{5} < x < 1+ \sqrt{5}\)…（答）

個人的な意見ですが、

\( -x^2+2x+4 \geq 0\)より、

\( x^2-2x-4 \leq 0\)

よって、\(1-\sqrt{5} < x < 1+ \sqrt{5}\)…（答）

くらいでもいいと思っています。

せんせ

おいおいおい…この\(1 \pm \sqrt{5}\)はどこから来たんだい？

とツッコまれそうな気もします。

確かにそうなんですが、私は二次不等式はとりあえず解ければいいと思っていますし、実際、問題のレベルが上がれば二次不等式を解くこと自体はその問題のほんの一部である、ということも多いです。

二次不等式は「考え方はグラフでしっかり、解答はシンプルに」という方がいいのではないか、と思っています。

せんせ

テストで✕くらうのが不安だったら担当の先生に聞いてみてね。

二次不等式と判別式「すべての実数」「解なし」？

たろぅ

あー…やられた…。アレだ、ニセモノを掴まされるとはまさにこのことだね。

はなこ

ん？どしたの？

たろぅ

言われた通りにやったけど、この問題、グラフをイメージするまではいいけど、「=0」としたときの解がないじゃん！これじゃ解けねぇぜ！「解なし」だ！

例3．\(x\)に関する不等式\( x^2-2x+2 > 0\)を解け。

はなこ

…この不等式の解は「すべての実数」よ。

たろぅ

あー…きたきた。もうアレだ、わけわかんねぇよ…。なんだよ、「=0」の解はないくせに解は「すべての実数」って。

ということで、二次不等式で一番「？」となるのがこのパターンですね。

ですが、これも二次不等式の解き方まとめの

グラフを利用する。
不等式の意味を押さえておく。

の２つができていれば大丈夫です。

この押さえ方が適当で『とりあえず「=0」の解を求めればいいんでしょ？』という考え方だとわけがわからなくなります。

せんせ

でも、この押さえがしっかりしていればすぐに理解できますよ！特に②の不等式の意味を押さえておくことが重要です。

まずはグラフをイメージして、不等式の意味を押さえます。

今回の例題では\( x^2-2x+2 > 0\)、つまり、左辺のグラフを考えたときに「グラフの\(y>0\)となる\(x\)の範囲は？」という意味になります。

そこで、\(x^2-2x+2 =0\)という方程式を解いてみますが、残念ながらこの方程式には実数解がありません。ですが、

たろぅ

じゃあ「解なし」だ！

と決めつけるのは早とちりですね…。ここで、『「=0」としたときの解がない』ということと『グラフの\(y>0\)となる\(x\)の範囲は？』の意味を考えてみます。

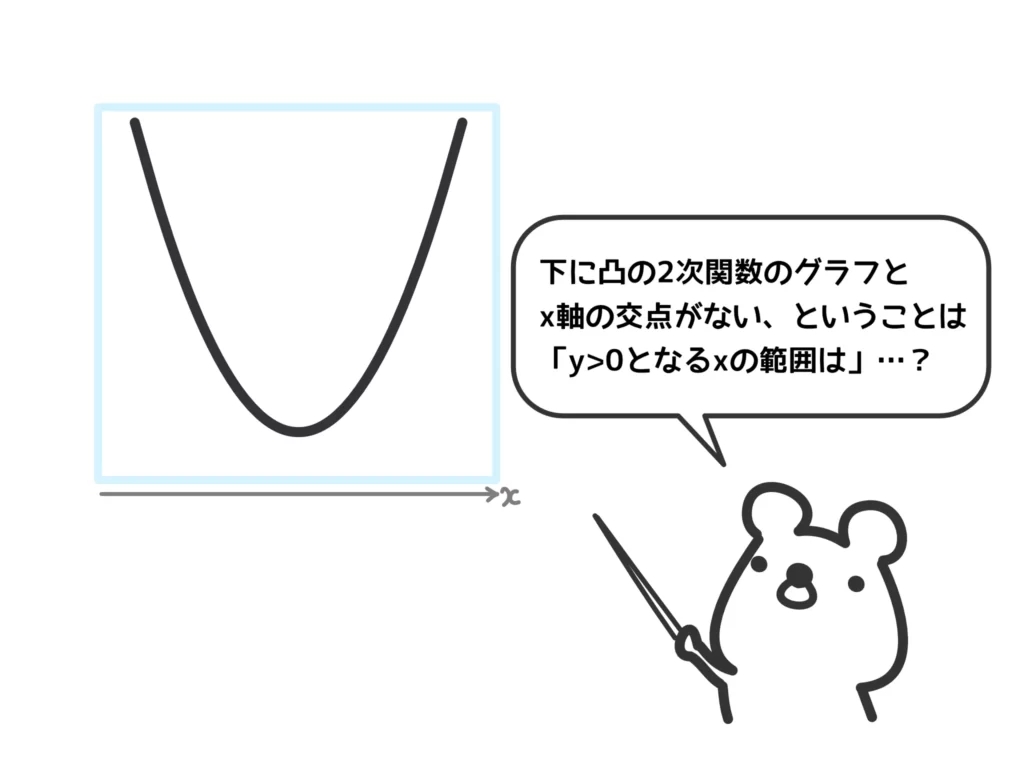
上図のように、『「=0」としたときの解がない』ということはグラフと\(x\)軸が交点を持たない、ということです。

つまり、不等式『グラフの\(y>0\)となる\(x\)の範囲は？』の答えとしては、

「どの\(x\)でも\(y>0\)でしょ？だってグラフが\(x\)軸より上に来てるんだから」

ということになり、「すべての実数」となります。

せんせ

『「=0」が解をもたなかったこと』と『不等式の意味』をグラフを通して読み取る必要があります。

たろぅ

なるほど…。まずグラフと不等式の意味を考えるのか…。

同じようなパターンで、

例4．\(x\)に関する不等式\( x^2-2x+2 < 0\)を解け。

という問題なら、「グラフの\(y<0\)となる\(x\)の範囲は？」という意味になるので、「=0」の解をもたない、という状況は先程と同じですが答えは「解なし」になります。

さっきの例とは逆で、\(x\)がどのような値でもグラフが\(y<0\)となることはないからです。

せんせ

これが重解をもつ（＝グラフが\(x\)軸に接する）ときと、「不等号に＝が入るかどうか？」などがカラむと、答えはより複雑になります。グラフをイメージして、じっくりと不等式の意味を考えましょう。

例5．(1) \(x\)に関する不等式\( (x-2)^2 > 0\)を解け。
　(2) \(x\)に関する不等式\( (x-2)^2 \geq 0\)を解け。
　(3) \(x\)に関する不等式\( (x-2)^2 < 0\)を解け。
　(4) \(x\)に関する不等式\( (x-2)^2 \leq 0\)を解け。

(1)~(4)のグラフと不等式の意味を図にすると次のようになります。

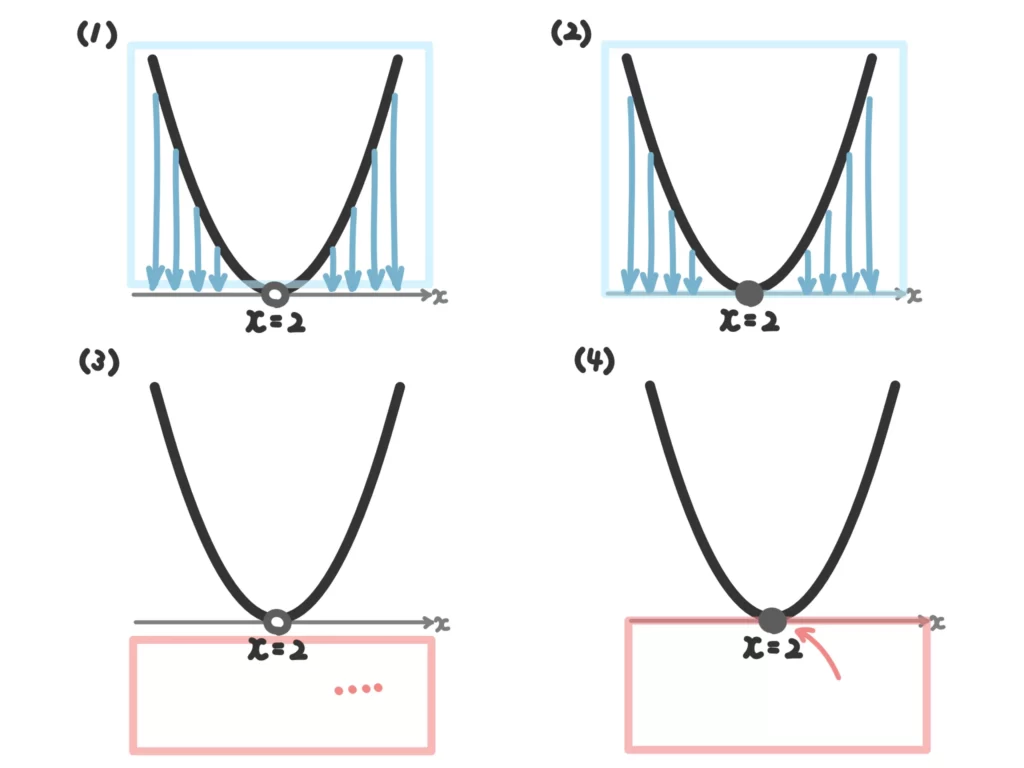
よって、
(1) \(x=2\)以外のすべての実数。
(2) すべての実数。
(3) 解なし。
(4) \(x=2\)。

x軸と交点をもたないときの二次不等式のおすすめの解き方

このタイプは判別式とグラフをかく解答も多いですが、解答としては面倒なのであまりオススメできません。

個人的にオススメするのは「平方完成してしまう」書き方です。

せんせ

このあと解説しますが、答えのパターンを調べるために平方完成をした方がいいんです。なので、解答も平方完成する方が楽ですし、説得力があります。例3の解答を作ってみましょう。

例3．\(x\)に関する不等式\( x^2-2x+2 > 0\)を解け。

（解答）

\( x^2-2x+2 > 0\)より、

\((x-1)^2+1>0\)

これを満たす\(x\)はすべての実数…（答）

せんせ

平方完成は\( (\quad)^2 + k\)の形を作るので、この形を見せるだけで「0より大きいよね」という説得力が出てきます。

二次不等式の解のパターンと見分け方

よく

たろぅ

二次不等式の解のパターンと調べ方を教えて下さい！

という質問を受けます。

ですが、二次不等式の答えは「グラフのイメージと不等式の意味」を押さえてその都度判断するしかありません。

せんせ

その中でも、判断基準となるポイントを押さえていきましょう。

まず、最初の判断としては、

①　グラフと\(x\)軸が「交わらない」「接する」「２つの交点をもつ」のいずれになるか？

を判断することです。

この判断として、判別式とグラフを使う解答がありますが、正直微妙かな…と思います。

判別式はあくまで二次方程式の実数解がいくつか？という判断しかできないので、解答としてはグラフとの合せ技で記述するしかないからです。

ではどうするか？というと、オススメは平方完成をすることです。完全に平方完成の計算をしてしまわなくても、\(ax^2+bx+c \)の\(a\)、\(b\)、\(c\)の値を見て大体のアタリをつけます。

下に凸のグラフを平方完成するときには

\(ax^2+bx+c \)の\(c\)の部分が＋の値＆\(b\)の値に対して大きければ、平方完成をしたときグラフと\(x\)軸が交わらない可能性が高くなります。

②「交わらない」とき

この場合、あとは不等式の意味を押さえるだけです。「＜」か「＞」によって、「解なし」か「すべての実数」のいずれかになります。

③「接する」とき

グラフが接する、つまり\( (\quad)^2\)の形になるときが一番複雑です。グラフをかいて、丁寧に解を求めてください。不等号に＝が入るかどうかによっても答えが変わってきます。

④「２点で交わる」とき

この場合、あとは「=0」の答えを求めて、それを基準に\(x\)の範囲を出すだけです。

せんせ

ざっくりと頭の中で平方完成して、グラフが\(x\)と交わるかどうか判断する…これができれば二次不等式はOKです。

実際に例1、例2、例3が\(x\)軸と交わるか判断してみる

例1．\(x\)に関する不等式\( x^2-x-2 > 0\)を解け。

例2．\(x\)に関する不等式\( -x^2+2x+4 \geq 0\)を解け。

例3．\(x\)に関する不等式\( x^2-2x+2 > 0\)を解け。

平方完成は大まかに言うと、

\(x^2\)の係数でくくる。
（\(x\)の係数の半分）の２乗（に①の係数を掛けたもの）を引く。

という操作です。②の段階で大体の様子がわかります。

例1については、\(x^2\)の係数でくくる必要はないので、単純に（\(x\)の係数\(-1\)の半分）の２乗を引きます。このとき、定数項の\(-2\)もあるので、明らかに頂点の\(y\)座標はー（マイナス）になるので\(x\)軸と２点で交わることがわかります。

例2については、ー（マイナス）を払った\( x^2-2x-4 \leq 0\)で判断しますが、これも同様に考えたら\(y\)座標はー（マイナス）になるのがわかると思います。

例3については、\(x^2\)の係数でくくる必要はないので、単純に（\(x\)の係数\(-2\)の半分）＝\(-1\)の２乗を引きます。ですが、定数項の\(+2\)があるので、頂点の\(y\)座標は＋になります。よって、\(x\)軸とは交わらないことがわかります。

せんせ

こんな感じでざっくりと平方完成をイメージして、頂点の\(y\)座標が＋になるかー（マイナス）になるかを判断してください。

二次不等式の問題

せんせ

それでは、いくつか問題を出してみましょう。

練習問題2-3【No.9】

問．次の二次不等式を解け。
(1) \(x^2+4x-12 \geq 0 \)
(2) \(2x^2+\sqrt{2}x -2 < 0\)
(3) \(x^2-4\sqrt{3}x + 5\sqrt{6} < 0\)

答え

(1) \(x \leq -6, 2 \leq x\)
(2) \(\displaystyle -\sqrt{2} < x < \frac{\sqrt{2}}{2}\)
(3) 解なし。

練習問題2-4【No.10】

問．次の式の解が与えられる結果となるように、\(\fbox{1}\)に数字、\(\fbox{2}\)に等号、不等号を埋めよ。

\( ( x – 3 ) (x – \fbox{1}) \fbox{2}0\)

(1) \( 3 \leq x \leq 5\)
(2) すべての実数。
(3) \( x = 3 \)

答え

(1) \(\fbox{1} \rightarrow 5,\fbox{2} \rightarrow \leq\)
(2) \(\fbox{1} \rightarrow 3,\fbox{2} \rightarrow \geq\)
(3) \(\fbox{1} \rightarrow 3,\fbox{2} \rightarrow =\)
　または\(\fbox{1} \rightarrow 3,\fbox{2} \rightarrow \leq\)