PR
相関係数の求め方や範囲が-1≦r≦1になる理由って?

相関係数…ご存知でしょうか?
高校数学で言えば、数学Iの「データの分析」で出てくるのですが、相関係数は、2つの変量の間にどのような関係があるか?を数値化したものです。
ただ、教科書でも相関係数の基本的な部分は押さえますが、実はあまり詳しく述べられることがありません。
ここでは、相関係数の基本的な性質から、なぜそのような値を考えたりそのような範囲になるのか?について解説していきます。
相関係数とは?
いきなりですが、「データの相関」というものを実感してもらうために、データの例をあげておきます。
例.以下のデータはAさん〜Jさんまでの、国語と英語、国語と数学、国語と理科のテストの得点を並べたものです。
| A | B | C | D | E | F | G | H | I | J | |
|---|---|---|---|---|---|---|---|---|---|---|
| 国語 | 50 | 70 | 40 | 90 | 65 | 30 | 30 | 80 | 85 | 60 |
| 英語 | 55 | 60 | 40 | 95 | 75 | 20 | 45 | 65 | 90 | 60 |
| A | B | C | D | E | F | G | H | I | J | |
|---|---|---|---|---|---|---|---|---|---|---|
| 国語 | 50 | 70 | 40 | 90 | 65 | 30 | 30 | 80 | 85 | 60 |
| 数学 | 80 | 65 | 50 | 40 | 90 | 55 | 30 | 40 | 90 | 75 |
| A | B | C | D | E | F | G | H | I | J | |
|---|---|---|---|---|---|---|---|---|---|---|
| 国語 | 50 | 70 | 40 | 90 | 65 | 30 | 30 | 80 | 85 | 60 |
| 理科 | 45 | 40 | 75 | 35 | 25 | 80 | 75 | 35 | 30 | 40 |
これらのデータの組み合わせを横軸、縦軸に平面状にプロットしたものを散布図、といいます。国語ー英語、国語ー数学、国語ー理科の散布図は次のようになります。
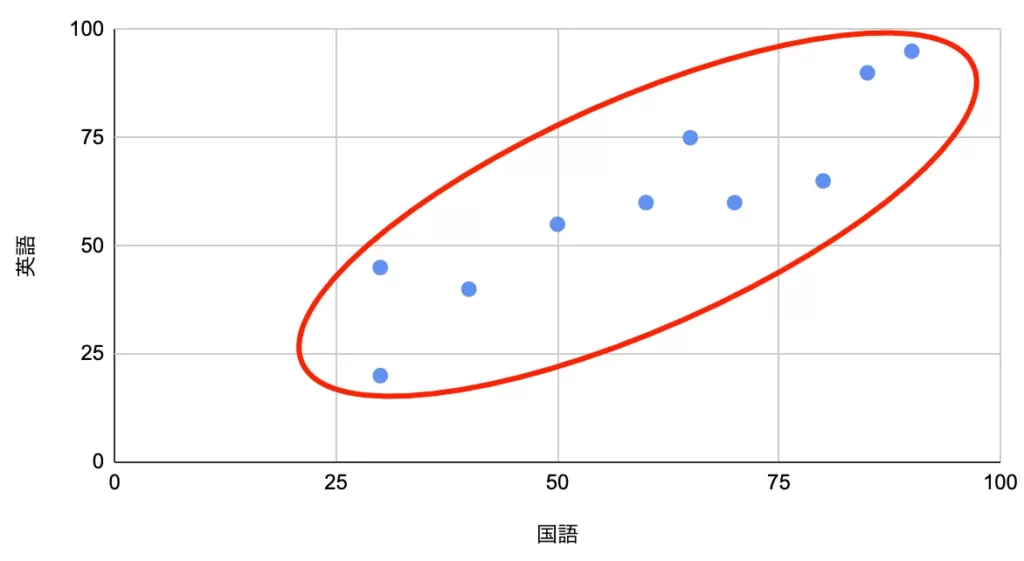
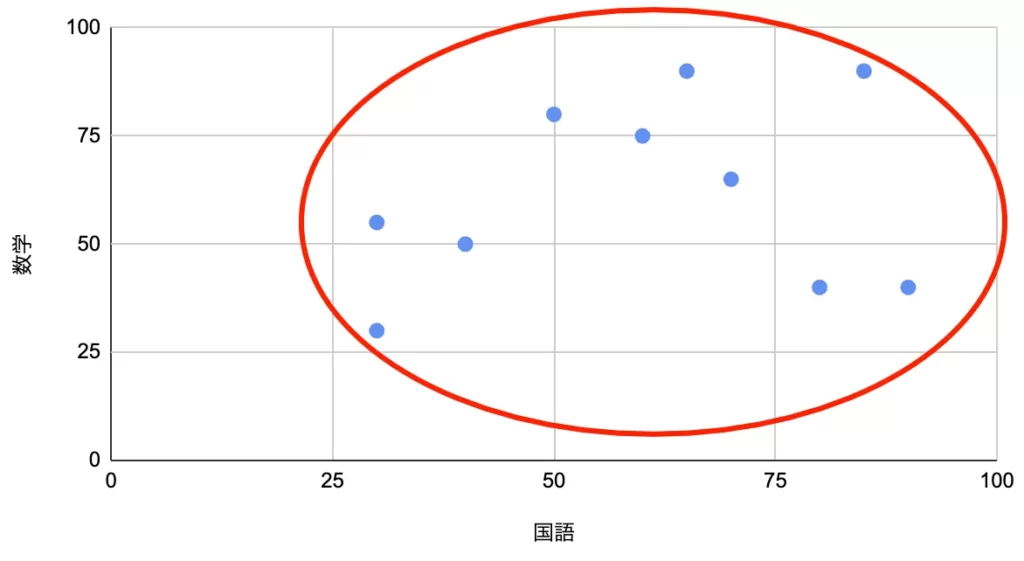
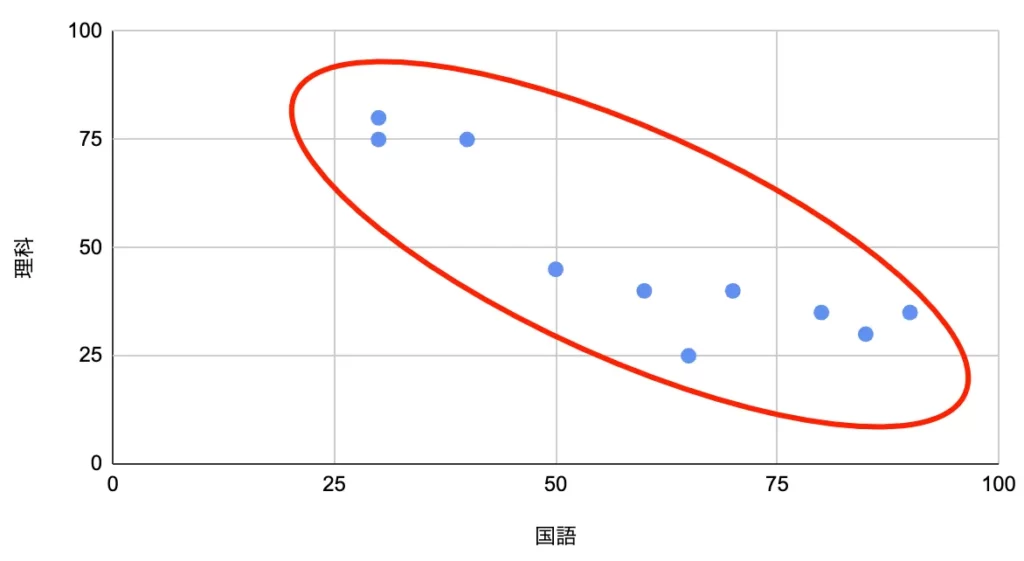
右肩上がりになるほど「正の相関がある」といいます。
右肩下がりになるほど「負の相関がある」といいます。
正の相関も負の相関もないときに「相関がない」といいます。
数学をモチーフにしたオシャレなオリジナルグッズも販売中です!おかげさまで好評頂いてます!
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ!
相関係数の求め方
相関係数は計算が結構大変ですが、求め方を載せておきます。
まずは共分散というものを求めます。
共分散
2つの変数の組\( x_i\)、\( y_i \)(\(i = 1 , 2 , \cdots , n\) )について、\( x_i\)、\( y_i \)の平均をそれぞれ\( \bar{x}\)、\( \bar{y} \)とすると、共分散\( s_{xy}\)は
$$\displaystyle s_{xy}= \frac{1}{n} \{ (x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y}) \}$$
で求めることができる。
共分散は、それぞれのデータ\((x_i-\bar{x})(y_i-\bar{y})\)において、右肩上がりのラインに近ければ+(プラス)、右肩下がりのラインに近ければー(マイナス)の値をとります。
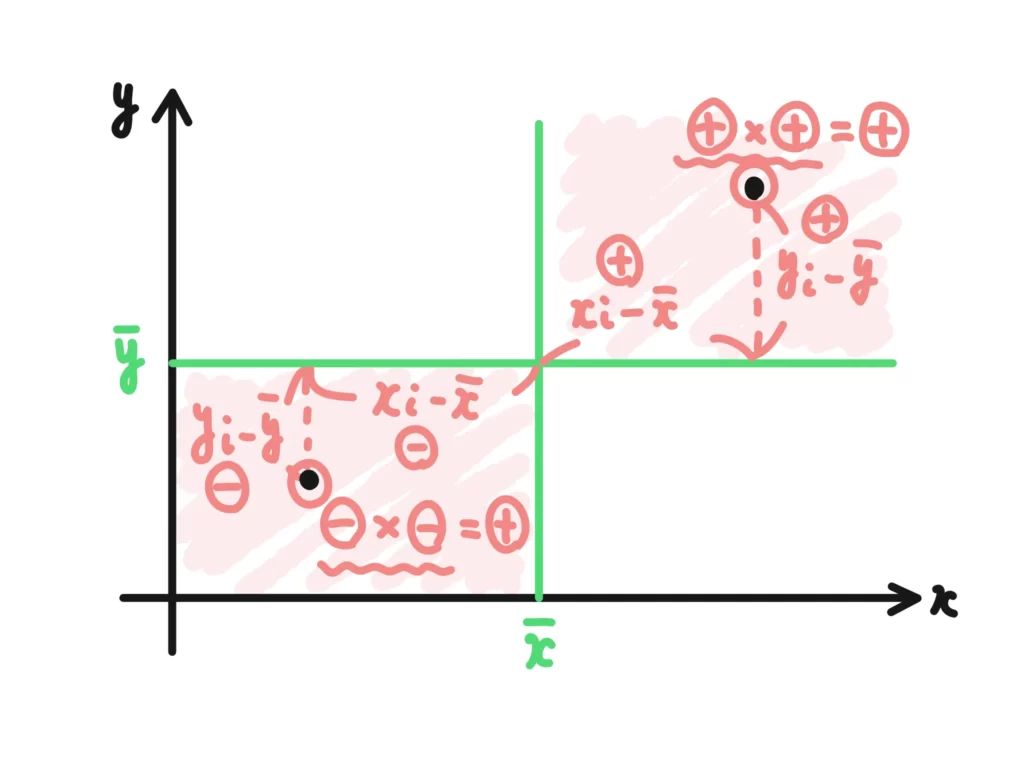
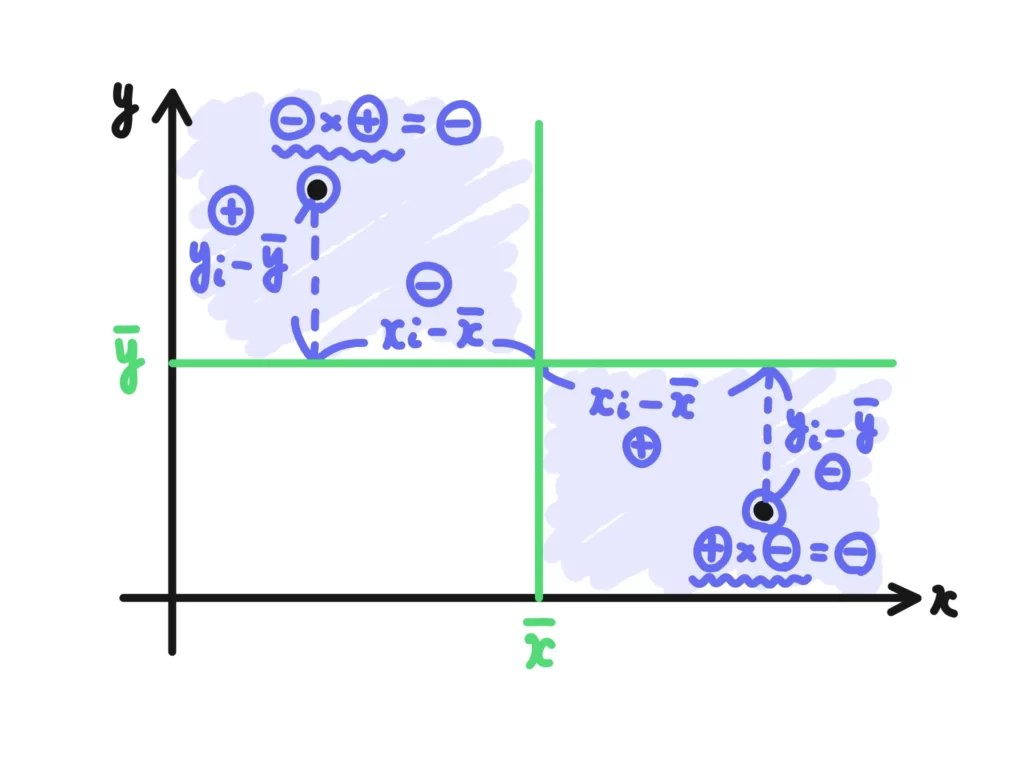
この共分散\( s_{xy}\)を使って、相関係数は次のように計算することができます。
相関係数
\( x_i\)、\( y_i \)の標準偏差\(s_x\)、\(s_y\)と共分散\( s_{xy}\)とすると、相関係数\(r\)は
\(\displaystyle r=\frac{ s_{xy}}{s_x s_y}\)
で求めることができる。
ちなみに標準偏差は\(\sqrt{分散}\)で求めることができます。具体的には、
$$ \displaystyle s_x=\sqrt{\frac{1}{n} \{ (x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2 \}} $$
で計算します。ですので、相関係数は1つ1つのデータからガチンコで計算すると、実質次のような計算になります。
相関係数の具体的な計算方法
\(\displaystyle r=\frac{ s_{xy}}{s_x s_y}\)
$$\displaystyle =\frac{\frac{1}{n} \{ (x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y}) \} }{ \sqrt{ \frac{1}{n} \{ (x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2 \} } \sqrt{\frac{1}{n} \{ (y_1-\bar{y})^2+(y_2-\bar{y})^2+\cdots+(y_n-\bar{y})^2 \}}}$$
$$\displaystyle =\frac{ (x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y}) }{\sqrt{ (x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2 } \sqrt{ (y_1-\bar{y})^2+(y_2-\bar{y})^2+\cdots+(y_n-\bar{y})^2 }}$$
 たろぅ
たろぅ…せんせい!僕はもう相関係数を求めたくありません!



うん、そうですね、わかりますよ。



え?じゃあ計算しなくていいですか?



いや、まぁ面倒ですけど、計算してください。



なぜじゃあ…。
相関係数を手で計算するのは大変です。表で上手くまとめたり、散布図を使ったりして計算していきましょう。
ちなみに、共「分散」と標準偏差=\(\sqrt{(分散)}\)を使うので、よく、
\(\displaystyle r = \frac{(共分散)}{(xの分散)(yの分散)} \)
と間違えやすいです。
分子の(共分散)→\(x\)、\(y\)の二次式、分母の標準偏差×標準偏差→\(\sqrt{(xの二次式)}\)×\(\sqrt{(yの二次式)}\)→実質の次数として\(x\)、\(y\)の二次式
という、分母、分子の変数の次数が揃っているか確認するといいです。
共分散の基本的な性質
① 共分散\(r\)は\(-1 \leq r \leq 1 \)の範囲になります。
なぜそうなるのか?は後で説明します。
② 共分散は\(1\)に近ければ「正の相関」、\(-1\)に近ければ「負の相関」、\(0\)に近ければ「相関なし」と言えます。



もう一度最初の散布図を見てみましょう。






確かに、共分散と散布図には上記のような結びつきが見られますね。
よく相関係数の範囲を\(0 \leq r \leq 1\)なんかと間違える人がいますが、「正の相関」「負の相関」という言葉のイメージと合わせると覚えやすいです。
ちなみに、相関の目安ですが、
- \(r\)が0.7〜1(-0.7〜-1):強い相関あり
- \(r\)が0.4〜0.7(-0.4〜-0.7):やや相関あり
- \(r\)が0.2〜0.4(-0.2〜-0.4):弱い相関あり
- \(r\)が0〜0.2(0〜-0.2):ほとんど相関なし
となります。
相関係数の範囲はなぜ「-1≦r≦1」なのか?証明!
これはあまり触れられることが多くないのですが、面白いので証明しておきます。
こちらで説明している「コーシーシュワルツの不等式」を使いますので、そちらもあわせて確認してみてください!


(証明)
コーシーシュワルツの不等式から
$$ (a_1^2+a_2^2+ \cdots +a_n^2)(b_1^2+b_2^2 +\cdots +b_n^2) \geq (a_1 b_1 + a_2 b_2+ \cdots + a_n b_n)^2 $$が成り立つ。
\( (a_1^2+a_2^2+ \cdots +a_n^2)(b_1^2+b_2^2 +\cdots +b_n^2) \geq 0 \)なので、両辺を\((a_1^2+a_2^2+ \cdots +a_n^2)(b_1^2+b_2^2 +\cdots +b_n^2) \)で割って、
$$\displaystyle 1 \geq \frac{(a_1 b_1 + a_2 b_2+ \cdots + a_n b_n)^2}{(a_1^2+a_2^2+ \cdots +a_n^2)(b_1^2+b_2^2 +\cdots +b_n^2)} $$
つまり、
$$\displaystyle -1 \leq \frac{a_1 b_1 + a_2 b_2+ \cdots + a_n b_n}{\sqrt{a_1^2+a_2^2+ \cdots +a_n^2} \sqrt{b_1^2+b_2^2 +\cdots +b_n^2}} \leq 1 $$
(↑\(x^2 \leq 1\)を解くと\(-1 \leq x \leq 1\)となることを利用した)
ここで、
\(a_1 \rightarrow (x_1-\bar{x})\)、\(a_2 \rightarrow (x_2-\bar{x})\)、…、\(a_n \rightarrow (x_n-\bar{x})\)、
\(b_1 \rightarrow (y_1-\bar{y})\)、\(b_2 \rightarrow (y_2-\bar{y})\)、…、\(b_n \rightarrow (y_n-\bar{y})\)
に置き換えると、
$$\displaystyle -1 \leq \frac{ (x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y}) }{\sqrt{ (x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2 } \sqrt{ (y_1-\bar{y})^2+(y_2-\bar{y})^2+\cdots+(y_n-\bar{y})^2 }} \leq 1$$
よって上記の「相関係数の具体的な計算方法」の式から
\( -1 \leq r \leq 1 \)が成り立つ(終)



コーシーシュワルツの不等式を使えば、かなりエレガントに証明できるので面白いですね。
まとめ
相関係数の求め方や基本事項と、なぜ範囲が「-1≦r≦1」なのか?の証明をしました。
高校のテストなど、実用面でいえば、とりあえず「間違えずに計算」できて「相関係数の範囲と相関関係が読み取れる」くらいでいいかな、と思います。
個人的には「相関係数の範囲がなぜ-1≦r≦1になるのか?」が面白いと思うので興味がある人はぜひ確認してください!










