ベクトルの引き算とは？超重要な使い方の解説！

2023年10月22日

ベクトルは便利で重要な考え方ですが、苦手な人が多い分野でもあります。

原因は「イメージ」と「その場での思考」が重要だからです。

たろぅ

その状況に応じた対応って苦手…。

ですが、その分覚えることも少ないですし、基本的なイメージをしっかりと掴むことができればあとはちょっと練習するだけでベクトルの理解はかなり深まります。

せんせ

要は最初の本質部分が大事！
「ベクトルは感覚だ！」

この記事では、ベクトルの引き算とその重要な使い方について説明していきます。

せんせ

そこまでボリュームはないのでサクッといきましょう！

ベクトルの引き算とは？

ベクトルの引き算は簡単にいうと、

「逆ベクトルを足しましょう」

というお話です。

せんせ

ベクトルの足し算については別の記事にしていますので、そちらも見ていただけたら、と思います。

ベクトルは「大きさ」と「向き」を持ちます。

そこで、同じ大きさで逆向きのベクトルを逆ベクトルといい、「ー（マイナス）」をつけて表そう、という話です。

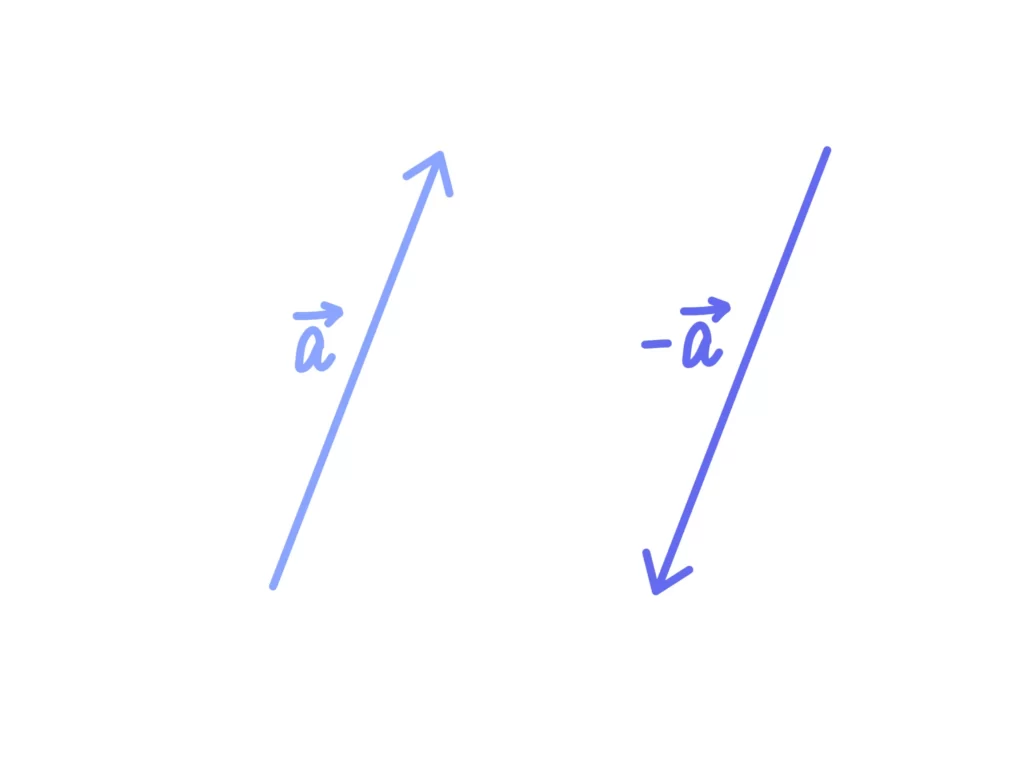
逆ベクトル

あるベクトル\(\overrightarrow{a}\)に対して大きさが同じで逆向きのベクトルを逆ベクトルといい、\(-\overrightarrow{a}\)とかく。

ということで、ベクトルの引き算とは逆ベクトルを加えることで表現していきます。

ベクトルの引き算

\(\overrightarrow{a}-\overrightarrow{b} = \overrightarrow{a} + (- \overrightarrow{b})\)

と定める。

たろぅ

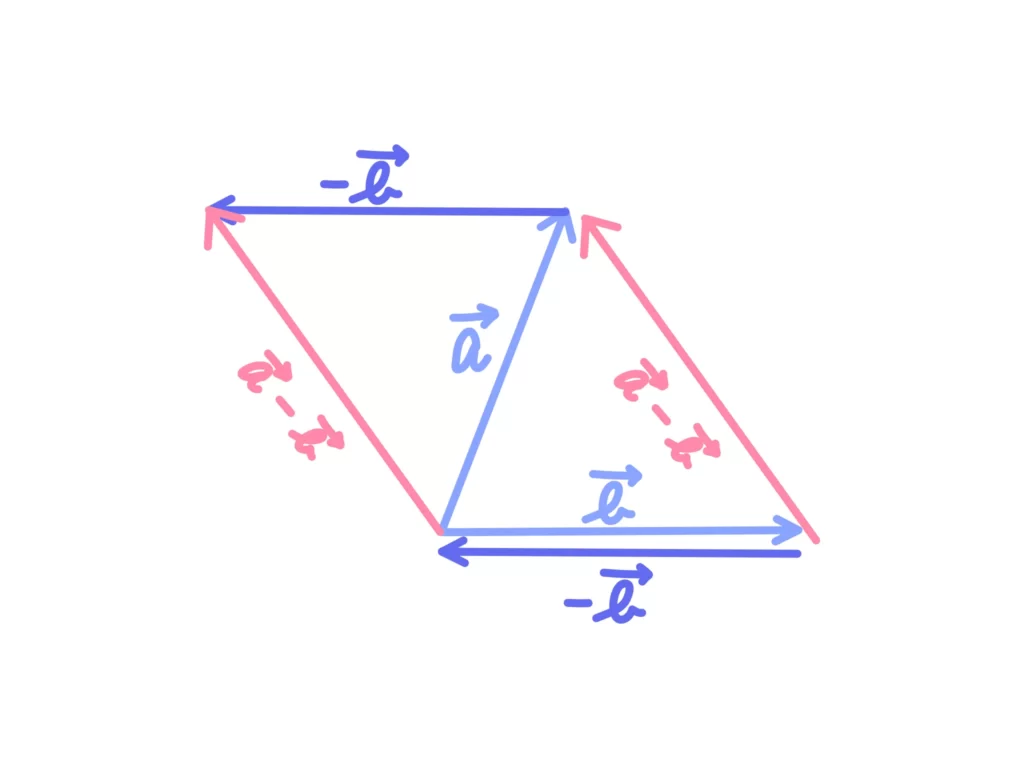
んー…言ってることはわかるけど、なんとなく図の意味がわかりにくいんだけど…。

となるかもしれません。

でも大丈夫。このベクトルの引き算、ベクトルの足し算と違ってあまり図形的な意味が重要になることはないです。

せんせ

その代わり、引き算は次で説明する超重要なベクトルの変形（式変形）があります！ベクトルの引き算では、これだけは絶対に押さえておいてください！

結論からいうと、ベクトルの引き算は「始点を揃える」ときによく使います。

ベクトルの引き算を使って始点を揃える

\(\overrightarrow{AB} = \overrightarrow{OB}-\overrightarrow{OA}\)

どんなベクトルでも、任意の始点のからのベクトルと、その差を使って表すことができます。

せんせ

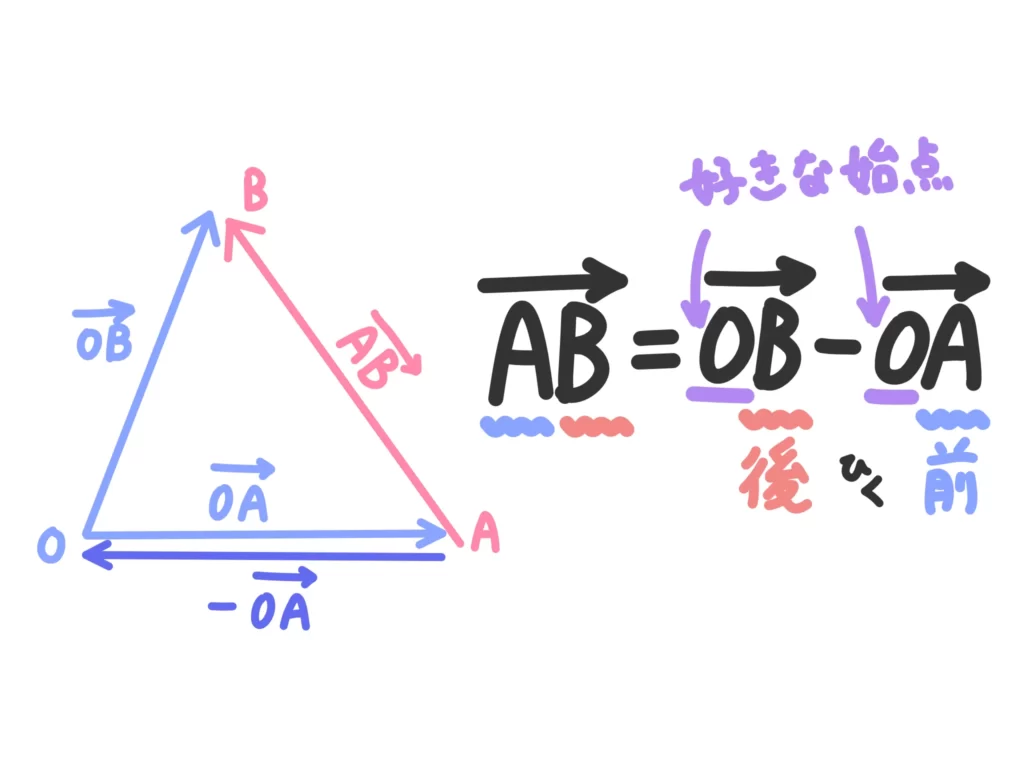
ぶっちゃけ図形的な意味はどうでもいいです。
機械的に任意の始点に揃えることができる、というところがポイントです。

このあと、特にベクトルの実践的な問題になってくると、この「始点を揃える」という操作が機械的にできないと上手く解けません。

せんせ

問題を解く際に「最初どうすればいいか分からない…」となったら、「とりあえず、問題で設定している始点に揃える」という操作が有効だったりします。覚えておいてソンはないです。

ベクトルの引き算についての解説でした。

引き算自体は逆ベクトルを足せばいい、という話ですが、引き算を使った「始点を揃える」作業は超重要ですので押さえておいてください。