2025共通テスト「数学ⅡBC」徹底解説！【予備校の解説ではできない私見も】

この記事では2025年1月19日に行われた共通テスト「数学ⅡBC」の解説をしていきます！

共通テスト数学ⅡB．第1問【三角関数】

(1)(i)　\(\alpha = \beta\)とすると、\(\displaystyle \theta + \frac{\pi}{6} = 2\theta \)。
これを解いて\(\displaystyle \theta = \frac{\pi}{6} \)。（答）
このとき、\(\displaystyle \sin{\Big( \theta + \frac{\pi}{6} \Big) } = \sin{2\theta} = \frac{\sqrt{3}}{2}\)。（答）

(ii) 単位円上の点と原点を結んだ線分と\(x\)軸正の方向と成す角のサインの値は、単位円上の点の\(y\)座標と等しいので「点Pの\(y\)座標と点Qの\(y\)座標が等しいときサインの値は等しい」。（答）

(iii)

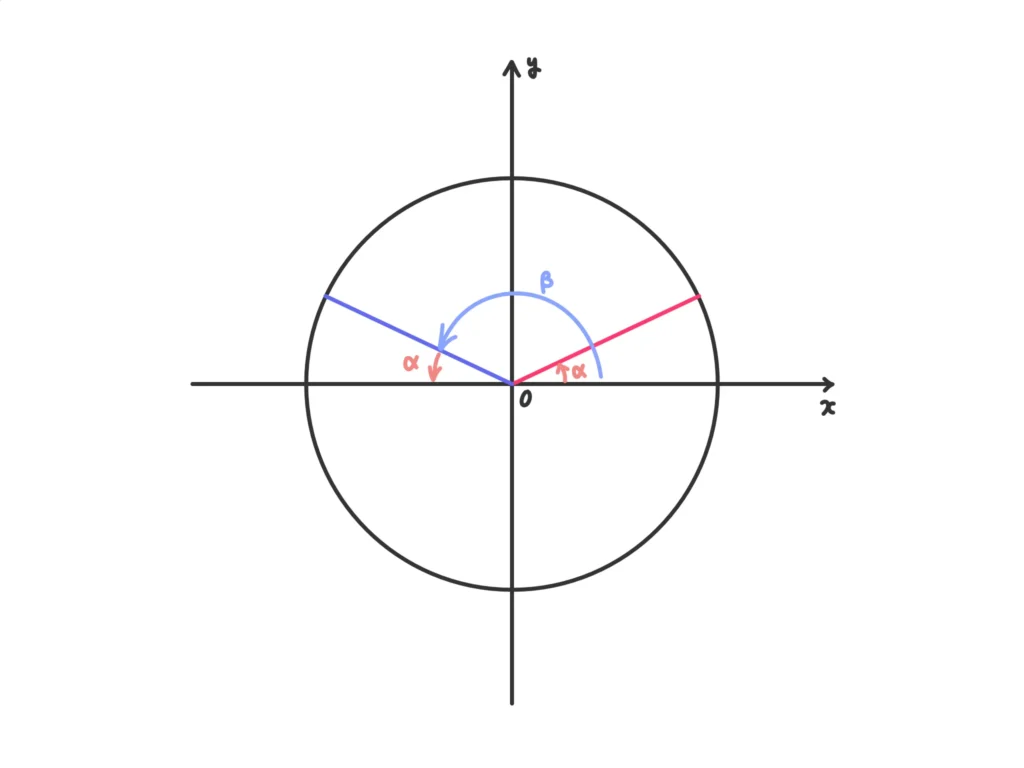
\( \alpha + \beta = \pi \)。（答）
\(\displaystyle \theta + \frac{\pi}{6} + 2\theta = \pi \)となるので、\(\displaystyle \theta = \frac{5}{18}\pi \)。（答）

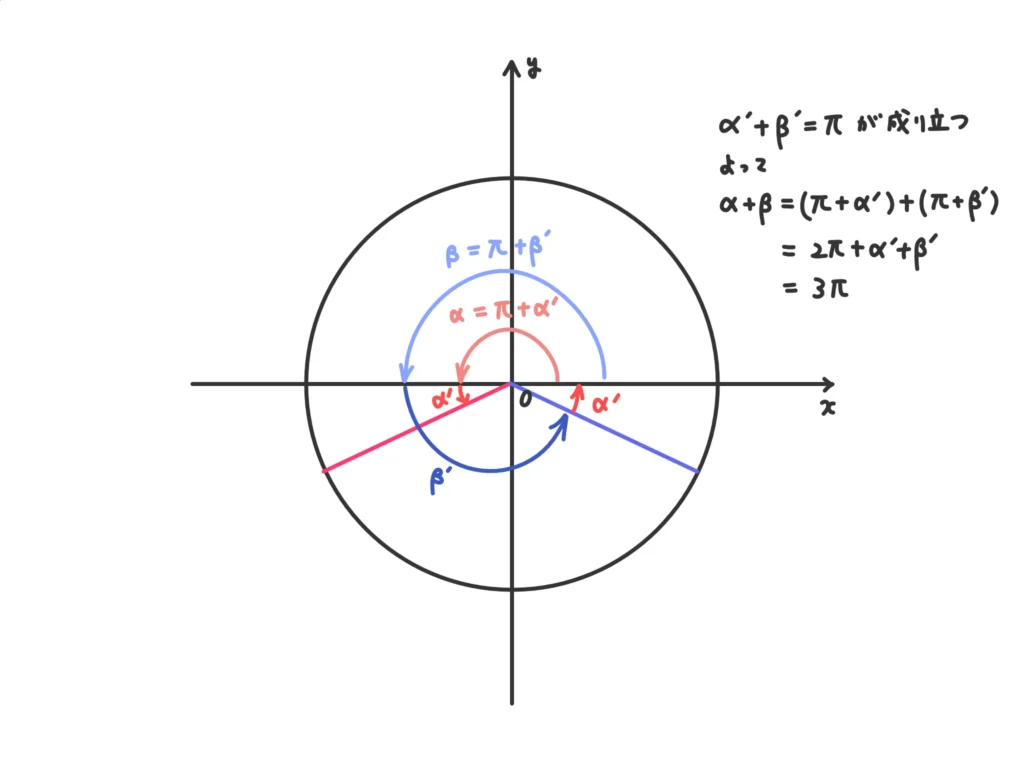
\( \alpha + \beta = 3\pi \)。（答）
\(\displaystyle \theta + \frac{\pi}{6} + 2\theta = 3\pi \)となるので、\(\displaystyle \theta = \frac{17}{18}\pi \)。（答）

(2)

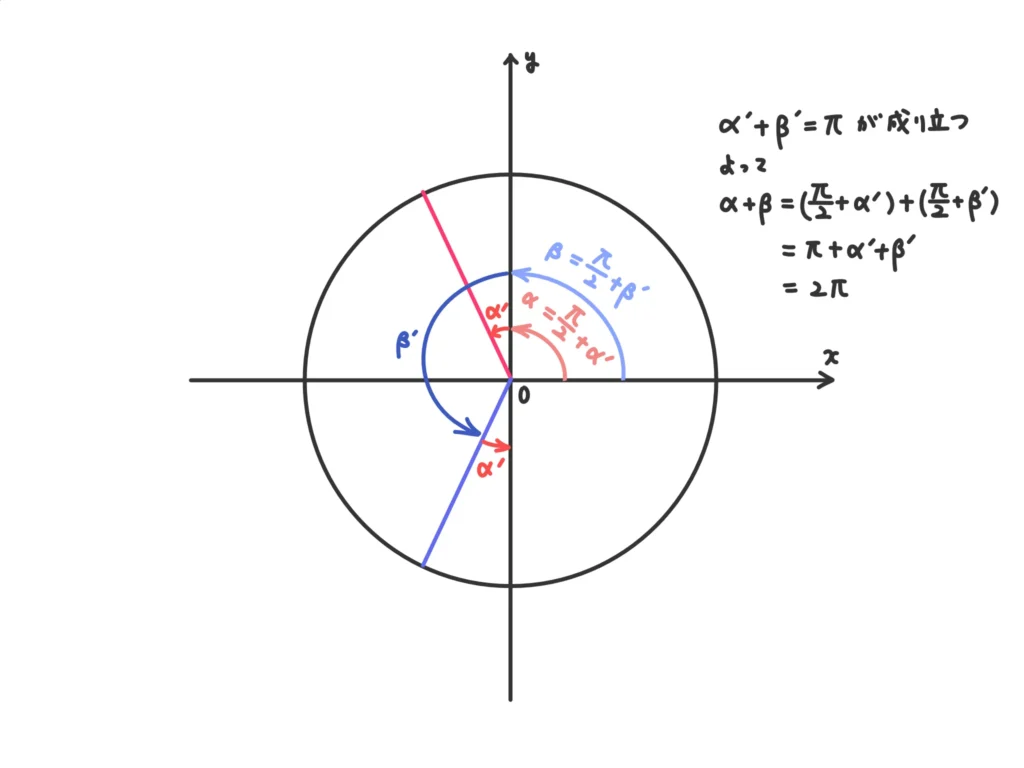
\(\displaystyle \cos{\Big( \theta + \frac{\pi}{6} \Big) } = \cos{2\theta}\)。単位円上の点の\(x\)座標が等しければよい。

\(\displaystyle 0 \leq \theta < \frac{\pi}{2}\)のとき\(\displaystyle 0 \leq 2\theta < \pi\)なので、\( \alpha = \beta \)となるパターンしかない。
このとき、\(\displaystyle \theta = \frac{\pi}{6} \)。（答）

\(\displaystyle \frac{\pi}{2} \leq \theta < \pi \)のとき\(\displaystyle \pi \leq 2\theta < 2\pi\)なので、\(\alpha + \beta = 2\pi\)となればよい。
\(\displaystyle \theta + \frac{\pi}{6} + 2\theta = 2\pi \)を解いて、\(\displaystyle \theta = \frac{11}{18}\pi \)。（答）

共通テスト数学ⅡB．第2問【指数関数・対数関数】

(1)　「１日ごとに一定の倍率で増える」という設定なので、\(r^3 = 1.32\)。（答）
常用対数表を使うと　\( \log_{10}{1.32} = 0.1206 \)。（答）
\(r^3 = 1.32\)の両辺常用対数をとって、
\( \log_{10}{r^3} = \log_{10}{1.32}\)
\( 3 \log_{10}{r} = 0.1206\)。よって、\( \log_{10}{r} = 0.0402\)。（答）

(2)　「最初\(a\)％、１日に増える倍率\(r\)（(1)で求めた値）、１４日後に６０％」となればいいので、
\( a \times r^{14} = 60\)。（答）
両辺常用対数をとって、
\( \log_{10}{ ( a \times r^{14} ) } = \log_{10}{60} \)
\( \log_{10}{a}+ 14 \log_{10}{r^{14}} = \log_{10}{6}+\log_{10}{10} \)
\( \log_{10}{a}+ 14 \times 0.0402 = 0.7782 + 1 \)。これを解いて、\( \log_{10}{a}=1.2154\)。（答）

\( \log_{10}{a}=1.2154\)より、\(a = 10^{1.2154}=10^1 \times 10^{0.2154}\)なので
\(10^{0.2154}\)について調べる。
\(k=10^{0.2154}\)として、両辺常用対数をとって整理すると\( \log_{10}{k} = 0.2154\)。
常用対数表を使うと\(1.64 < k < 1.65\)となる。つまり、\(1.64 < 10^{0.2154} < 1.65\)の値だとわかる。
\(a = 10^1 \times 10^{0.2154}\)なので、\(16.4 < 10^1 \times 10^{0.2154} < 16.5\)。
よって、\(a\)以下で最大の整数は16。（答）

共通テスト数学ⅡB．第3問【微分・積分】

(1) \( F(x) = 2x^3 + 3x^2\)を微分して\(f(x) = 6x^2 + 6x \)。（答）
\(f(x)=6x(x+1)\)。\(f(x) = 0\)とすると\(x=-1,0\)

\begin{array}{|c|ccccc|}
\hline
x & \cdots & -1 & \cdots & 0 & \cdots \\
\hline
f(x) & + & 0 & – & 0 & + \\
\hline
F(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\
\hline
\end{array}

\(F(x)\)は\(x=-1\)で極大値をとる。（答）
（実際は増減表なんかかいてる暇ない…けど、このあとの問題のために、このくらいかいておいても損はないかも）

「\(f(x)\)は２次関数」「\(F(x)\)と\(G(x)\)の導関数が同じ\(f(x)\)」であることから\(F(x)\)と\(G(x)\)の違いは定数部分のみだとわかる。
よって、\(G(x) = 2x^3+3x^2 + C\)とおける。（答）
増減表の区切りとなる\(x\)、増減も\(F(x)\)と一緒なので（定数部分だけ違うので上下スライドのイメージ。極大値・極小値だけ変わる）、\(G(x)\)は\(x=0\)で極小値をとる。（答）
条件から、\(G(x)\)は\(x=-1\)で極大値0をとるので、\(G(-1)=0\)。\(2(-1)^3+3(-1)^2+C=0\)より、\(C=-1\)。（答）

(2)(i) \(F(x)\)は\(x=0\)で極小となるので、導関数\(f(x)\)について\(f(0) = 0\)。（答）
極小となるところでは導関数\(f(x)\)の符号は負（マイナス）から正（プラス）に変わる。（答）
同様に\(G(x)\)に関しても、\(x=k\)で極大となるので、導関数\(f(x)\)について\(f(k) = 0\)。（答）
極大となるところでは導関数\(f(x)\)の符号は正（プラス）から負（マイナス）に変わる。（答）

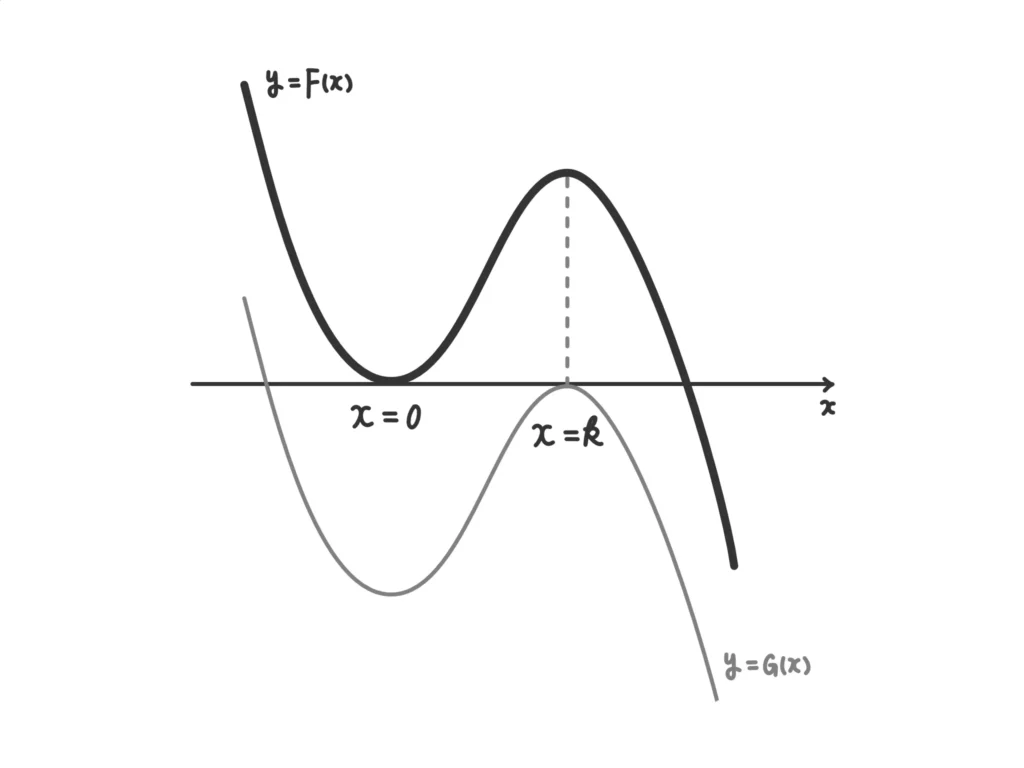
条件「\(F(x)\)は\(x=0\)で極小値をとる」「\(k>0\)」と、\(G(x)\)が極大になるところ（\(x=k\)）で\(F(x)\)も極大になる、ということでグラフの概形は次のようになる。（答）

(ii) \(F(0)=0\)なので
\(\displaystyle \int_0^x f(t) dt = \left[ F(t) \right]_0^x = F(x)-F(0)=F(x) \)。（答）
極大となるのは\(x=k\)のとき、つまり極大値は\(F(k)\)なので、上の積分の\(x=k\)とすればよい。極大値は\(\displaystyle \int_0^k f(t) dt \)。（答）
(i)\(F(x)\)のグラフの概形から\(f(x)\)は次のようなグラフになる。

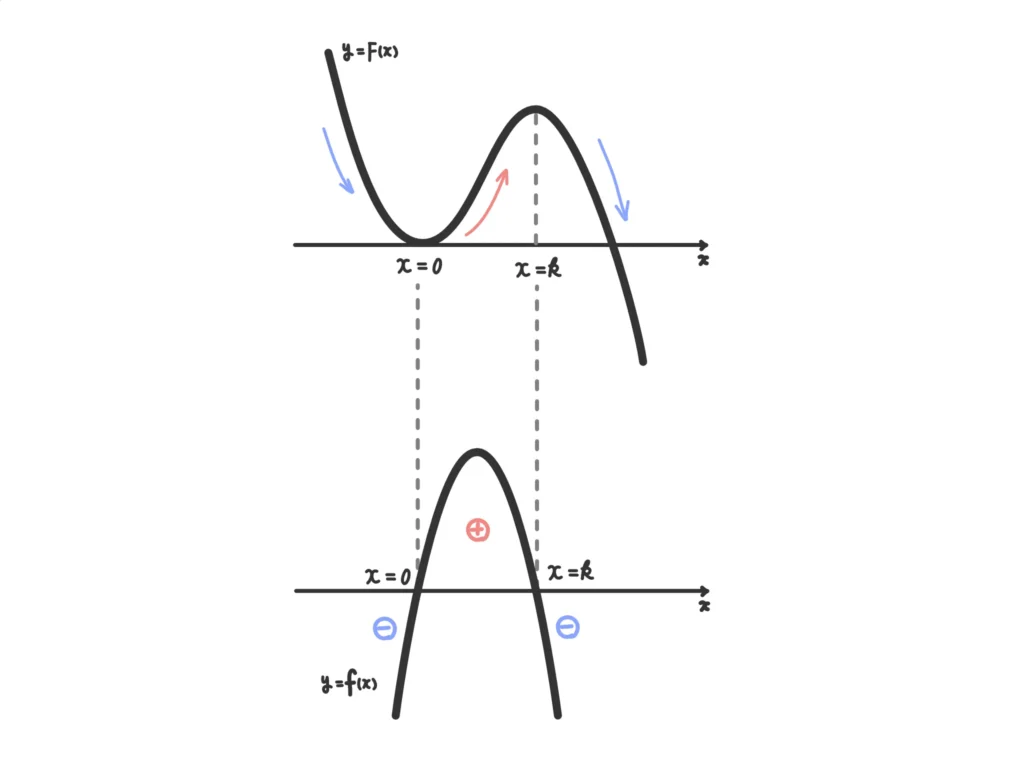
よって、極大値\(\displaystyle \int_0^k f(t) dt \)は\(y=f(x)\)と\(x\)軸で囲まれた図形の面積と等しい。（答）

また、\(F(x)\)と\(G(x)\)のグラフの概形は次のようになる。

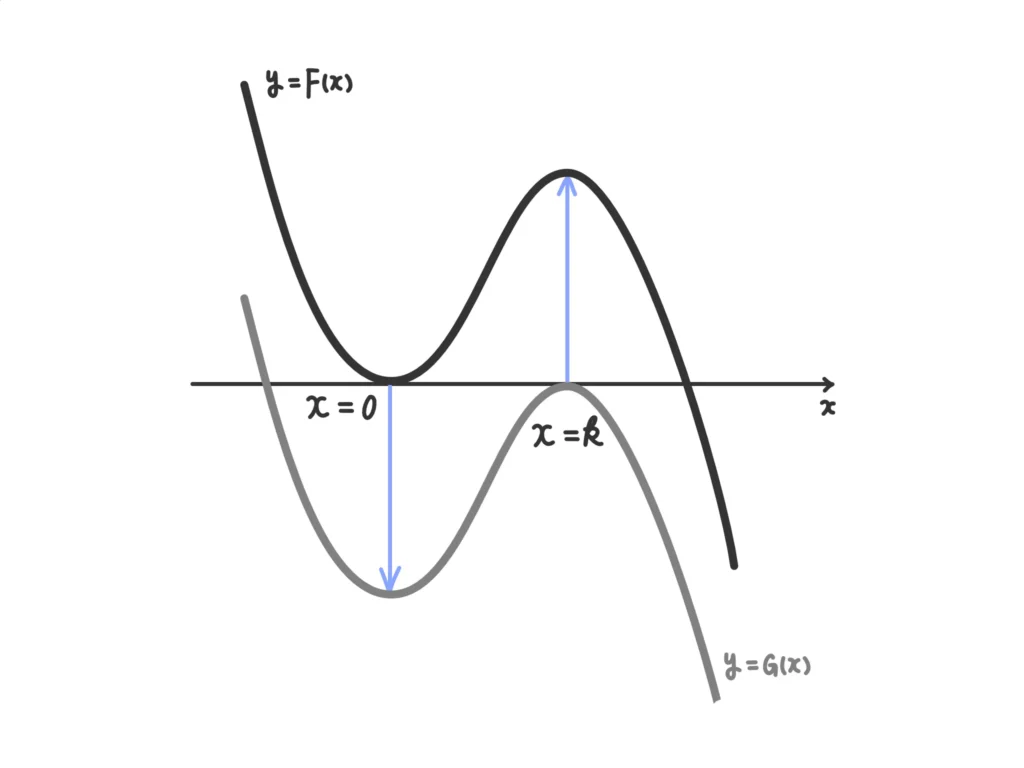
\(F(x)\)と\(G(x)\)のグラフは上下にスライドさせただけの関係なので、\(F(x)\)の極大値は\(G(x)\)の極小値を−１倍した値だとわかる。（答）

共通テスト数学ⅡB．第4問【数列】

(1)

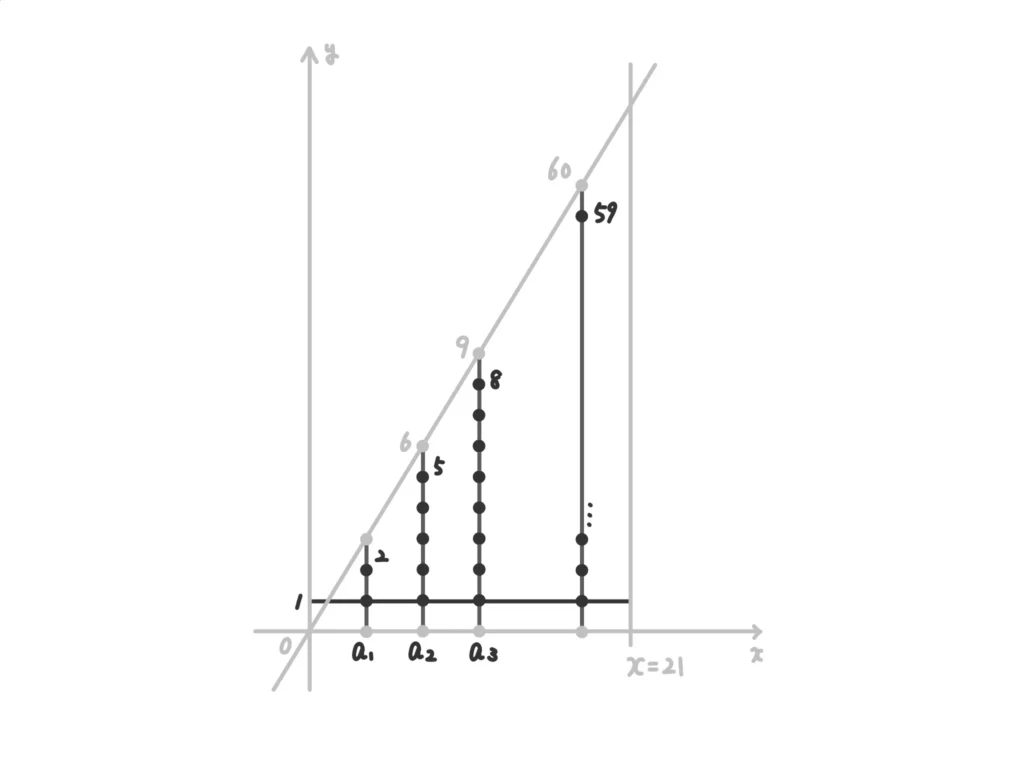
よって、\(a_2=5\)、\(a_3=8\)。数列\( \{ a_n \} \)は公差が3の等差数列。（答）

格子点の個数は項数20、初項2、末項59の等差数列の和。
よって、\(\displaystyle \frac{20}{2}(2+59) = 610\)。（答）

(2)

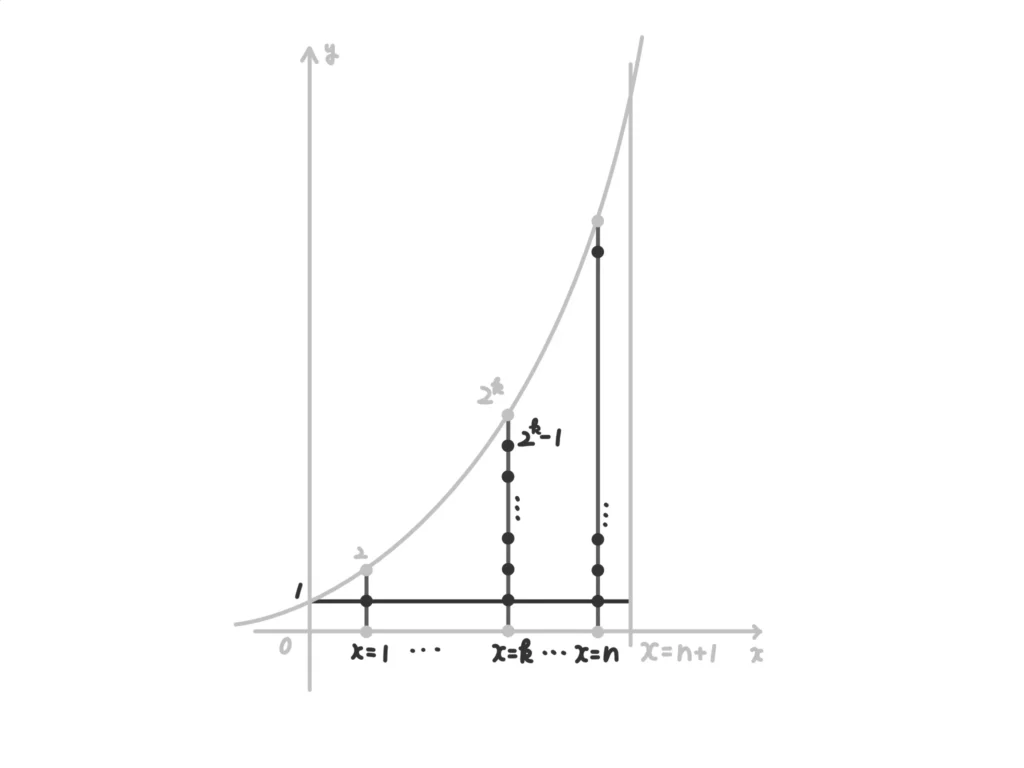
「\(x=k\)の境界上は必ず格子点がのる」ことと「境界上の格子点はカウントしない」ことに注意すると、\(x=k\)上の格子点でUの内部にあるものの個数は\(2^k-1\)個。（答）

\(x=n+1\)で囲まれているが、境界（\(x=n+1\)）上はカウントしないので、\(x=k\)上のU内部の格子点を\(k=1\)からその手前の\(x=n\)までの和で求めればよい。
\(\displaystyle \sum_{k=1}^{n}(2^k-1)= \frac{2(2^n-1)}{2-1}-n = 2^{n+1}-n-2\)。（答）

(3)

\(a>0\)、\(b^2-4ac<0\)より、次のような図になる。

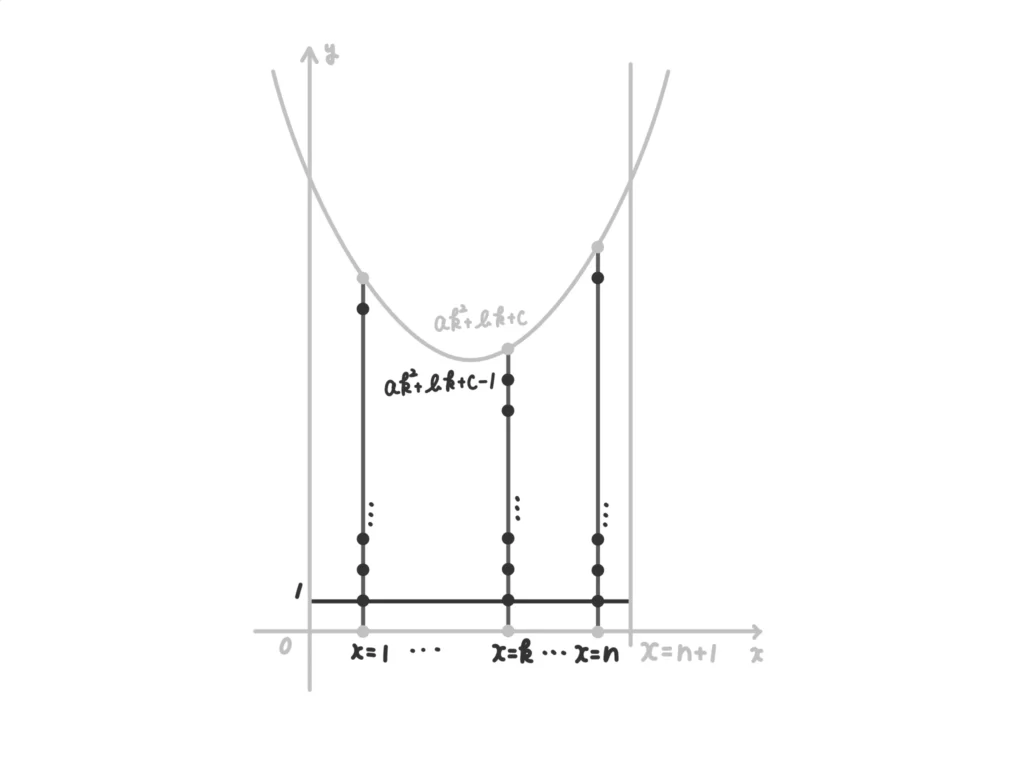
\(\displaystyle \sum_{k=1}^{n}(ak^2+bk+c-1)= a \frac{1}{6}n(n+1)(2n+1) + b \frac{1}{2}n(n+1) + (c-1)n \)
\(\displaystyle \quad = \frac{a}{3}n^3 + \Big( \frac{a}{2} + \frac{b}{2} \Big) n^2 + \Big( \frac{a}{6} + \frac{b}{2}+ c-1 \Big) n \)
よって、\(\displaystyle \frac{a}{3}n^3 + \Big( \frac{a}{2} + \frac{b}{2} \Big) n^2 + \Big( \frac{a}{6} + \frac{b}{2}+ c-1 \Big) n =n^3\)
これがすべての\(n\)について成り立つので、

\( \begin{cases}
\displaystyle \frac{a}{3} = 1 \\
\displaystyle \frac{a}{2} + \frac{b}{2} = 0 \\
\displaystyle \frac{a}{6} + \frac{b}{2}+ c-1 = 0
\end{cases} \)

\( \begin{cases}
\displaystyle a = 3 \\
\displaystyle b = -3 \\
\displaystyle c = 2
\end{cases} \)（答）

共通テスト数学ⅡB．第5問【統計的な推測】

(1) レモンの重さの確率変数\(X\)は正規分布\( N ( 110, 20^2 ) \)に従うので \(\displaystyle Z_1 = \frac{X-110}{20} \)とすると、\(Z_1\)は標準正規分布\( N ( 0, 1 ) \)に従う。
\(\displaystyle P(110 \leq X \leq 140) = P( \frac{110-110}{20} \leq Z_1 \leq \frac{140-110}{20} ) = P(0 \leq Z_1 \leq 1.5)\)
標準正規分布表から、0.4332。（答）

Lサイズのレモンの個数\(Y\)は二項分布\( B (20万, 0.4332) \)に従う。
よって、\(Y\)の平均（期待値）は\(200000 \times 0.4332 = 86640\)。（答）

(2) 母平均\(m\)、母標準偏差\(\sigma\)の母集団から\(n\)個の標本を抽出したとき、標本平均\( \overline{W} \)は近似的に
正規分布\(\displaystyle N ( m , \frac{\sigma^2}{n} ) \)に従う。（答）

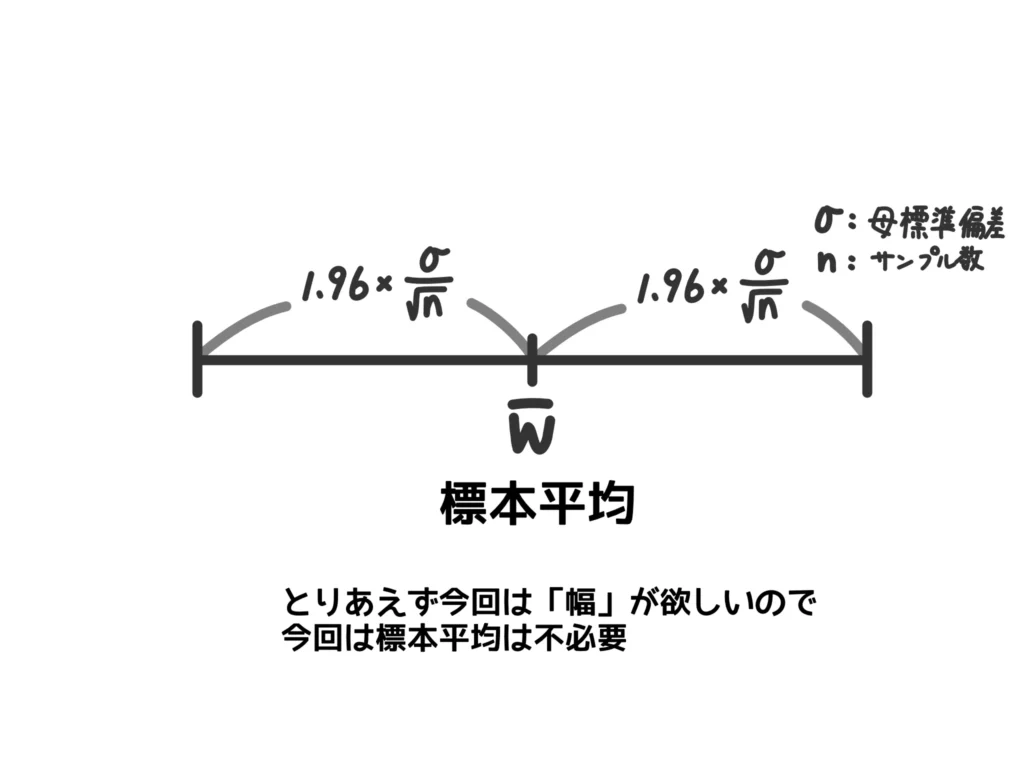
よって、95%の信頼区間の幅は\(\displaystyle 2 \cdot 1.96\frac{\sigma}{\sqrt{n}} = 3.92\frac{\sigma}{\sqrt{n}}\)。（答）

この幅を4(g)以下にしたいので、\(\sigma = 20\)とすると、
\(\displaystyle 3.92\frac{20}{\sqrt{n}} \leq 4\)
\(\displaystyle ( 3.92 \cdot 20 )^2 \leq 16 n\)
\(\displaystyle \Big( \frac{3.92 \cdot 20}{4} \Big)^2 \leq n \)
\(\displaystyle 19.6^2 \leq n \)
\( 384.16 \leq n\)。よってこの不等式を満たす最小の\(n\)を\(n_0\)とすると、\(n_0 = 385 \)。（答）

(3) 「今年収穫されるレモンの重さの母平均\(m\)(g)が過去の平均110gよりも軽い」というのが検証したい対立仮説なので「\(m<110\)」。（答）
標本の大きさ400は十分に大きいので、標本平均\( \overline{W} \)は近似的に
正規分布\(\displaystyle N ( m , \frac{\sigma^2}{n} ) = N ( 110 , \frac{20^2}{400} ) = N(110,1) \)に従う。（答）

\(\displaystyle Z_2 = \frac{\overline{W}-110}{1} = \overline{W}-110\)とすると、\(Z_2\)は標準正規分布\( N ( 0 , 1 ) \)に従う。
\( P ( \overline{W} \leq 108.2) = P( Z_2 \leq 108.2-110) = P ( Z_2 \leq -1.8) \)
\( P ( Z_2 \leq -1.8) = P(Z_2 \geq 1.8) \)なので、標準正規分布表から\(0.5 – 0.4641 = 0.0359\)。（答）
これは有意水準5%より小さいので帰無仮説は棄却される。（答）
（重さの平均が110gだと仮定すると、約3.6%しか起こらないこと（平均108.2）が起きてしまった。）
よって、今年収穫されるレモンの重さの母平均は110gより軽いと判断できる。（答）

共通テスト数学ⅡB．第6問【ベクトル】

(1)

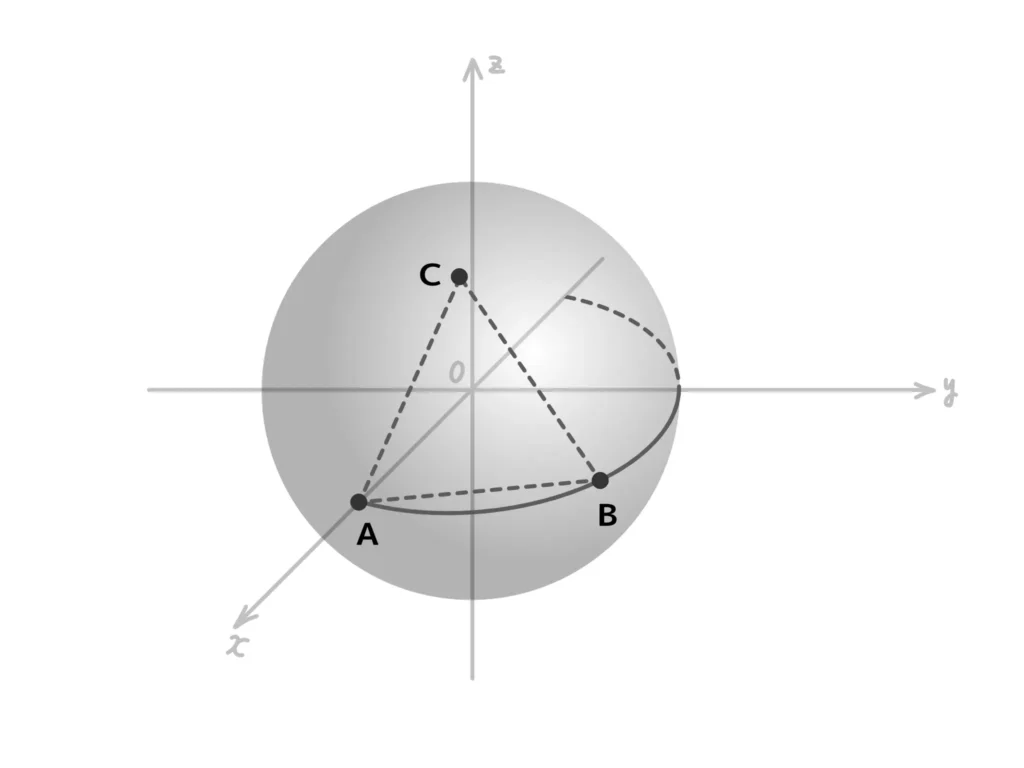
\(C\)が\(S\)上にあるとき、\( | \overrightarrow{OC} |^2 = 1 \)。

△OACと△OABが合同であるとき、対応する辺と角の大きさがそれぞれ等しいので、
\( \overrightarrow{OA} \cdot \overrightarrow{OC} =\overrightarrow{OA} \cdot \overrightarrow{OB} \)。（答）
\( \overrightarrow{OA} = (1,0,0) \)、
\( \overrightarrow{OB} = (a,\sqrt{1-a^2},0) \)、
\( \overrightarrow{OC} = (x,y,z) \)より、
\( \overrightarrow{OA} \cdot \overrightarrow{OC} = x\)、\( \overrightarrow{OA} \cdot \overrightarrow{OB} = a\)なので\(x=a\)…②。（答）

同様に△OBCと△OABも合同なので、
\( \overrightarrow{OB} \cdot \overrightarrow{OC} =\overrightarrow{OA} \cdot \overrightarrow{OB} \)。
\( \overrightarrow{OB} \cdot \overrightarrow{OC} = ax + y\sqrt{1-a^2}\)なので、
\( ax + y\sqrt{1-a^2} = a \)…③。（答）

(2)(i) \(\displaystyle a = \frac{3}{5} \)のとき、②、③より
\(\displaystyle x = \frac{3}{5} \)、\(\displaystyle \frac{3}{5} \cdot \frac{3}{5} + y\sqrt{1-\Big( \frac{3}{5} \Big)^2} = \frac{3}{5} \)。
これらを解いて、\(\displaystyle x = \frac{3}{5} \)、\(\displaystyle y = \frac{3}{10} \)。（答）

このとき、\(x^2 + y^2 + z^2 =1\)…①を満たす\(z\)が存在するか確認する。
\(\displaystyle x = \frac{3}{5} \)、\(\displaystyle y = \frac{3}{10} \)を代入すると、
\(\displaystyle \frac{45}{100} + z^2 =1\)
\(\displaystyle z^2 =1-\frac{45}{100} > 0 \)、つまり、これを満たす\(z\)はちょうど二つある。（答）

(ii) ①（\( z^2 =1 – ( x^2 + y^2 ) \)）を満たす実数\(z\)がいくつあるか？は\(x^2 + y^2\)が1を超えるかどうか？による。（1より大きければ\(z\)は存在しない。1であれば一つ、1より小さければ二つ）
\(\displaystyle a = -\frac{3}{5} \)のとき、同様に解くと、
\(\displaystyle x = -\frac{3}{5} \)、\(\displaystyle y = -\frac{6}{5} \)。\( |y| > 1\)なので\(x^2 + y^2\)は1を超える。よって、①を満たす実数\(z\)は存在しない。（答）

(3) (2)(ii)の考え方で検証すればよい。②、③より、
\(\displaystyle x =a\)、\(\displaystyle y = \frac{a(1-a)}{\sqrt{1-a^2}} \)。
①より、
\(\displaystyle z^2 =1 – x^2 – y^2 = 1-a^2-\frac{a^2(1-a)^2}{1-a^2} \)
\(\displaystyle \quad = \frac{(1-a^2)^2-a^2(1-a)^2}{1-a^2} \)
\(\displaystyle \quad = \frac{2a^3-3a^2+1}{1-a^2} \)
\(\displaystyle \quad = \frac{(a-1)(2a^2-a-1)}{-(a+1)(a-1)} \)
\(\displaystyle \quad = \frac{-(2a+1)(a-1)}{a+1} \)
\(\displaystyle \quad = \frac{(1+2a)(1-a)}{a+1} \)。（答）

分母である\(a+1 >0\)なので、分子である\( (1+2a)(1-a) \geq 0 \)となることが△ABCが正三角形となる点Cがあるための必要十分条件である。
これを解いて\(\displaystyle \frac{1}{2} \leq a \leq 1 \)。\(-1 < a < 1\)より、\(\displaystyle \frac{1}{2} \leq a < 1 \)。（答）

共通テスト数学ⅡB．第7問【複素数平面】

(1) \( \alpha = 3+2i\)、\(\beta = 7\)、\(\gamma = 7 + 10i\)のとき、
\( \gamma – \alpha = 4 + 8i \)
\( \beta – \alpha = 4 – 2 i \)。（答）
\(\displaystyle \frac{\gamma – \alpha}{\beta – \alpha} = \frac{4+8i}{4-2i} = 2\cdot \frac{1+2i}{2-i}\)
\(\displaystyle \quad = 2\cdot \frac{(1+2i)(2+i)}{(2-i)(2+i)}=2\cdot \frac{5i}{5} = 2i \)。（答）

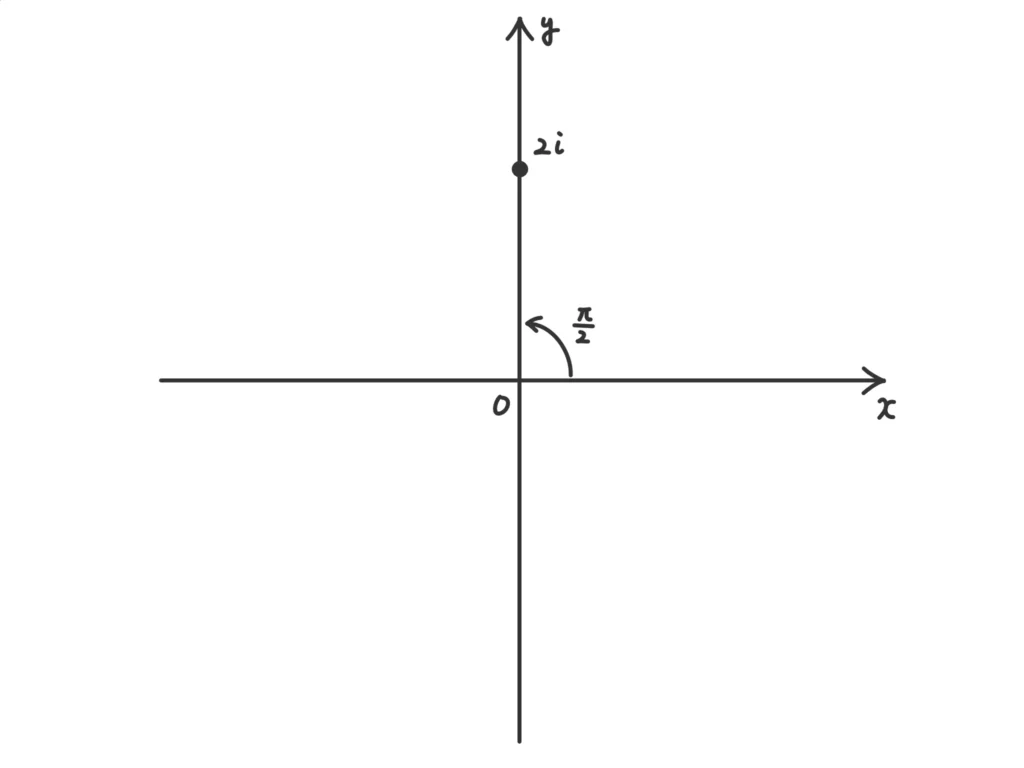
偏角は\(\displaystyle \frac{\pi}{2}\)。（答）

(2) \(w\)の偏角が\(\displaystyle \frac{\pi}{2}\)または\(\displaystyle \frac{3}{2}\pi \)のとき、\(w\)は純虚数となる。（答）
このとき、\(w + \overline{w} = 0\)（\(w = -\overline{w}\)と覚えている人もいるかも。\(w = ai\)と置けばすぐに示せる性質です）。（答）

(3) (i)（…最初は省略…）
\(\displaystyle 2 + \frac{2}{z} + \frac{2}{\overline{z}} = 0\)
\( z\overline{z} + \overline{z} + z = 0 \)
\( (z+1)\overline{z} + z = 0 \)
\( (z+1)\overline{z} + z+1 = 1 \)
\( (z+1)(\overline{z} + 1) = 1 \)
\( (z+1)(\overline{z + 1}) = 1 \)
\( |z+1|^2= 1 \)
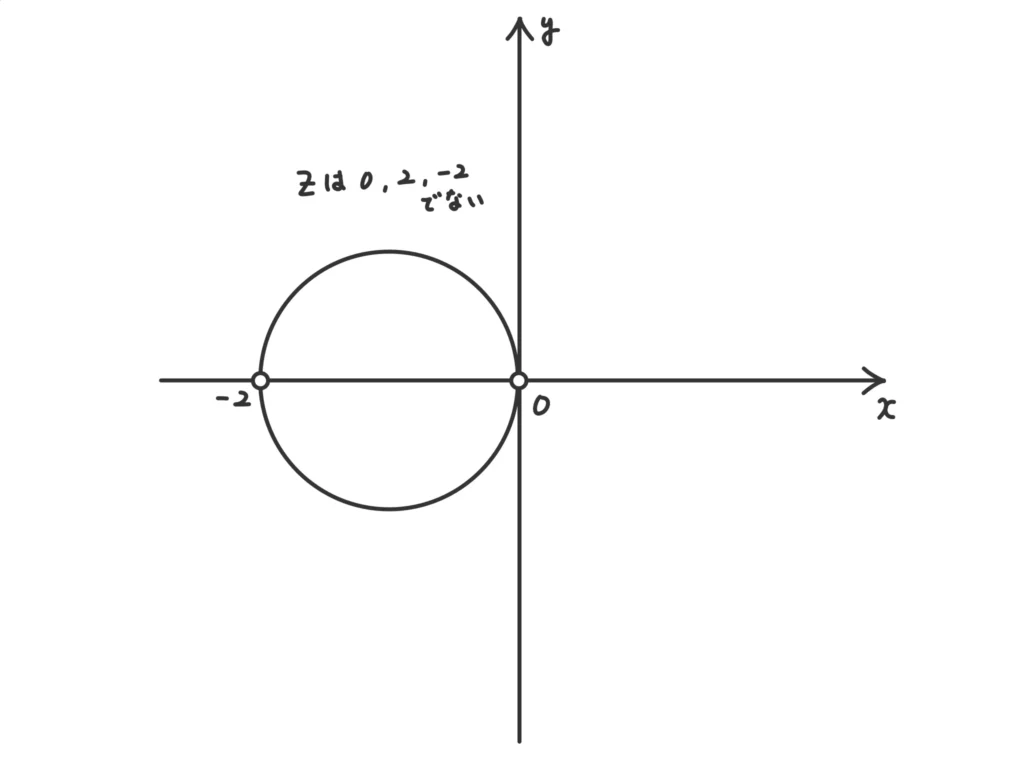
\( |z+1|= 1 \)。（答）
コレを図示すると次のようになる。

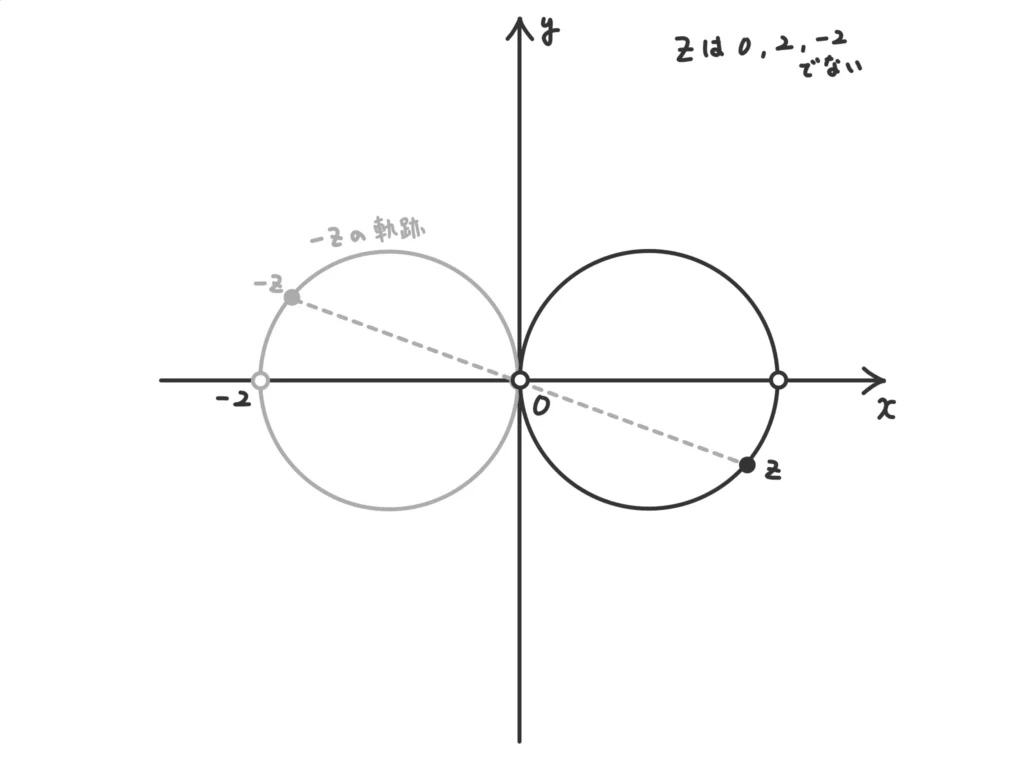
(ii) \(\alpha\)、\(\beta\)、\(\gamma\)をそれぞれ\(-1\)倍した \(-\alpha\)、\(-\beta\)、\(-\gamma\)で考えると、
\(\displaystyle \frac{(-\gamma) – (-\alpha)}{(-\beta) – (-\alpha)} = \frac{\gamma – \alpha}{\beta – \alpha}\)なので、点\(z\)を平面上に図示すると(i)と同じになる。（答）

(iii) 点\(z\)に対して、点\(-z\)は原点対称な点。また、今回は\(-z\)を図示すると(i)と同じになる。（\(z\)が0,2,-2でない複素数なら、\(-z\)も0,2,-2でない複素数。）

つまり、点\(z\)は(i)の図形を原点対称に移動した図になる。（答）

2025共通テスト「数学ⅡBC」解説まとめ

2025年共通テスト「数学ⅡBC」の解説でした。

新課程で初めての共通テストだったので、やや簡単だったかな、という感じですが、今後の共通テストの方針が見えるメッセージ性のある問題が多かった印象です。