三角比の表が覚えられない！？【ポイントを押さえれば覚えなくてOKです】

三角比の表は、よく「覚えなさい」と言われますが…

あの表を覚えるの、大変ですよね。少なくとも私には全部暗記するのはムリです。

この記事では、三角比の表と、その覚え方のコツについて説明していきます。

三角比の表

三角比の表…あれ、覚えるの大変ですよねぇ。

ちなみに、三角比の定義やなぜ三角比を使うのか？についてはこちらの記事をご覧ください。

実際、三角比の値は「\(\sin{}\)？\(\cos{}\)？\(\tan{}\)？どれなのか？」と「角度」によって決まります。

	0°	30°	45°	60°	90°	120°	135°	150°	180°
\(\sin\)	\(0\)	\(\displaystyle \frac{1}{2}\)	\(\displaystyle \frac{1}{\sqrt{2}}\)	\(\displaystyle \frac{\sqrt{3}}{2}\)	\(1\)	\(\displaystyle \frac{\sqrt{3}}{2}\)	\(\displaystyle \frac{1}{\sqrt{2}}\)	\(\displaystyle \frac{1}{2}\)	\(0\)
\(\cos\)	\(1\)	\(\displaystyle \frac{\sqrt{3}}{2}\)	\(\displaystyle \frac{1}{\sqrt{2}}\)	\(\displaystyle \frac{1}{2}\)	\(0\)	\(\displaystyle -\frac{1}{2}\)	\(\displaystyle -\frac{1}{\sqrt{2}}\)	\(\displaystyle -\frac{\sqrt{3}}{2}\)	\(-1\)
\(\tan\)	\(0\)	\(\displaystyle \frac{1}{\sqrt{3}}\)	\(1\)	\(\sqrt{3}\)	なし	\(-\sqrt{3}\)	\(-1\)	\(\displaystyle -\frac{1}{\sqrt{3}}\)	\(0\)

さて、この表、よく先生に

と言われるやつですね。

ですが、

と悩む生徒も多いです。

実はこの三角比の値、覚えるのにコツがあるんです。

三角比の表は覚えなくていい？

個人的にはポイントになる値だけ覚えればいいと思います。

表を丸暗記…はやめておいた方がいいと思います。

sin、cosは値と長さの大小関係を覚える

まずは\(\sin\)、\(\cos\)です。こちらの方が覚えにくい、と感じる人が多いんじゃないでしょうか？

では三角比の値のポイントは？というと、

値と辺の長さの大小関係だけ覚えておく

ということです。

三角比には45°、135°、…の45°系と30°、60°、…の30°系があります。

45°系は\(\sin\)の値も\(\cos\)の値も\(\displaystyle \frac{1}{\sqrt{2}}\)なので、値を覚えるのはあまり難しくありません。

問題は30°系ですね。こちらは\(\displaystyle \frac{1}{2} < \frac{\sqrt{3}}{2}\)の大小関係と辺の長さの大小関係を覚えておきましょう。

あとはこちらの記事で説明した通り、単位円を使って（イメージして）

「長い方」=\(\displaystyle \frac{\sqrt{3}}{2}\)、「短い方」=\(\displaystyle \frac{1}{2}\)、

と判断しましょう。

正直、単位円を使って判断できた方がいいです。この後、数Ⅱで弧度法を勉強したら、なおさらこちらの判断方法の方が有利です。

tanは傾き

では\(\tan\)は？というと、

\(\tan\)＝傾き

で判断しましょう。実際に「\(\tan\)は傾き」という側面があるので、傾き具合で判断します。

\(\tan\)の代表値と大小関係は

\(\displaystyle \frac{1}{\sqrt{3}} < 1 < \sqrt{3} \)

ですが、特に45°の傾きは1だ、というのが判断基準になります。この45°よりも

傾きが小さければ\(\displaystyle \frac{1}{\sqrt{3}}\)、傾きが大きければ\(\sqrt{3} \)

と判断します。

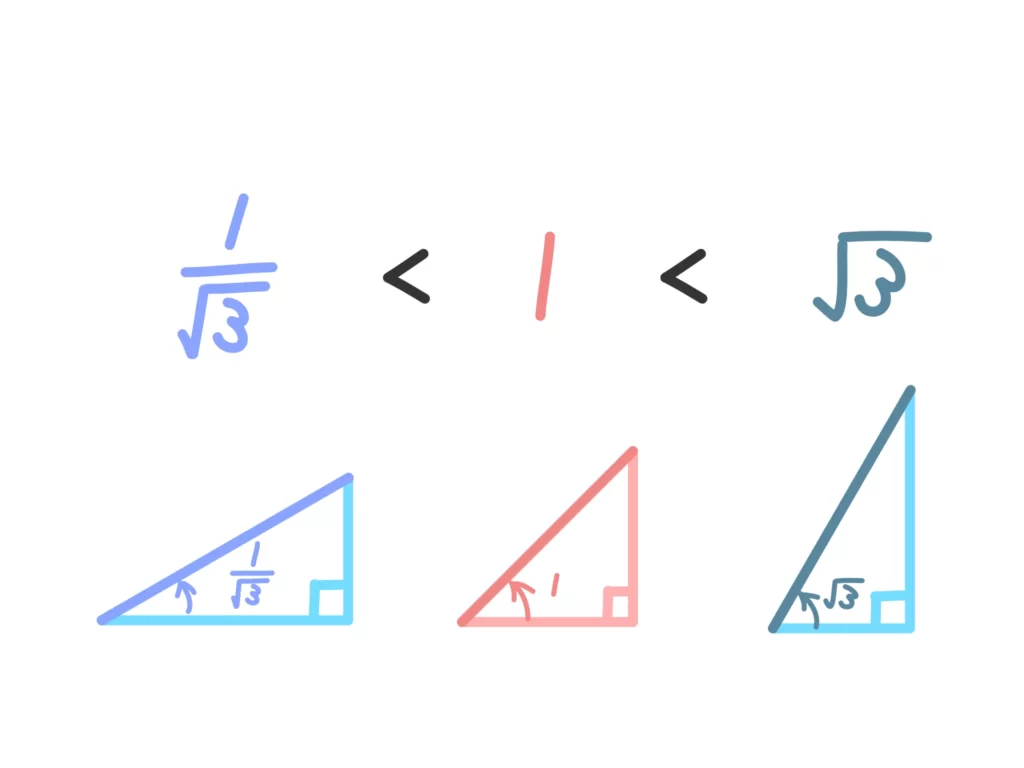
こんな感じで三角比（関数）の値を判断することができれば、180°を超える角度の三角関数の値も、弧度法での判断も早く、正確になります。

三角比の値のまとめ

三角比の値の覚え方のコツでした。

とりあえず丸暗記…はオススメしません。

• \(\sin\)、\(\cos\)は\(\displaystyle \frac{1}{2} < \frac{1}{\sqrt{2}} < \frac{\sqrt{3}}{2}\)の大小関係と辺の長さを覚えておく。
• 「\(\tan\)は傾きだ」というのと、\(\displaystyle \frac{1}{\sqrt{3}} < 1 < \sqrt{3} \)の大小関係を覚えておく。

というのを押さえておいて、あとは単位円を使ってその都度判断する方がいいかな？と思います。