漸化式って？【漸化式の基本パターンから解き方の総まとめ！】

漸化式…ある程度数列の勉強を進めると出てくるのですが、最初はその必要性がわかりにくいです。

この記事では、漸化式の基本的な考え方からその必要性、基本パターンの解き方まで説明していきます。

漸化式とは？

ということで漸化式です。

今回の茶番に関しては後述する「漸化式の必要性」のところで少しお話ししていきたいと思います。

漸化式とは、数列の\(n\)番目の項と\((n+1)\)番目の項（場合によっては\((n+2)\)番目の項も）の関係を表した式です。

例えば、数列\(\{a_n\}\)に関して次のような漸化式が与えられたとしましょう。

\(a_{n+1} = a_n + 2\)

これは、「\((n+1)\)番目の項は\(n\)番目の項（ひとつ前の項）に２を足して得られる」という意味なので、\(\{a_n\}\)は「公差が２の等差数列だ」ということがわかります。

\(\{a_n\}\)が等差数列だ、ということがわかったので、この式に初項\(a_1\)の情報があれば一般項を求めることができます。

\(\begin{cases}
a_{n+1}= a_n+2\\
a_1 = 1
\end{cases}\)

この式を読み解くと、\(\{a_n\}\)は「初項が１、公差が２の等差数列だ」ということがわかるので、一般項は、

\(a_n = 1 + (n-1)2 = 2n-1\)

となります。

このように、漸化式の情報から数列の一般項を求めることを「漸化式を解く」といいます。

漸化式の必要性

と思う人もいるかもしれません。

確かに、等差数列くらいだったらわざわざ漸化式を解く必要はないかもしれません。

というか、「あれって漸化式を解いて一般項をだしてるのか？ただ、等差数列だって読み解いただけじゃん…」と思う人もいるでしょう。

例えば冒頭の例「今日晴れで３日後も晴れである確率」なんかは、ガチンコで計算しようとするとかなり大変です。

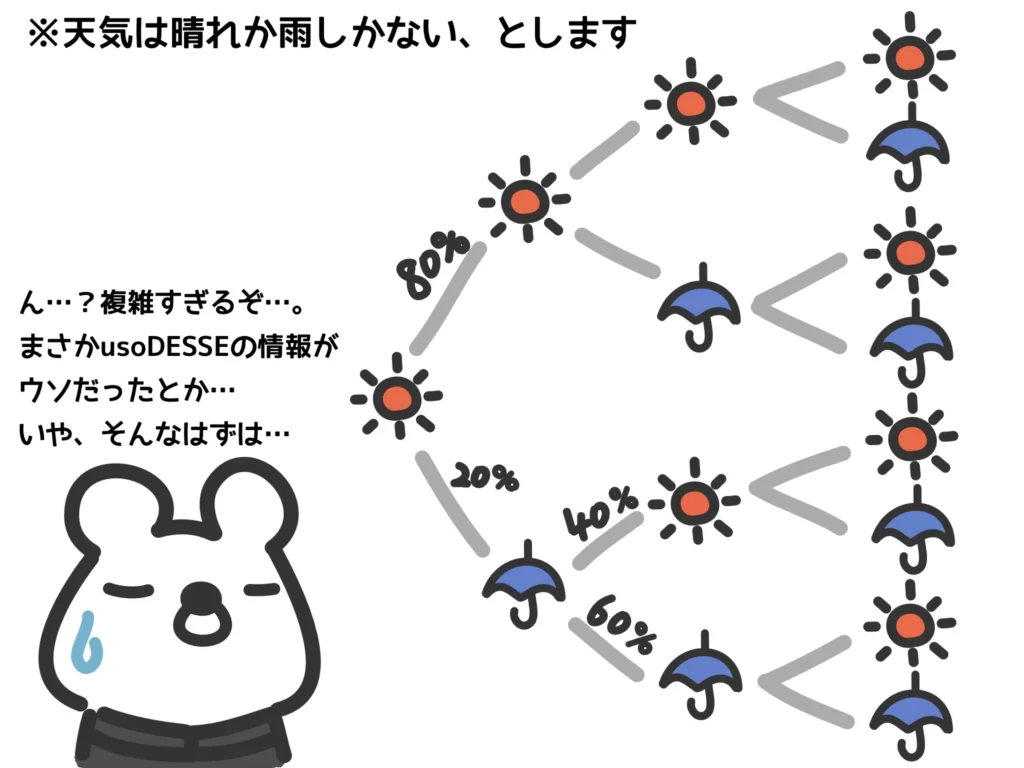
こんなときは漸化式の出番です。全てのパターンを網羅するのはかなり大変ですが、\(n\)日目と\((n+1)\)日目だけに着目すれば、実は簡単に漸化式を立てることができます！

\(\displaystyle p_{n+1} = \frac{80}{100} p_n + \frac{40}{100} (1-p_n)\)

このように、「複雑な事象でも、\(n\)番目と\((n+1)\)番目に焦点を当てれば簡単に立式できる」という状況があります。こんなときには漸化式が便利です！

また、有名な数列「フィボナッチ数列」は

\(1, 1, 2, 3, 5, 8, 13, 21, 34, \cdots\)

こんな感じの数列ですが、この数列の作り方は「１つ前と２つ前の項を足す」という規則でできています。数列を作る規則としては難しくないですよね？

ですが、「じゃあ一般項は？」と言われたら、等差数列でも等比数列でもないし、階差数列を使っても解くことができません。

そこで漸化式の出番です。このフィボナッチ数列は

\(\begin{cases}
a_{n+2}= a_{n+1}+a_n\\
a_1 = 1, a_2 = 1
\end{cases}\)

という漸化式を立てることができます。

このような \(a_n\)、\(a_{n+1}\)、\(a_{n+2}\)の３つの項の関係を表した漸化式を三項間漸化式と言いますが、これも解くことができて一般項を求められます。

この後、漸化式の基本パターンを押さえますが、漸化式が本領を発揮するのは

• 複雑な形で漸化式が与えられている。もしくは、漸化式じゃないと立式できないケース（今回の天気の話のように）がある。
• ちょっとした（かなり複雑な…ということもありますが）操作をすることで、基本パターンに帰着できる。
• 漸化式を解くことで一般項を求めることができる。

つまり、より複雑な数列についても漸化式を解くことで一般項を求めることができる、というのが漸化式の最大のメリットですね。

漸化式の基本パターン

ということで、漸化式の基本パターンを押さえておきます。

形がかなり重要です。ちょっとでもこの形から外れると上手く解けません。

等差数列

\(a_{n+1} = a_n + d\)の形は等差数列

「\(d\)は定数」というところと、その\(d\)の値が公差になる、というところを押さえておいてください。

例．\(\begin{cases}
a_{n+1}= a_n+2\\
a_1 = 1
\end{cases}
\rightarrow a_n = 1 + (n-1)2=2n-1\)

等比数列

\(a_{n+1} = r a_n \)の形は等比数列

「\(r\)は定数」というところと、その\(r\)の値が公比になる、というところを押さえておいてください。

例．\(\begin{cases}
a_{n+1}= 3a_n\\
a_1 = 2
\end{cases}
\rightarrow a_n = 2\cdot 3^{n-1} \)

階差数列

\(a_{n+1} = a_n + (nの式)\)の形は階差数列利用

このパターンは忘れられがちですが結構重要です。複雑な漸化式を、このパターンに帰着させることも多いです。

この漸化式を\(a_{n+1}-a_n=(nの式)\)と変形すればわかりますが、こちらの記事でも説明した通り、このとき\((nの式)\)の部分が階差数列\(\{b_n\}\)の一般項となります。

よって、\(n \geq 2\)のとき、\((nの式)=b_n\)とすると、

\(\displaystyle a_n = a_1 + \sum_{k=1}^{n-1}b_k\)

として一般項を求めることができます。

例．\(\begin{cases}
a_{n+1}= a_n + 2n -1\\
a_1 = 1
\end{cases}\)
\( \rightarrow n \geq 2\)のとき、
\(\displaystyle a_n = 1 + \sum_{k=1}^{n-1}(2k-1)=\cdots= n^2-2n+2 \)
これは\(n=1\)のときも成り立つ。
よって\(\displaystyle a_n= n^2-2n+2 \)

\(a_{n+1}=a_n+(nの式)\)の形と、\((nの式)\)の部分が階差数列の一般項になる、という点は押さえておきましょう。

a_n+1 = pa_n+qの形

超重要な形です。見た目は等差数列と等比数列を合わせたような式です。

例．\(a_{n+1} = 3a_n +4\)

この漸化式の解き方は非常に重要で、複雑な形をした漸化式もこのタイプに帰着されることが多いです。多分一番この形に帰着されます。

特性方程式と言われる式を使って変形して解くのですが、重要すぎるので別の記事にまとめておきます。

まとめ

漸化式の考え方と基本パターンのまとめでした。

こちらの記事で解く漸化式が基本パターンで一番重要、といっても過言ではないのでこちらも合わせてご覧ください。