PR
二次関数で判別式を使う時って?【二次関数と判別式の関係を徹底解説!】
二次関数の問題で有効な手段である判別式…。
ですが、この判別式、意味をしっかりと理解して使わないとなかなか思うように問題が解けません。
この記事では、二次関数と判別式の本質的なつながりについてわかりやすく説明していきたいと思います。
二次関数と判別式の関係
 たろぅ
たろぅふん…やっぱりそんなもんかよ…。



どうしたの?



今話題のメジャーリーガー尾々谷熊平(ゆうへい)選手、家賃100万円の家に住んでるらしいぜ!高すぎだろ!贅沢すぎるぜ!



…400円よ。



ん?なにが?今日の弁当代?今どき400円じゃ大した弁当買えないよ?



彼の年俸85億円を一般的な彼の同年代の平均年収340万円に換算すると、400円程度の家賃の家に住んでる計算よ?



…今どき400円じゃ腹も満たされねぇよ?ハングリー精神の塊か?
ということで(?)二次関数と判別式の関係です。
結論から言うと、この2つは密接に関係していますが、実はしっかりと読み替えることが重要です。
そこの理解を深めないままサラッと二次関数の問題に判別式を持ち込むと後々困ることになります。
このタイミングでしっかりと二次関数(関数)と判別式(方程式)の言い換えについて理解していきましょう。

判別式とは?
まずは判別式のおさらいです。
判別式
二次方程式\(a x^2 +b x + c = 0\)について、判別式\(D = b^2 -4ac\)とすると、判別式の条件と二次方程式の実数解の個数は次のようになります。
| 判別式 | 実数解の個数 |
|---|---|
| \(D > 0\) | 2個 |
| \(D = 0\) | 1個(重解) |
| \(D < 0\) | 0個(虚数解2個) |
これは、判別式が二次方程式の解の公式\(\displaystyle x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\)の\(\sqrt{\quad}\)の中身だからです。
なので、二次方程式\(a x^2 +2b’x+c =0\)の場合は\(D\)の代わりに\(D/4 = b’^2-ac\)を使ってもOKです。
この判別式は「二次方程式の解の個数を調べる」という意味しかありません。
ですが、この判別式は「二次関数」の問題でも頻繁に顔を出します。



二次方程式と二次関数…まぁ似たような感じじゃん。なにか違うの?一緒でしょ。「二次」だし。



そういう風に雑な解釈をしていると「100万円の家賃が(彼にとって)高い、贅沢だ」という勘違いをするんですよ。
きちんと二次方程式でできること、二次関数でできることの区別をつけてください。



…はい。
二次関数の問題で判別式を使うのはどんな時?
結論から言うと判別式は「二次関数と一次関数(もしくは二次関数)のグラフの交点の個数を求める」際に使います。
「交点を持つかどうか?」や「交点を常に持つことを示せ」というタイプの問題でも使います。「交点を持つかどうか=交点が0個かそうじゃないか」と言い換えることができるので、判別式で判断することができるからです。



それでは一つ例題を挙げてみましょう。
例.\( y = x^2 -ax + a+3\)のグラフと\(x\)軸との交点の個数を求めよ。



はい、じゃあたろうくん解いてください。



え…なんかヤダな。
二次関数の問題で判別式を使う際の注意点
二次関数の問題で判別式を使う際に最も注意すること…それは、
二次関数はあくまで「関数」の話で、判別式は二次方程式、つまり「方程式」の話だ、
という点です。ここを意識してください!



では今解いてもらったたろうくんの解答の間違いを見てみましょう。



(え?間違えてるって決めつけた?)いや…まぁまぁ自信あるんですけど。
例.\( y = x^2 -ax + a+3\)のグラフと\(x\)軸との交点の個数を求めよ。
(解答)
判別式\(D = a^2 – 4 \cdot 1 \cdot (a+3) = a^2 -4a-12=(a+2)(a-6)\)
よって、
\(D > 0\)つまり\(a<-2,6<a\)のとき、交点は2個
\(D = 0\)つまり\(a=-2,6\)のとき、交点は1個
\(D < 0\)つまり\(-2<a<6\)のとき、交点は0個 …(答)
ハッキリ言ってほとんど問題ないですが、やはり解答の最初に
「もう少し二次関数と二次方程式の違いを意識してほしいなぁ…」
という部分があります。
それは、いきなり「判別式」と書いてあるという点です。
先ほども言いましたが、判別式は「二次方程式の実数解の個数を調べる」という意味しかありません。
この問題にはまず二次方程式が与えられていません。あるのは二次関数です。
それと、「判別式\(D > 0\)のとき交点2個」というのもどうでしょうか?判別式で調べられるのは二次方程式の実数解の個数です。\(x\)軸との交点の個数が調べられるわけではありません。



ほとんど◯の解答ですが、端々に「ちゃんと理解してるのかな…」という点が見られます。そこをフォローしていきましょう。
(解答)
二次方程式\( x^2 -ax + a+3 = 0\)の判別式を\(D\)とする。
判別式\(D = a^2 – 4 \cdot 1 \cdot (a+3) = a^2 -4a-12=(a+2)(a-6)\)
よって、
\(D > 0\)つまり\(a<-2,6<a\)のとき、交点は2個
\(D = 0\)つまり\(a=-2,6\)のとき、交点は1個
\(D < 0\)つまり\(-2<a<6\)のとき、交点は0個 …(答)
解答としてはこのくらいでしょう。もしかしたら最初の解答でも◯を貰えるかもしれません。「判別式\(D > 0\)のとき交点2個」というのもどうでしょうか?と言いましたが、正直そこを詳しく書く必要もないと思います。



いや…じゃあ全然最初の解答でOKじゃん。なんなの?言いがかりつけてんの?
と思うかもしれませんが、では、なぜ「\( x^2 -ax + a+3 = 0\)」なのでしょうか?もとは\( y = x^2 -ax + a+3\)だったのに、勝手に二次方程式\( x^2 -ax + a+3 = 0\)としていいんでしょうか?\(=0\)ってなんですか?



ん…?そりゃ…だって二次方程式だから\(=0\)でしょ?
判別式は二次方程式の実数解の個数しか調べられないのに、それを交点の個数って言っていいんですか?



いや…まぁ…いいんじゃない?解の個数も交点の個数も一緒でしょ?…多分。
このあたりをきちんと説明できれば問題ないのですが、曖昧にしていると後で困ります。ここの関数と方程式の対応をしっかりと理解しましょう!解答にはありませんが、重要な考え方を説明していきます。



はーい。
先程の解答にさらに注釈を入れるとこんな感じになります。
(考え方)
まず「交点の個数」と言っていますが、そこを一歩踏み込んで「交点の座標を求める」ことを考えてみましょう。
交点の座標を求めるためには2つのグラフを表す関数を連立してあげる必要があります。連立には「同時に満たす値を求める」という意味があるからです。これが交点(同時に満たす点)の意味と一致します。
つまり、正確に言うと、関数\(y=x^2 -ax + a+3\)と\(y=0\)(\(x\)軸)を連立した
\(\begin{cases}
y= x^2 -ax + a+3\\
y = 0
\end{cases}\)
つまり、二次方程式\( x^2 -ax + a+3 = 0\)を解けばグラフの交点の\(x\)座標を求めることができます。
ただし、今回は「交点の個数」が必要なだけなので判別式だけで十分です。
なぜなら、「実数解の個数」=「交点の\(x\)座標の個数」=「交点の個数」となるからです。



この
「二次関数の交点の\(x\)座標↔二次方程式の解」
「二次関数の交点の個数↔二次方程式の実数解の個数」
という関数と方程式の言い換えをしっかりと意識してください!
(解答)
二次方程式\( x^2 -ax + a+3 = 0\)の判別式を\(D\)とする。(←交点を求めるために連立した二次方程式を考える)
判別式\(D = a^2 – 4 \cdot 1 \cdot (a+3) = a^2 -4a-12=(a+2)(a-6)\)
よって、
\(D > 0\)つまり\(a<-2,6<a\)のとき、交点は2個
\(D = 0\)つまり\(a=-2,6\)のとき、交点は1個
\(D < 0\)つまり\(-2<a<6\)のとき、交点は0個
(↑二次方程式の実数解の個数=交点の\(x\)座標の個数=交点の個数)
…(答)
二次関数のグラフが上に凸でも判別式は有効?
ときどき「上に凸でも判別式を使って解けるんですか?」という質問を聞きます。これは「二次関数のグラフの頂点の\(y\)座標と判別式は同じ役割をする」という説明を聞いたときに思い浮かぶ質問だと思います。
上でかなり丁寧に考えたのでもうわかると思いますが、上に凸であろうが下に凸であろうが「交点の個数=交点の\(x\)座標の個数=二次方程式の実数解の個数」なので、判別式で解くことができます。
もちろん判別方法も上に凸であろうが下に凸であろうが
\(D>0\)のとき実数解の個数2個、つまり交点2個。
\(D=0\)のとき実数解の個数1個、つまり交点1個。
\(D<0\)のとき実数解の個数0個、つまり交点0個。
となります。
二次関数のグラフの頂点と判別式の関係
二次関数のグラフと\(x\)軸との交点の個数を判断する上で、
グラフの頂点の\(y\)座標と判別式は同じ役割をします。
一般的な二次関数\(y = ax^2+bx+c\)と\(x\)軸の交点の個数を考えます。
先ほど言ったように下に凸でも上に凸でも\(ax^2+bx+c=0\)の判別式\(D=b^2-4ac\)を使えば
\(D=b^2-4ac>0\)のとき実数解の個数2個、つまり交点2個。
\(D=b^2-4ac=0\)のとき実数解の個数1個、つまり交点1個。
\(D=b^2-4ac<0\)のとき実数解の個数0個、つまり交点0個。
でOKです。
一方、グラフの頂点の\(y\)座標で考えてみましょう。下に凸でも上に凸でも頂点の\(y\)座標を求める方法は平方完成です。
\(y = ax^2+bx+c\)
\(\displaystyle \quad = a \Big( x^2 + \frac{b}{a}x \Big) + c \)
\(\displaystyle \quad = a \Big\{ \Big( x + \frac{b}{2a} \Big)^2-\frac{b^2}{4a^2} \Big\} + c \)
\(\displaystyle \quad = a \Big( x + \frac{b}{2a} \Big)^2-\frac{b^2}{4a} + c \)
\(\displaystyle \quad = a \Big( x + \frac{b}{2a} \Big)^2-\frac{b^2-4ac}{4a}\)
よって、頂点の\(y\)座標は\(\displaystyle -\frac{b^2-4ac}{4a}\)となります。
(i) 下に凸つまり\(a>0\)のとき
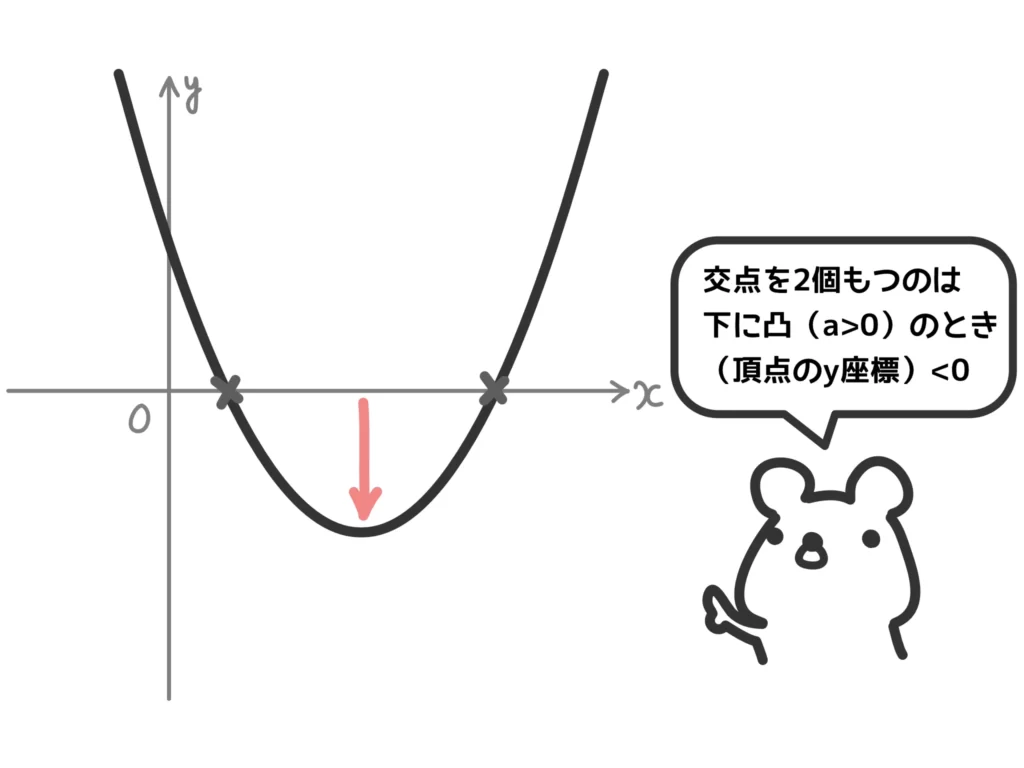

交点が2個となる条件は
\(\displaystyle -\frac{b^2-4ac}{4a} < 0\)
\(\displaystyle \frac{b^2-4ac}{4a} > 0\)
\(\displaystyle b^2-4ac > 0\)(\(4a > 0\)なので)
これは判別式\(D=b^2-4ac > 0\)の条件と一致します。
同様に交点が1個となるのは\(\displaystyle b^2-4ac = 0\)、交点が0個となるのは\(\displaystyle b^2-4ac < 0\)のときです。
(ii) 上に凸つまり\(a<0\)のとき
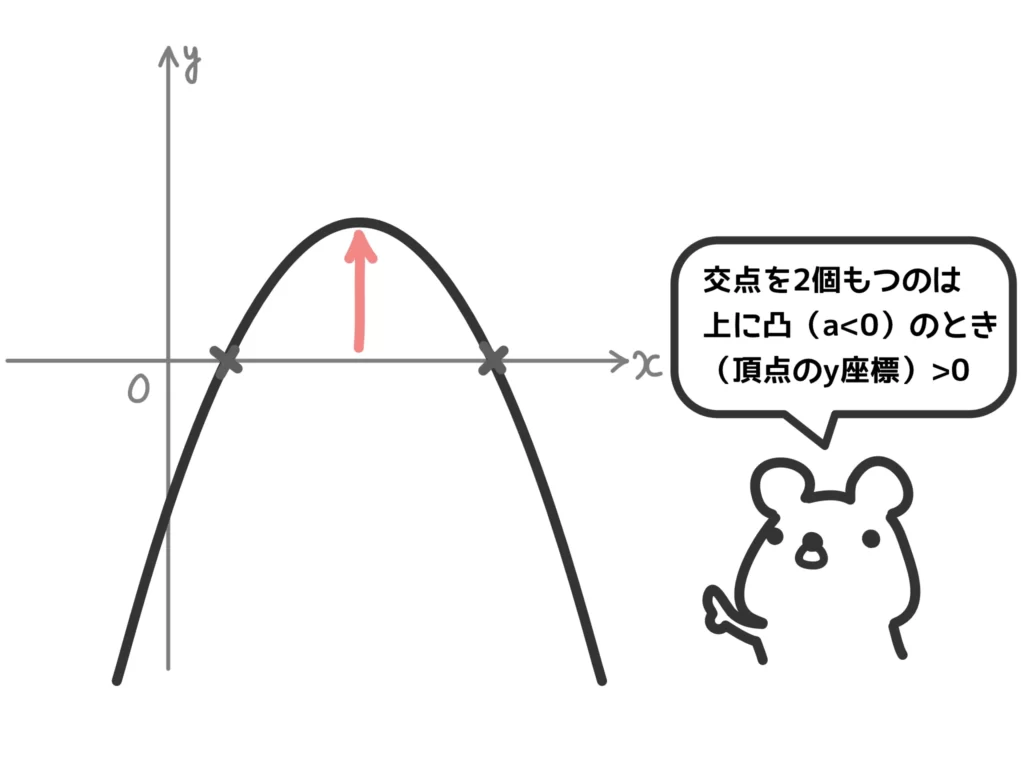

交点が2個となる条件は
\(\displaystyle -\frac{b^2-4ac}{4a} > 0\)
\(\displaystyle \frac{b^2-4ac}{4a} < 0\)
\(\displaystyle b^2-4ac > 0\)(\(4a < 0\)なので)
これは判別式\(D=b^2-4ac > 0\)の条件と一致します。
同様に交点が1個となるのは\(\displaystyle b^2-4ac = 0\)、交点が0個となるのは\(\displaystyle b^2-4ac < 0\)のときです。



下に凸か上に凸かで頂点の\(y\)座標の条件と\(a\)の正負が変わるのでちょっとゴチャゴチャしますが、最終的に判別式と同じ条件になるというのがわかります。
二次関数と判別式を使った問題
二次関数と判別式を使った例題をいくつか挙げましょう。



特に「関数↔方程式」の言い換えが重要になってくる問題を選んでみました!
例題1.\(y=x^2+2ax+a\)が表すグラフと\(y=2x+1\)の表すグラフの交点の個数を求めよ。
これは先程の問題の話がわかっていれば大丈夫です。
勢い余って「\(x^2+2ax+a=0\)の判別式を\(D\)とする…」として話を進めないようにしましょう。
(解答)
\(y=x^2+2ax+a\)と\(y=2x+1\)を連立して、
\(x^2+2ax+a=2x+1\)
\(x^2+2(a-1)x+a-1=0\)…①
この二次方程式の実数解の個数と2つのグラフの交点の個数は一致します。
①の判別式を\(D\)とすると、\(D/4=(a-1)^2-1\cdot (a-1) = (a-1)(a-2)\)
よって、
\(D/4 > 0\)つまり\(a<1,2<a\)のとき、交点は2個
\(D/4 = 0\)つまり\(a=1,2\)のとき、交点は1個
\(D/4 < 0\)つまり\(1<a<2\)のとき、交点は0個 …(答)
例題2.二次方程式\(x^2-(a+2)x-2a+1 = 0\)が\(x \geq 0\)で異なる2つの実数解を持つような\(a\)の値の範囲を求めよ。
今まではグラフの交点の話を方程式にもっていっていましたが、今度は逆パターンです。
二次方程式が単純に「異なる2つの実数解を持つような\(a\)の値の範囲」と言われれば判別式だけで十分ですが、今回のように「\(x \geq 0\)で」という条件がつくとなると話が別です。
例えば、異なる2つの解が\(x = -1,2\)などでは「\(x \geq 0\)で」という条件を満たさないからです。
ではどうするか?というと、グラフ(関数)の力を借ります。方程式の解を直接調べるのはかなり大変だからです。
ここでも「方程式↔グラフ(関数)」の言い換えを上手く利用していきます。
少し具体的に言い換えを説明すると「\(y = x^2-(a+2)x-2a+1\)と\(x\)軸が\(x \geq 0 \)で異なる2点で交わればよい」ということになります。
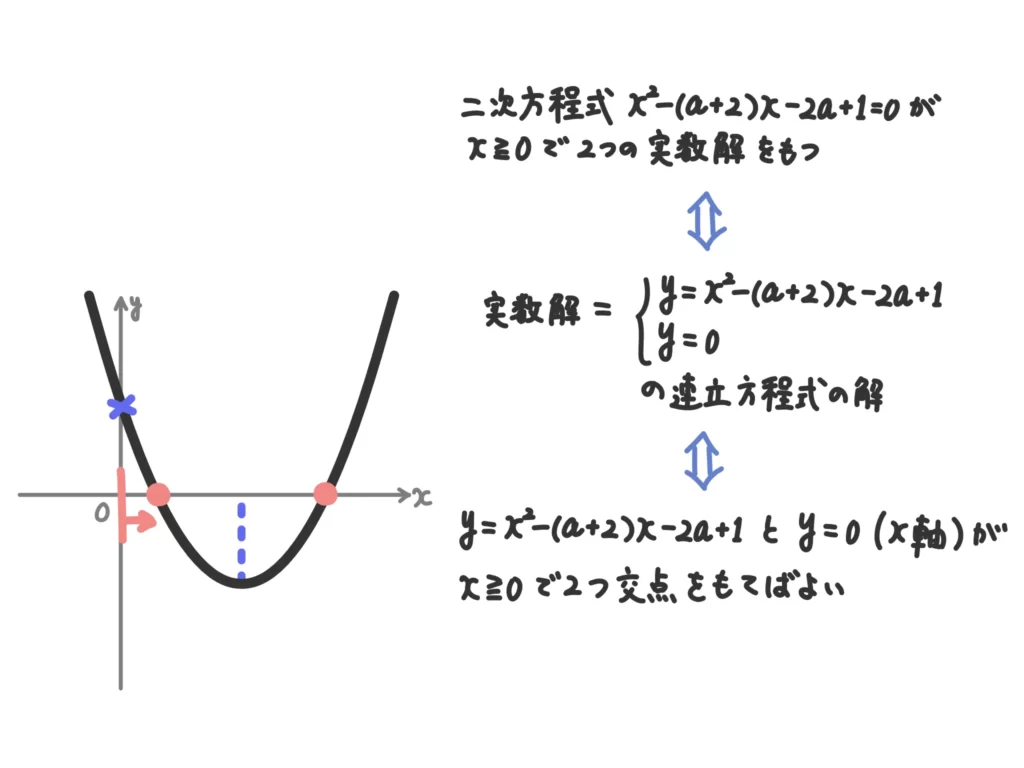




この問題を「解の配置問題」といいます。二次関数の応用問題としては定番ですね!この「解の配置問題」はグラフのパターンをイメージしつつ、以下の3点を考えましょう。条件によっては①だけで済むこともあります。
- 端点(問題の条件の境界)
- 判別式
- 軸
(解答)
\(x^2-(a+2)x-2a+1 = 0\)の判別式を\(D\)、\(f(x) = x^2-(a+2)x-2a+1\)とおくと、以下の3つの条件を満たせばよい。
\(\begin{cases}
f(0) \geq 0 \cdots ①\\
D > 0 \cdots ②\\
(軸) > 0 \cdots ③
\end{cases}\)
①より、\(-2a+1 \geq 0 \)、よって\(\displaystyle a \leq \frac{1}{2}\)…①’
②より、\(D = \{ -(a+2) \}^2 -4(-2a+1) > 0\)
\(a^2 + 12a > 0\)
\(a(a+12) > 0\)、よって\(a < -12, 0 < a\)…②’
③より、\(\displaystyle (軸)= \frac{a+2}{2} > 0 \)、よって\(a > -2 \)…③’
①’、②’、③’から、\(\displaystyle 0 < a \leq \frac{1}{2}\) …(答)
問.二次方程式\(x^2-(a+2)x-2a+1 = 0\)が\(0 \leq x \leq 3\)で解を持つような\(a\)の値の範囲を求めよ。
答え
\(\displaystyle 0 \leq a \leq \frac{4}{5}\)



最後に、判別式は使いませんが「関数↔方程式」の言い換えを上手く利用する問題を出しておきます。これも上手くグラフを利用すれば解けますが、いわゆる定数分離という手法を使うとキレイに解くことができます!
問.方程式\(|x|(x-2)+2-k=0\)の解の個数を求めよ。
答え
\(k<1, 2<k\)のとき1個
\(k=1,2\)のとき2個
\(1<k<2\)のとき3個
まとめ
二次関数と判別式の関係についての説明でした。
二次関数の問題で判別式を使う際には「関数↔方程式」の言い換えを意識することが重要です。
二次関数の簡単な問題では意識しづらい部分ですが、しっかりと理解せずにワンランク上の問題を解こうとすると意味がわからなくなるところです。「簡単な問題だから大丈夫」と油断せずにきちんと意味を理解しましょう。