二次関数の最大値・最小値問題【高校数学で最初の山場「場合分け」】

2024年2月12日2024年4月29日

二次関数の最大値・最小値の問題は数学Ⅰの花形問題です。

ここでの最大の山場は「関数or定義域が動く際の場合分け」ですね。

たろぅ

場合分け…やってることはわかるけど、二次関数の場合分けはパターンが多いし…苦手。

という印象になりがちですが、実際には２パターンしか場合分けはありません。

この記事では、二次関数の最大値・最小値問題の基本から、場合分けのコツについて説明していきます。

二次関数の最大値・最小値問題

たろぅ

ふふーん♪

はなこ

あら、機嫌がいいわね。

たろぅ

ついに念願の「鮎型鉛筆削り機２号」を買ったんだ！『鉛筆を入れたら鮎の塩焼きのように削れる！』がキャッチフレーズ！しかも安かったんだよ！

はなこ

鉛筆派なのね…。で、いくらしたの？

たろぅ

定価が10000円なんだけど、昨日安売りしてて8000円で買ったんだよ！安くない！？

はなこ

…それ、先週セールで半額の5000円で売ってたわよ？「半額でもこんなの買うか！」って思ったけど。

たろぅ

え？ウソ？？色々信じられない。

ということで、二次関数の最大値・最小値の問題です。

二次関数は「下がる→上がる」か「上がる→下がる」という形をしているので、最大値や最小値を求めるのがやっかいです。

特にこの記事では定義域（\(x\)の範囲）が限定されている問題について話をしていきますが、

「二次関数の軸が定義域内にあるのか？」「定義域の両端の値はどちらが大きいor小さいのか？」

など、考えることが多いです。

そこでまず重要なのが「グラフをかくこと」です。グチャグチャ言葉で考えるよりもグラフをかきましょう。

せんせ

ということで、まずは二次関数の最大値・最小値の基本的な問題を解きながらグラフの重要性を確認していきましょう。
ちなみに「最大値・最小値」とは、そもそも「\(y\)の値の最大値・最小値」のことなので、グラフをかいて一番上にある部分が最大、一番下にある部分が最小となります。

例1．次の関数の最大値と最小値を求めよ。
(1) \( y = x^2-2x+2\)（\(-1 \leq x \leq 2\)）
(2) \(y = -x^2+4x-1\)（\(0 \leq x \leq 1\)）

二次関数に限らず「最大値・最小値を求めよ」と言われたらグラフをかくのが基本です。

「最大値・最小値を求める→グラフをかく」と思えば、二次関数の場合まずは平方完成、ですよね。

せんせ

他の関数の問題でも実際にグラフをかく、かかないは別問題ですが…。でも、グラフ（図）は文字情報の十数倍の情報量をもちます（クマの数学日記調べ）。面倒くさがらずに積極的にグラフをかきましょう。

ちなみに最大値・最小値問題でグラフをイメージしないのは三角関数（数学Ⅱ）…くらいですね。こちらは単位円をイメージしたほうがわかりやすいです。

（解答）

(1) \( y = x^2-2x+2=(x-1)^2+1\)（\(-1 \leq x \leq 2\)）

　よって、グラフは次のようになる。

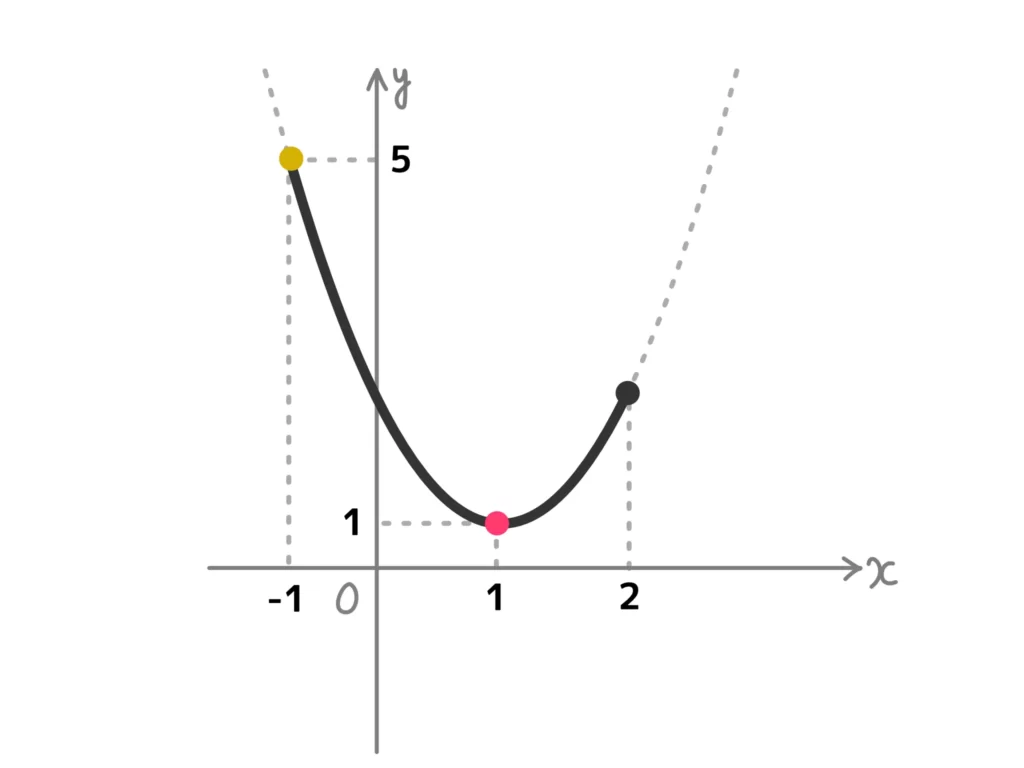
　ゆえに、最大値\(5\)（\(x=-1\)）、最小値\(1\)（\(x=1\)）…（答）

(2) \( y = -x^2+4x-1=-(x-2)^2+3\)（\(0 \leq x \leq 1\)）

　よって、グラフは次のようになる。

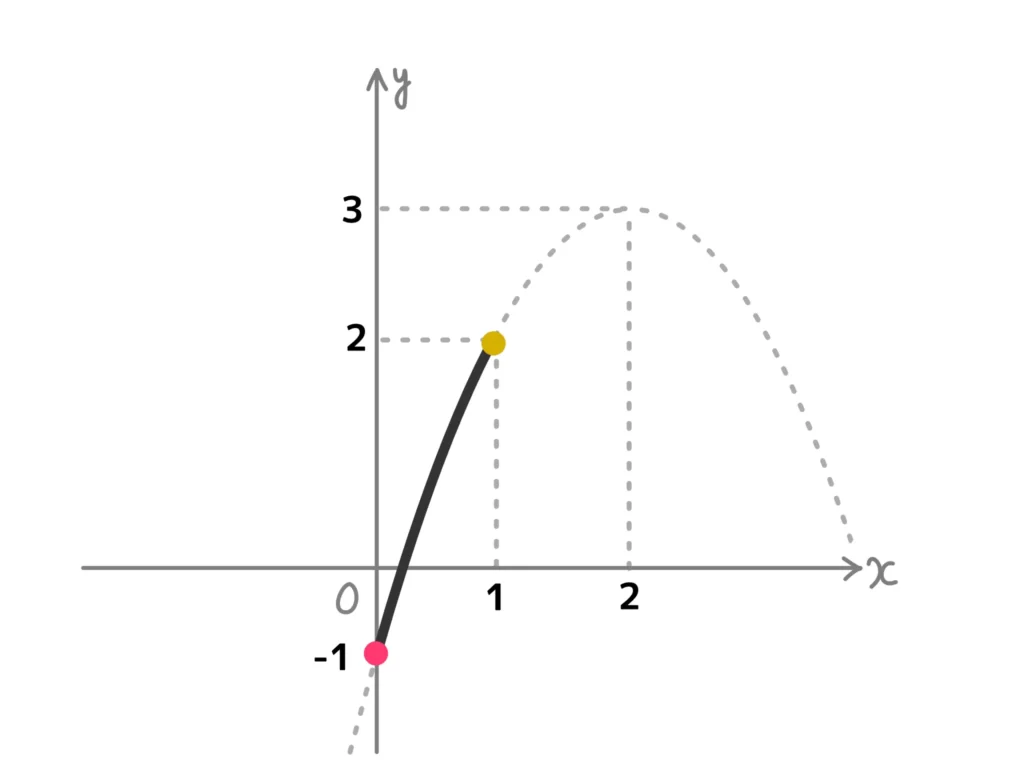
　ゆえに、最大値\(2\)（\(x=1\)）、最小値\(-1\)（\(x=0\)）…（答）

二次関数の最大値・最小値の山場「場合分け」

ここまでは基本的な二次関数の最大値・最小値問題でしたが、一番の山場は、

「関数or定義域が動くことによる場合分け」

です。

せんせ

この問題は、練習も必要です。コツはお伝えしますが、何度も練習しましょう！

場合分けでもたついていると、本当に自分が何をしているのかわからなくなるんですよね…。

練習して慣れれば見通しが立ちやすい、という側面もありますので「わからない…」と諦めずに粘り強く練習しましょう。

最大値・最小値の場合分けの基準

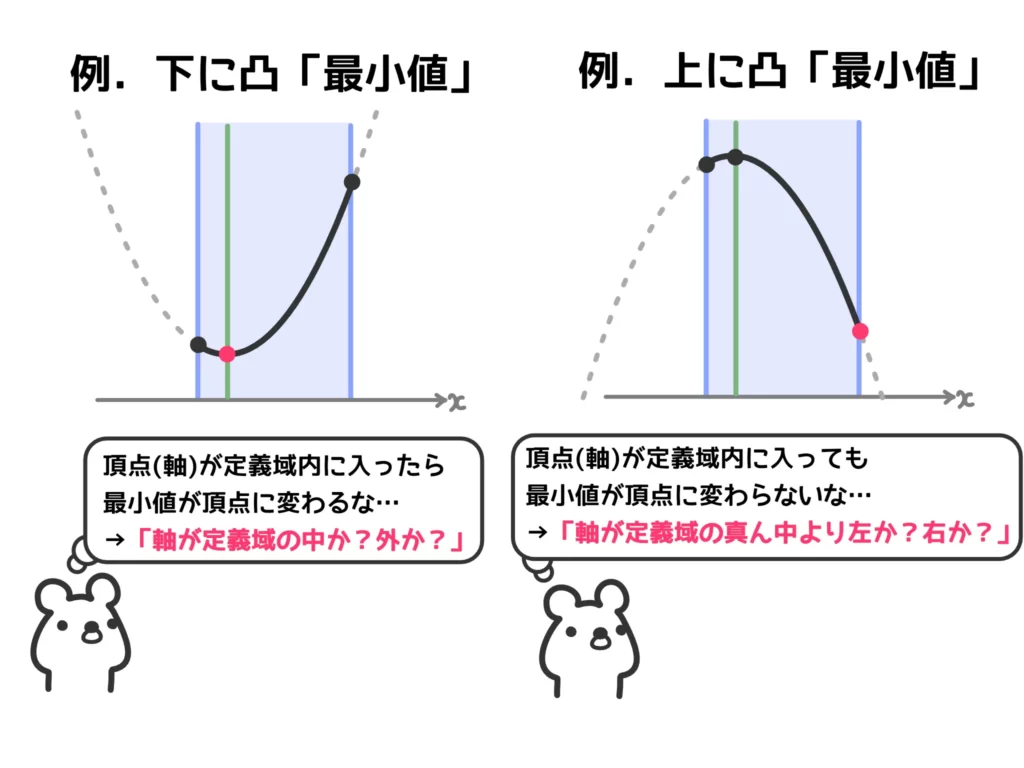
結論、「二次関数の軸が定義域の中か？外か？」「二次関数の軸が定義域の真ん中より左か？右か？」によって場合分けをします。

あとは、グラフが下に凸か？上に凸か？、最大値を求めるのか？最小値を求めるのか？、によるのですが、あまり細かくパターン分けしてもわかりにくくなります。

ですので、流れとしては

グラフが下に凸か？上に凸か？、最大値を求めるのか？最小値を求めるのか？を押さえる。
「定義域の中か？外か？」「定義域の真ん中より左か？右か？」のどちらで場合分けをするか判断する。

という感じで場合分けをしていきましょう。

せんせ

とにかく図（グラフ）をイメージするか、実際にかいて判断するのがコツです。慣れればサッと場合分けができますよ。

あとは個人的な感覚ですが、最大値を求めるのか？最小値を求めるのか？を押さえた上で、頂点の位置をイメージすると場合分けの基準が判断しやすいかな、と思います。

最大値・最小値の場合分けの問題

せんせ

それではいくつか練習してみましょう。実際に解いてみるといいかな、と思います。

例2．\(a\)を定数とする。関数\(f(x) = x^2-2ax + a\)（\(0 \leq x \leq 2\)）について、次の各問いに答えよ。
(1) 最小値を求めよ。
(2) 最大値を求めよ。

答え

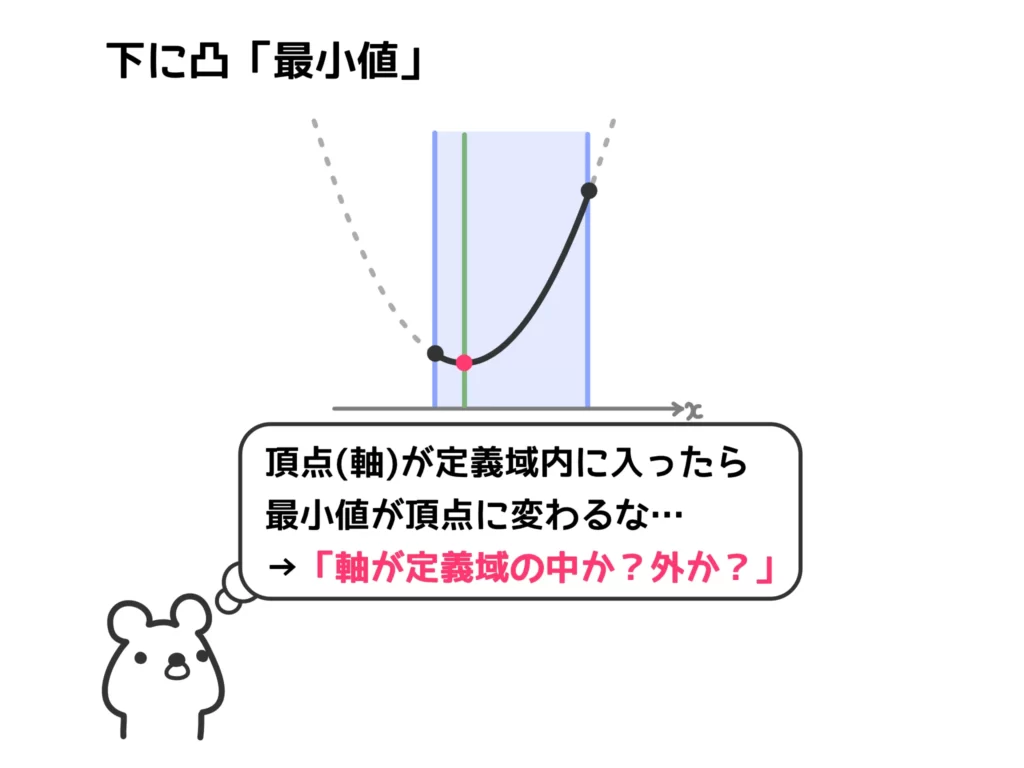
(1) 「下に凸で最小値」の問題なので、「軸が定義域の中か？外か？」で場合分けになります。

（解答）

　\(f(x) = x^2-2ax + a=(x-a)^2-a^2+a\)（\(0 \leq x \leq 2\)）

　軸：\(x = a\)

　(ⅰ) \(a < 0\)のとき

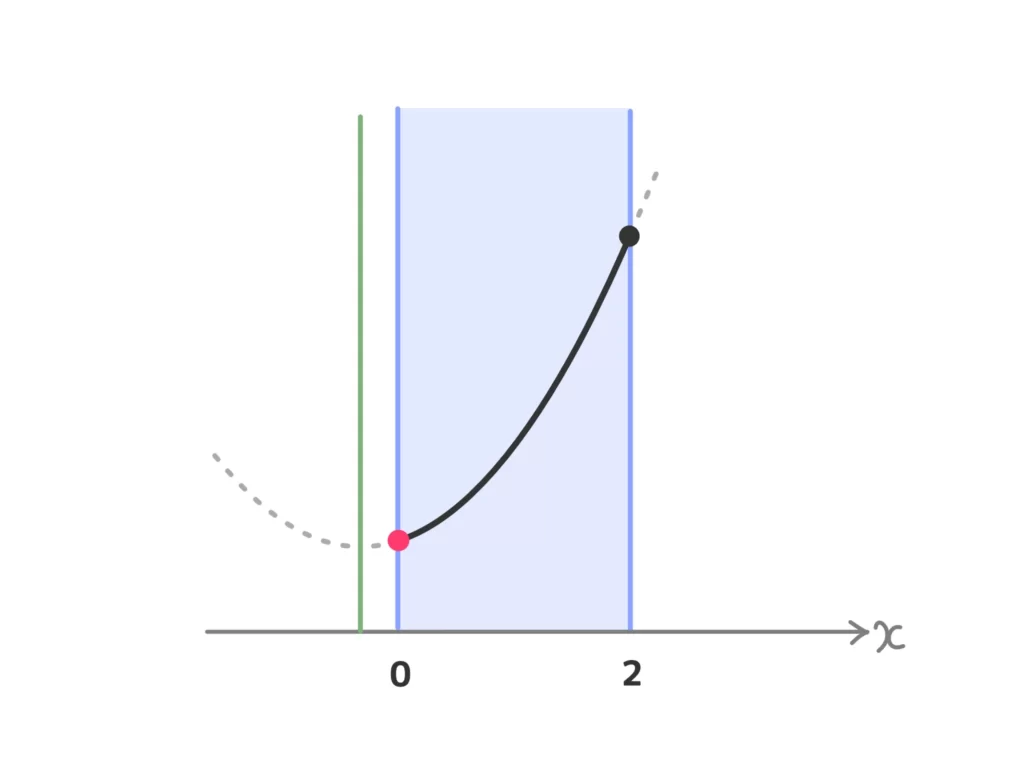
　　最小値\(f(0) = a\)

　(ⅱ) \(0 \leq a \leq 2\)のとき

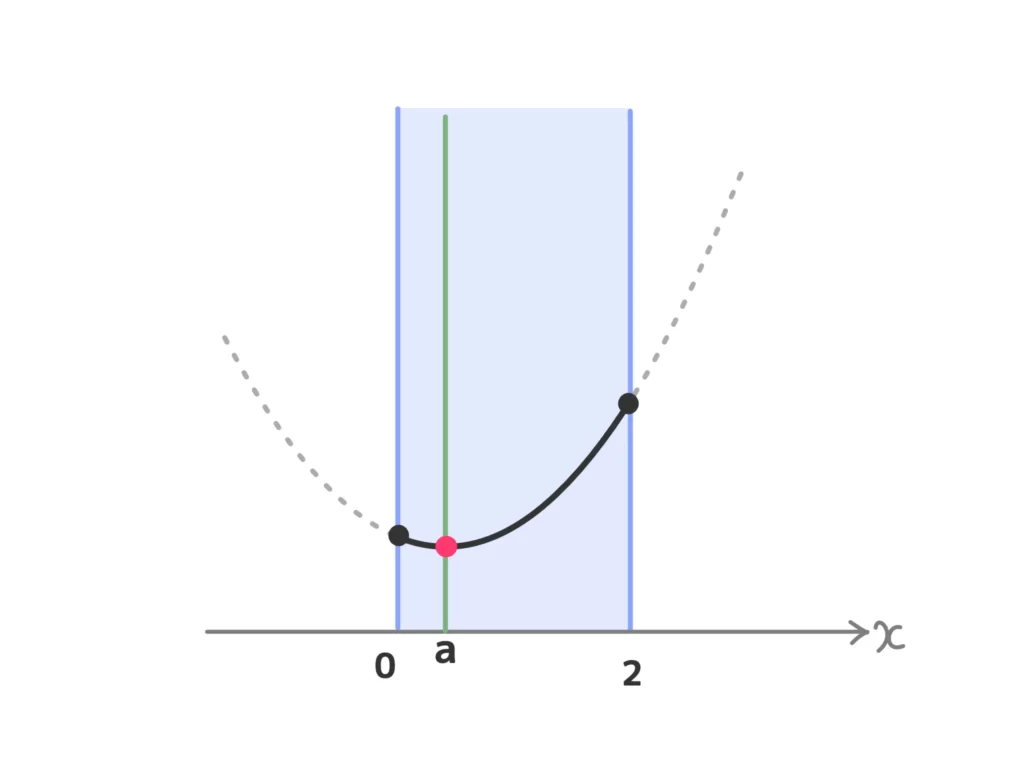
　　最小値\(f(a) = -a^2+a\)

　(ⅲ) \(2 < a\)のとき

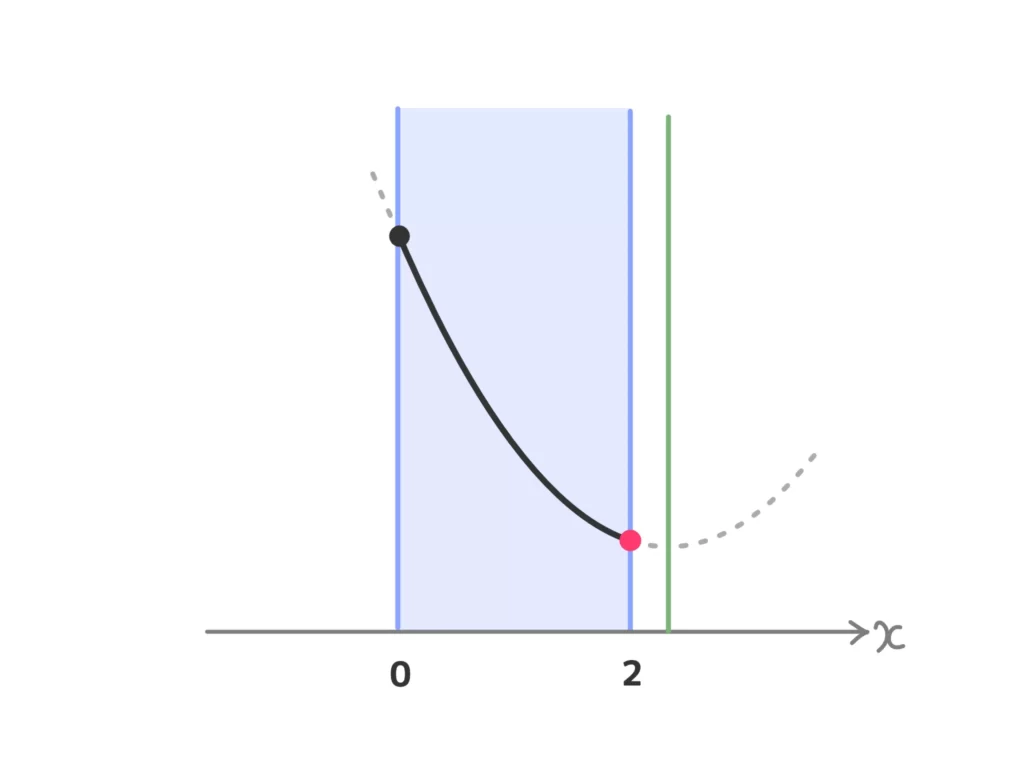
　　最小値\(f(2) = 4-3a\)

　(ⅰ)〜(ⅲ)より、最小値は
　　\(a < 0\)のとき　\(a\)（\( x = 0\) ）
　　\(0 \leq a \leq 2\)のとき　\(-a^2+a\)（\( x = a\) ）
　　\(2 < a\)のとき　\(4-3a\)（\( x = 2\) ） …（答）

【補足】
「＝」はどの場合に入れても問題はないですが、どこかには入れましょう。抜けがあったら、

せんせ

\(a=0\)のときは考えてないの？

などとツッコまれるので、落としがないようにしましょう。だからといって、

たろぅ

じゃあ全部に「＝」入れちゃえ！

もやめましょう。

なぜならば、場合分けは「重複なく」が基本的な考え方だからです。

全部に「＝」を入れても間違い…とは言えないかもしれませんが、場合分けの基本原理から外れちゃうのでやめましょう。数学A「場合の数・確率」になるとこのあたりがテキメンに現れます。

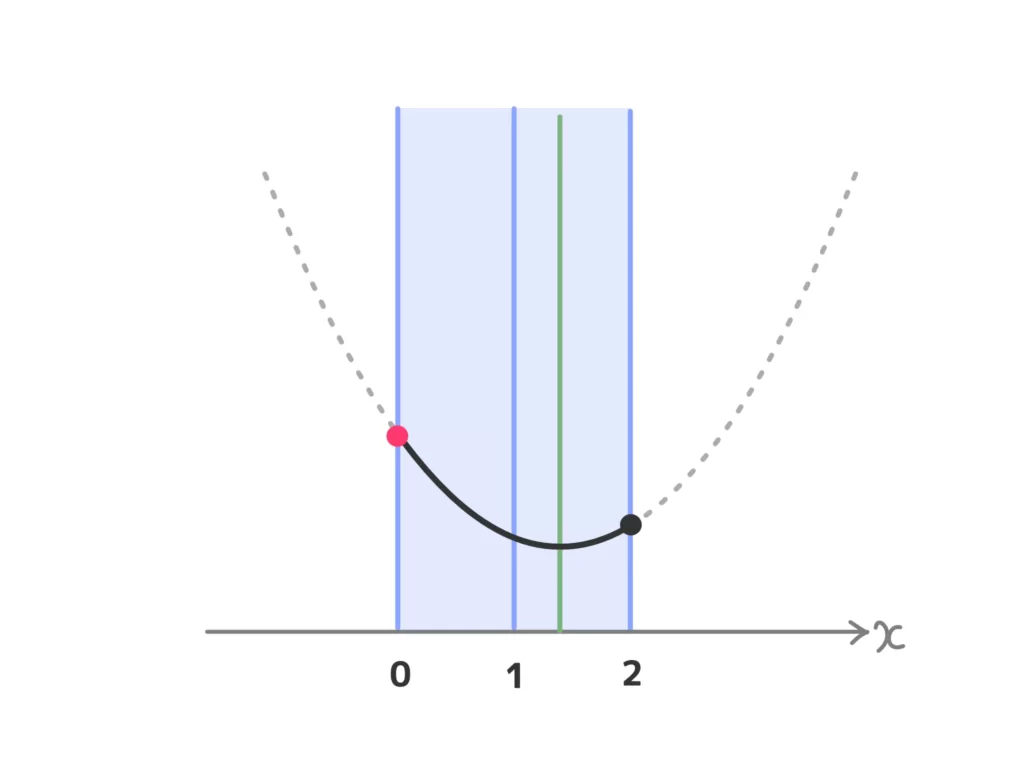
(2) 「下に凸で最大値」の問題なので、「軸が定義域の真ん中より左か？右か？」で場合分けになります。

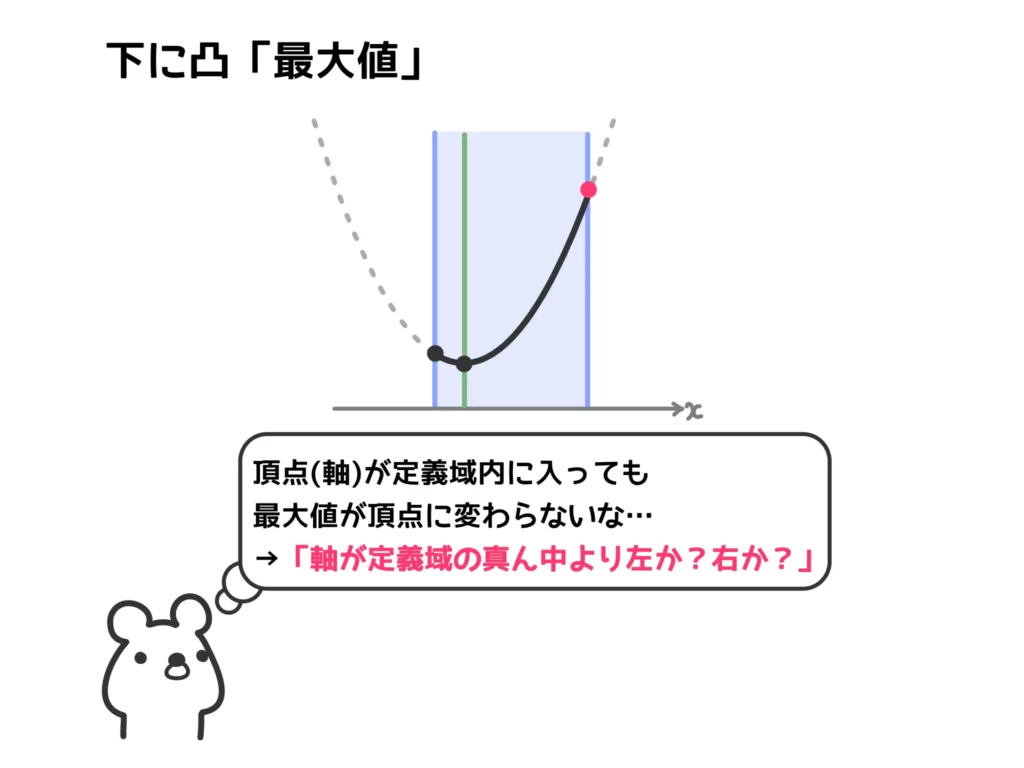
（解答）

　\(f(x) = x^2-2ax + a=(x-a)^2-a^2+a\)（\(0 \leq x \leq 2\)）

　軸：\(x = a\)

　(ⅰ) \(a < 1\)のとき

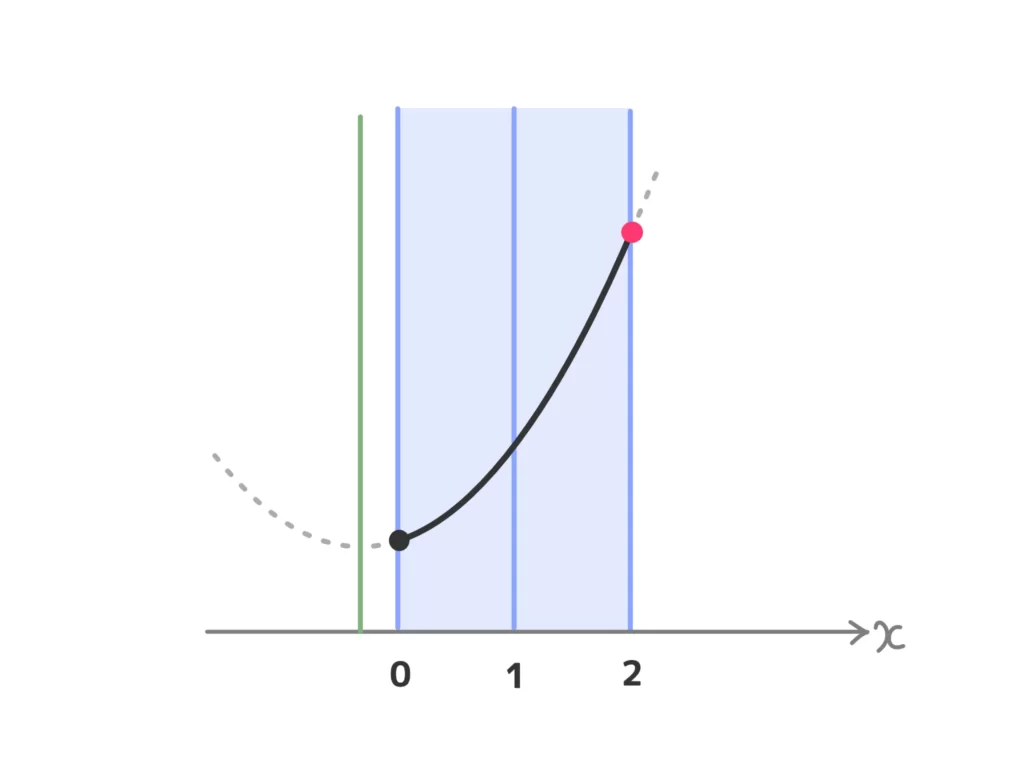
　　最大値\(f(2) = 4-3a\)

　(ⅱ) \(a = 1\)のとき

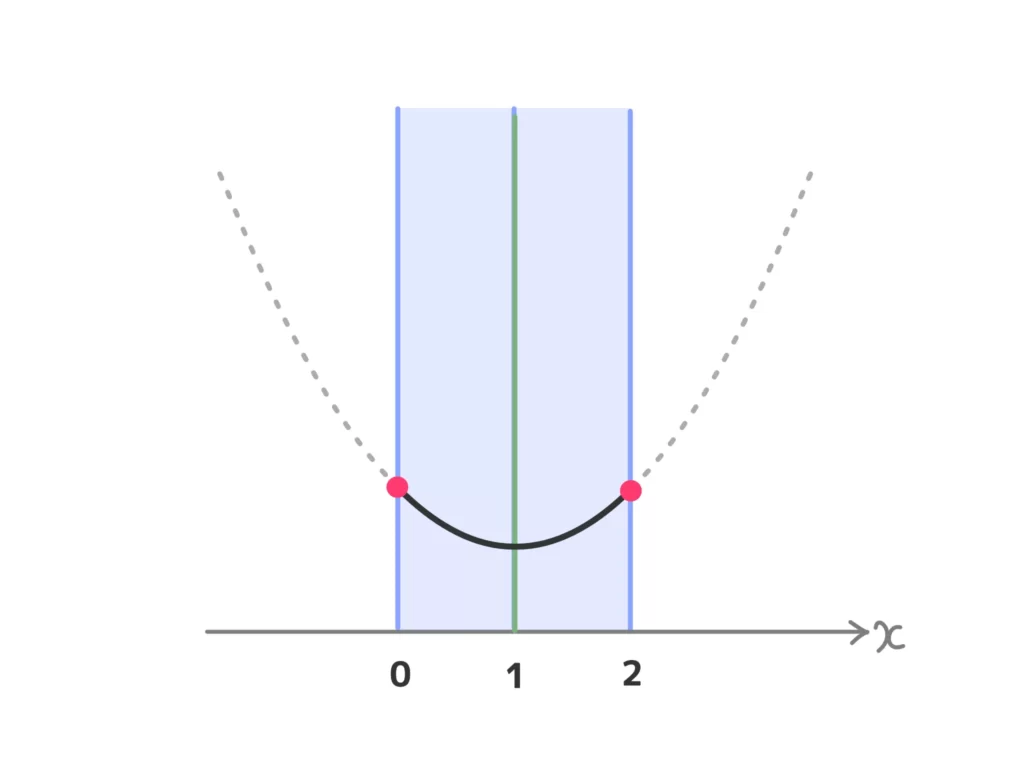
　　最大値\(f(0) = f(2) = a = 4-3a = 1\)

　(ⅲ) \(1 < a\)のとき

　　最大値\(f(0) = a\)

　(ⅰ)〜(ⅲ)より、最大値は
　　\(a < 1\)のとき　\(4-3a\)（\( x = 2\) ）
　　\(a = 1\)のとき　\(1\)（\( x = 1, 2\) ）
　　\(1 < a\)のとき　\(a\)（\( x = 1\) ） …（答）

【補足1】

場合分け（ⅱ）は\(a\)の値が確定しているので、その値を代入して具体的な（\(a\)抜きの）値を求めましょう。

【補足2】

たろぅ

（ⅱ）の場合分けを（ⅰ）か（ⅲ）に含めたらだめなの？なんか、別に問題ない気もするけど…。

という質問をよく受けますが、基本的には分けた方がいいです。問題の問われ方（最大or最小となるときの\(x\)を求める必要がない、とか）や難易度にもよりますが、基本的には分けます。

これも場合分けの原理…というか、今回の「最大値・最小値を求める判断基準」に関わるからです。

今回、そもそも場合分けをする理由が「最大となるときの\(x\)が、軸の位置によって変わるから」ですよね？

ということは、最大となるときの\(x\)が変わったときは場合分けをした方がいい、ということになります。

（ⅱ）のケースでは、（ⅰ）や（ⅲ）と違って、最大となるときの\(x\)が２ヶ所出てきます。なので、基本的には（ⅱ）を分けるべきですね。

例3．\(a\)を定数とする。関数\(f(x) = x^2-2x + 2\)（\(a \leq x \leq a+2\)）について、最小値を求めよ。

答え

今回は定義域の方が動きます。が、判断基準は揃えた方がいいです。

実際のグラフや定義域の動き方は例2とは異なりますが、「グラフの方が動くときはこんな感じで」とか「定義域が動くときはこんな感じ」というふうに分けちゃうとアタマがグチャグチャになっちゃいます。

せんせ

粛々と「軸が定義域の中か？外か？」「軸が定義域の真ん中より左か？右か？」のどちらか？を判断しましょう。

今回は「下に凸で最小値」なので「軸が定義域の中か？外か？」ですね。

（解答）

　\(f(x) = x^2-2x + 2=(x-1)^2+1\)（\(a \leq x \leq a+2\)）

　軸：\(x = 1\)

　(ⅰ) \(1 < a\)のとき

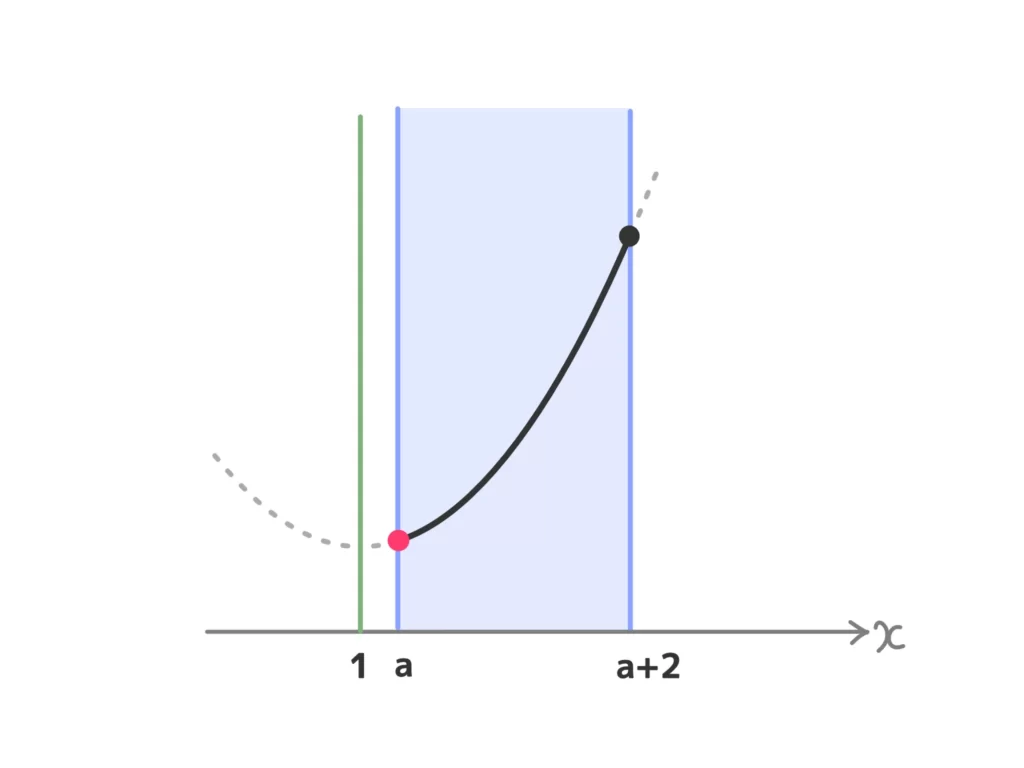
　　最小値\(f(a) = a^2-2a+2\)

　(ⅱ) \(a \leq 1 \leq a+2\)、つまり\(-1 \leq a \leq 1\)のとき

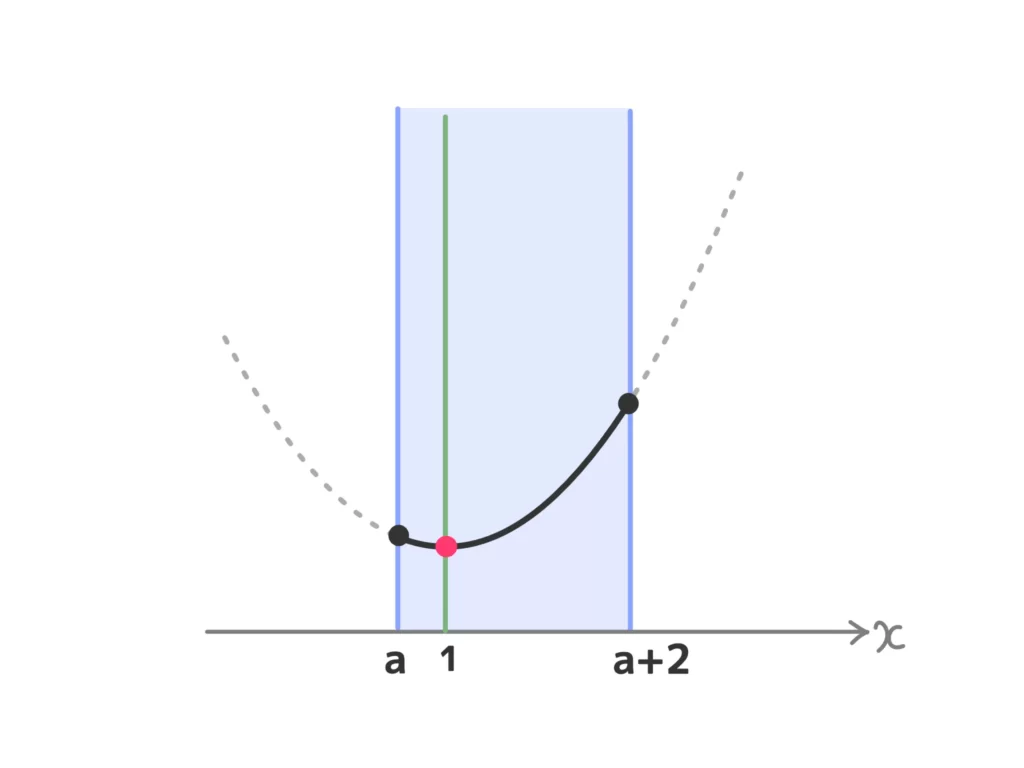
　　最小値\(f(1) = 1\)

　(ⅲ) \(a+2 < 1\)、つまり\(a<-1\)のとき

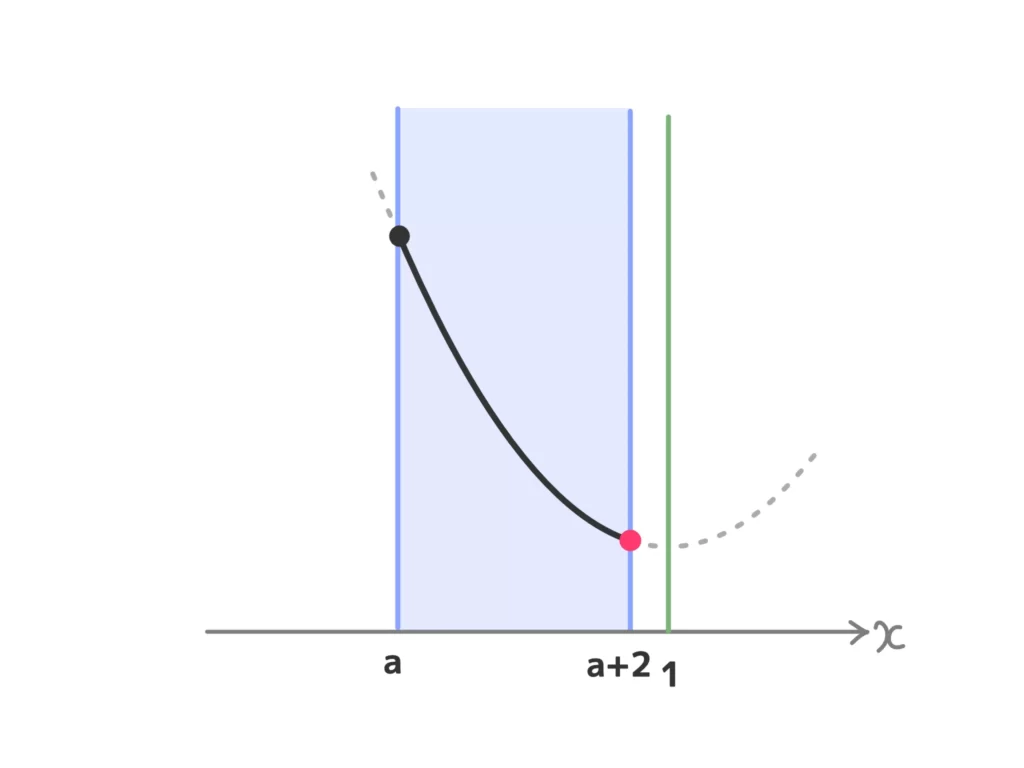
　　最小値\(f(a+2) = a^2+2a+2\)

　(ⅰ)〜(ⅲ)より、最小値は
　　\(a < -1\)のとき　\(a^2+2a+2\)（\( x = a+2\) ）
　　\(-1 \leq a \leq 1\)のとき　\(1\)（\( x = 1\) ）
　　\(1 < a\)のとき　\(a^2-2a+2\)（\( x = a\) ） …（答）

【補足】

(ⅱ)、(ⅲ)の場合分けをしたときに、\(a \leq 1 \leq a+2\)など、基準となる式は結構グチャっとなっています。

面倒ですが、「つまり\(-1 \leq a \leq 1\)のとき」のように変形して整理しましょう。

せんせ

例えばこのあと、「最小値が2となる\(a\)の値を求めよ」とかいう問題が出たりします。そのときに\(a\)の範囲を整理しておかないと、不適な\(a\)の値が出たときにハジくことができません。

ちなみに(ⅰ)の場合分けのときに式整理が必要なかったのは、たまたまです。

二次関数の最大値・最小値のチャレンジ問題

せんせ

いくつか練習問題も準備してみました！

練習問題2-6【No.19】

問．\(a\)を定数とする。関数\( f(x) = – x^2 +4ax \)（\( 0 \leq x \leq 4 \)）について、次の各問いに答えよ。
(1) 最大値を求めよ。
(2) 最小値を求めよ。

答え

(1) \(a < 0\)のとき \(0\)（\(x=0\)）
\(0 \leq a \leq 2\)のとき \( 4a^2 \)（\(x=2a\)）
\(2 < a \)のとき \( 16a-16 \)（\(x=4\)）

(2) \(a < 1\)のとき \(16a-16\)（\(x=4\)）
\(a = 1\)のとき \( 0 \)（\(x=0, 4\)）
\(1 < a \)のとき \( 0 \)（\(x=0\)）

練習問題2-7【No.20】

問．\(a\)を定数とする。関数\(f(x) = x^2-2x + 2\)（\(2a \leq x \leq 4a\)）について、次の各問いに答えよ。
(1) 最小値を求めよ。
(2) 最大値を求めよ。

答え

(1) \(\displaystyle a < \frac{1}{4} \)のとき \(16a^2-8a+2\)（\(x=4a\)）
\(\displaystyle \frac{1}{4} \leq a \leq \frac{1}{2} \)のとき \(1\)（\(x=1\)）
\(\displaystyle \frac{1}{2} < a \)のとき \(4a^2-4a+2\)（\(x=2a\)）

(2) \(\displaystyle a < \frac{1}{3} \)のとき \(4a^2-4a+2\)（\(x=2a\)）
\(\displaystyle a= \frac{1}{3} \)のとき \(\displaystyle \frac{10}{9}\)（\(\displaystyle x = \frac{2}{3} , \frac{4}{3}\)）
\(\displaystyle \frac{1}{3} < a \)のとき \(16a^2-8a+2\)（\(x=4a\)）

練習問題2-8【No.21】

問．\(a\)を定数とする。関数\(f(x) = ax^2-2 a^2 x + a^3 \)（\(-1 \leq x \leq 3\)）について、最大値を求めよ。

答え

\( a< -1\)のとき　\( a^3 +2a^2 +a\)（\(x=-1\)）
\(-1 \leq a < 0\)のとき　\( 0 \)（\(x=a\)）
\( a= 0\)のとき　最大値なし
\( 0 < a < 1\)のとき　\( a^3 -6 a^2 + 9a \)（\(x=3\)）
\( a = 1\)のとき　\( 4 \)（\(x=-1, 3\)）
\( 1 < a \)のとき　\( a^3 +2a^2 +a\)（\(x=-1\)）