PR
正弦定理と余弦定理の基本【使い分けのコツについても説明】

正弦定理と余弦定理は三角比の重要な公式です。
最近は共通テストでも若干軽視されがちな感じがしますが…やっぱり重要な公式ですね。
この記事では正弦定理と余弦定理の基本から、使い方と使い分けについて説明していきます。
 せんせ
せんせ練習問題も準備してるのでぜひご覧ください!
正弦定理と余弦定理



せんせい…正弦定理と余弦定理の使い方の違いがわかりません…。どういう状況なら正弦定理を使って、どういう状況なら余弦定理を使うんですか?



あるあるの質問ですね。じゃあ、正弦定理と余弦定理の確認からしていきますか。
ということで、正弦定理と余弦定理です。
たろうくんの質問…よく受けるんですよね。
正弦定理と余弦定理の確認から、使い方、使い分けまで丁寧に説明していきましょう。
正弦定理
三角形ABCについて(以下、\(BC=a\)、\(CA=b\)、\(AB=c\)、三角形の内角の三角比を\(\sin{A}\)…とする)、次の等式が成り立つ。
\(\displaystyle \frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R\)
ただし、\(R\)は三角形ABCの外接円の半径とする。

正弦定理の証明



図を使った証明の方がわかりやすいので、そちらをご覧ください。
(証明)
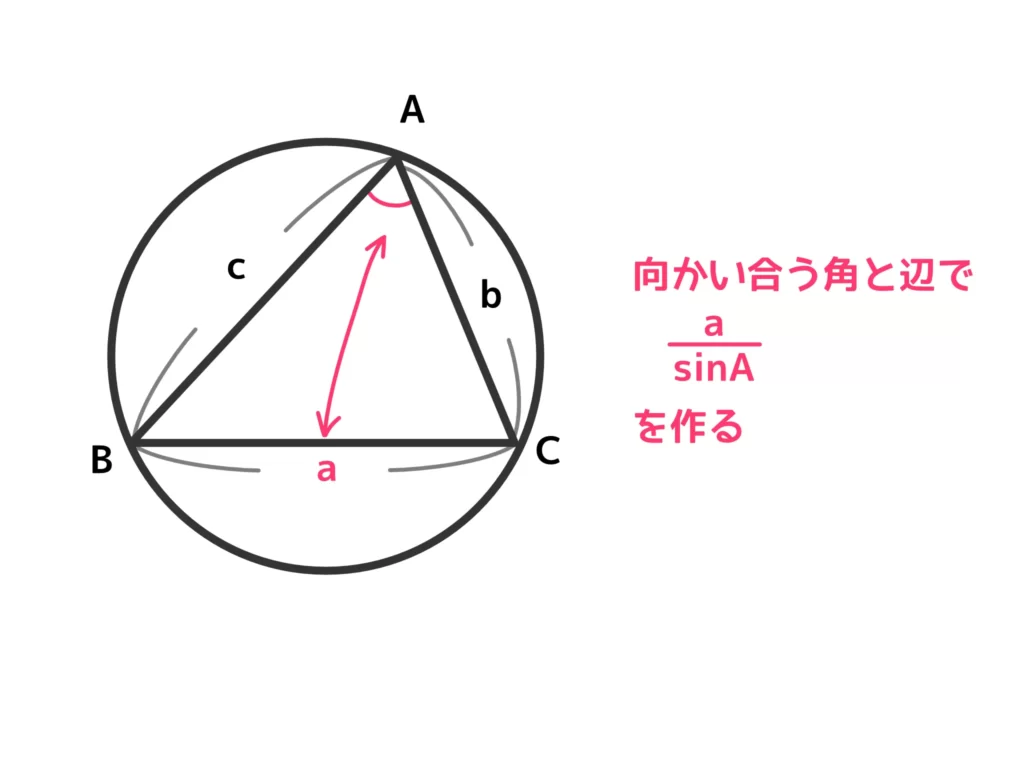
三角形と外接円を考えるとわかりやすいです。
角\(A\)と辺\(a\)について証明すればOKです。角\(B\)と辺\(b\)、角\(C\)と辺\(c\)については同様に証明できます。
(ⅰ)\(A\)が鋭角のとき
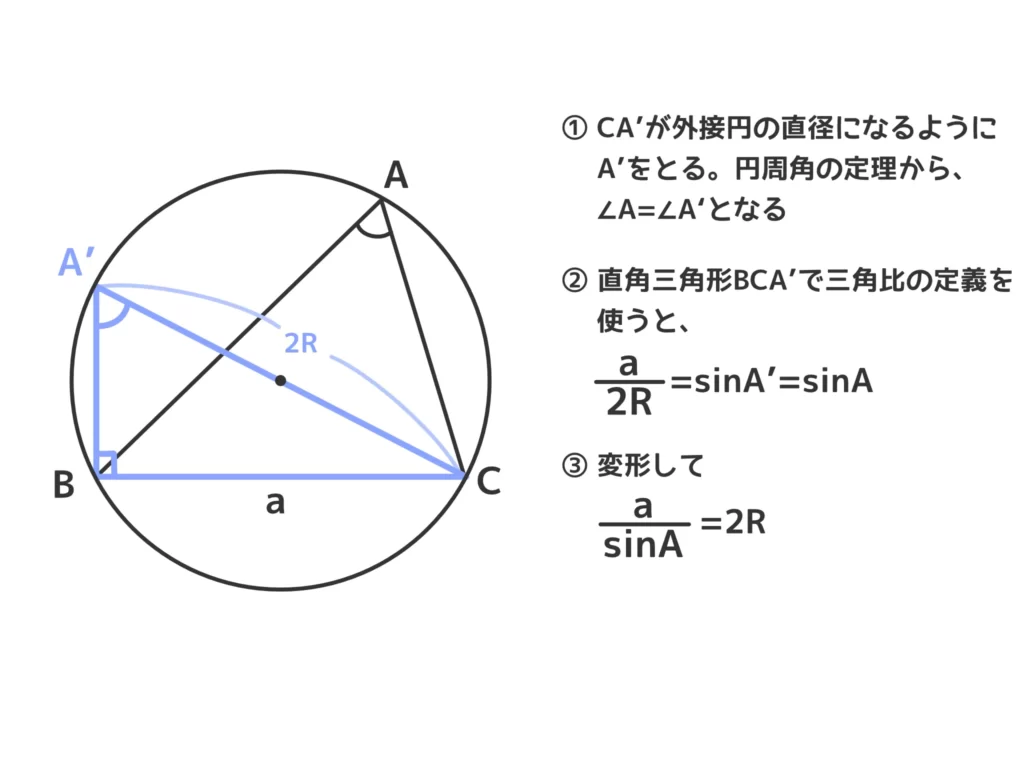

(ⅱ)\(A\)が直角のとき
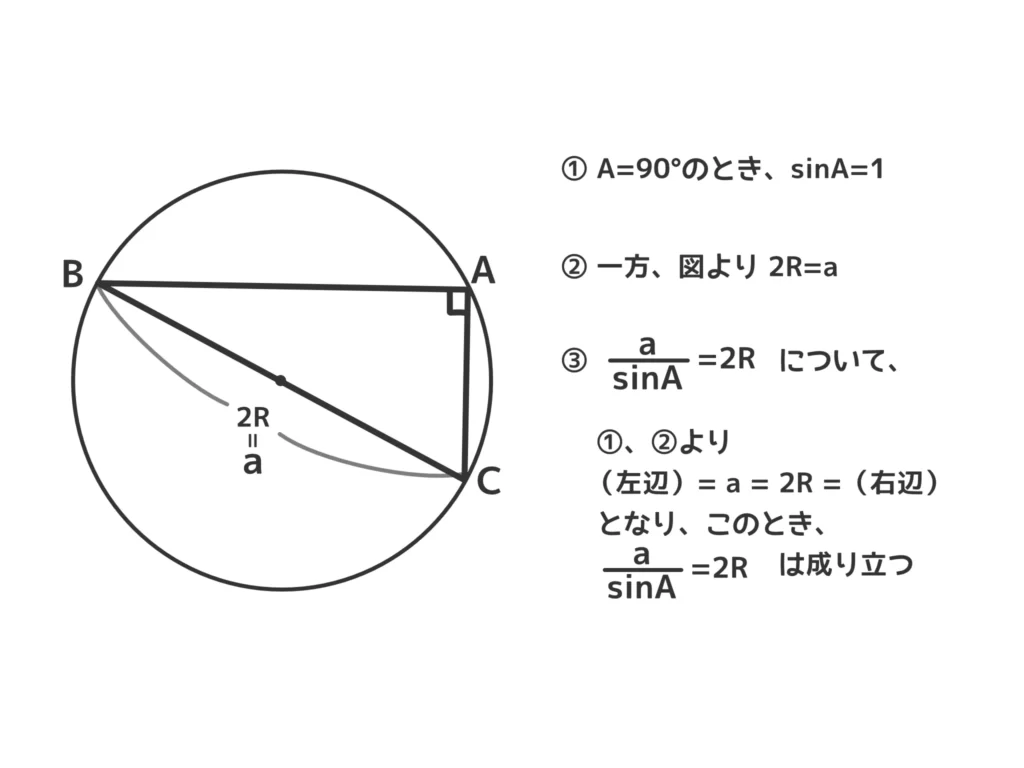

(ⅲ)\(A\)が鈍角のとき
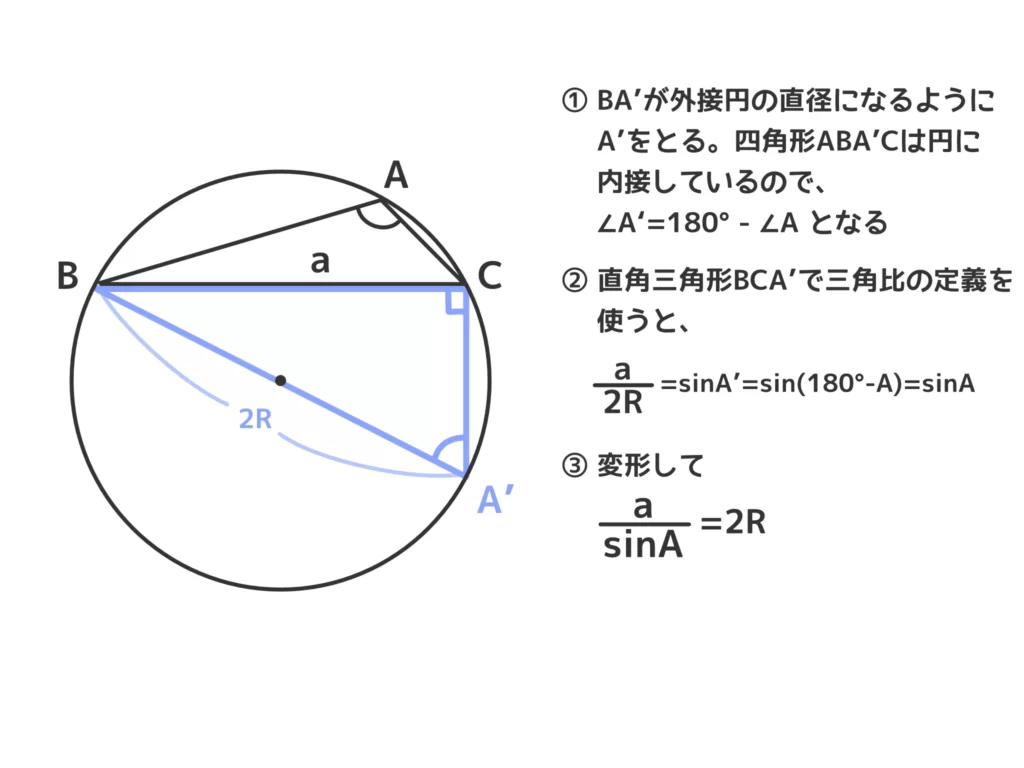

(終)
ちなみに、図形の証明をするときに、場合分けの判断が結構難しいときがあります。
今回は「外接円の直径\(2R\)について、\(\displaystyle \frac{a}{\sin{A}}=2R\)となることを示したい」というのと「最終的には直径を斜辺とした直角三角形の話にもっていく」というのが証明の軸です。
なので、「外接円を考えて、\(A\)について円周角の定理を上手く使う」ことを考えると\(A\)が鋭角なのか?直角なのか?鈍角なのか?で場合分けをすると、抜けなく・重複なく証明することができます。
余弦定理
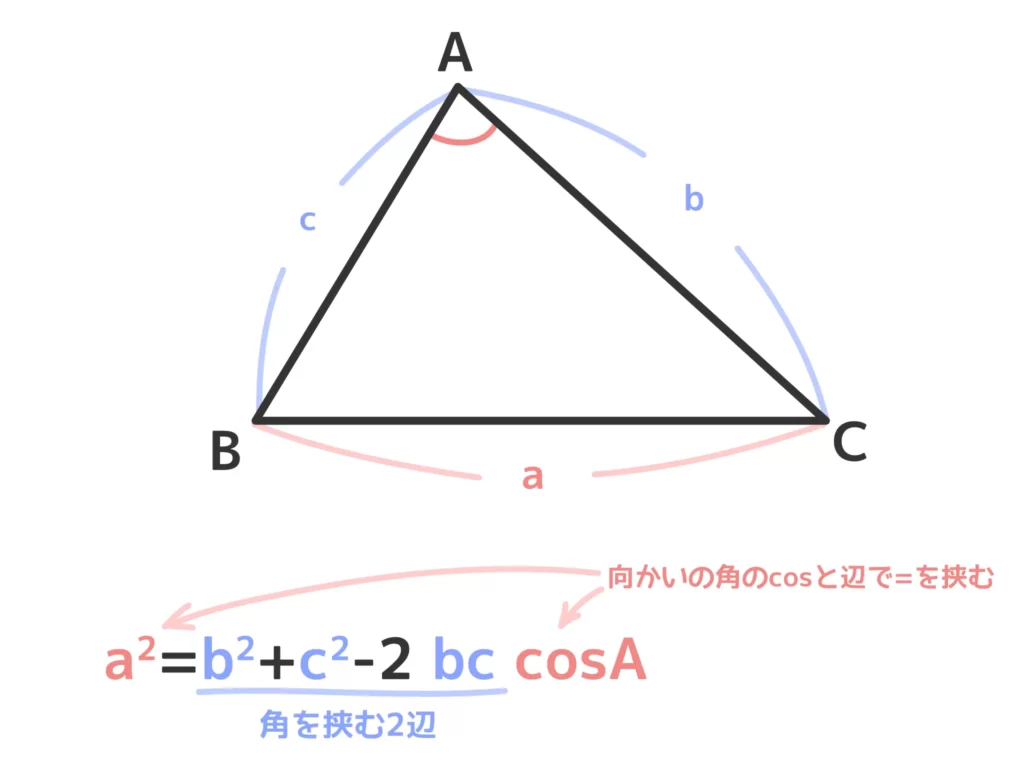
三角形ABCについて、次の等式が成り立つ。
\(a^2 = b^2 + c^2 -2bc\cos{A}\)
\(b^2 = c^2 + a^2 -2ca\cos{B}\)
\(c^2 = a^2 + b^2 -2ab\cos{C}\)

余弦定理の証明
こちらも3つの式は証明方法が同じなので、一番上の式「\(a^2 = b^2 + c^2 -2bc\cos{A}\)」を証明します。



こちらも図を使って証明していきます。
(証明)
次の図のように、左下に頂点Aを、上に頂点Bを、右下に頂点Cを置き、直線ACに向かって垂線BHを下ろします。
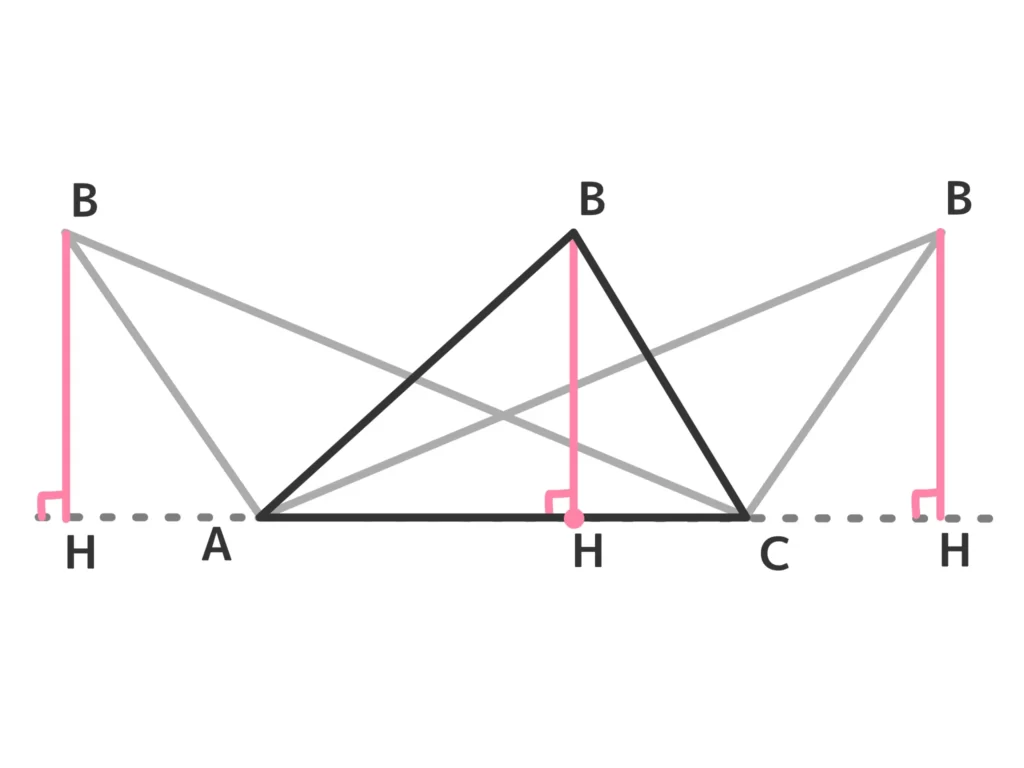

そのHが下りた先が線分AC上にあるのか?Aより左なのか?Cより右なのか?によって場合分けをします。
(ⅰ)Hが線分AC上にあるとき
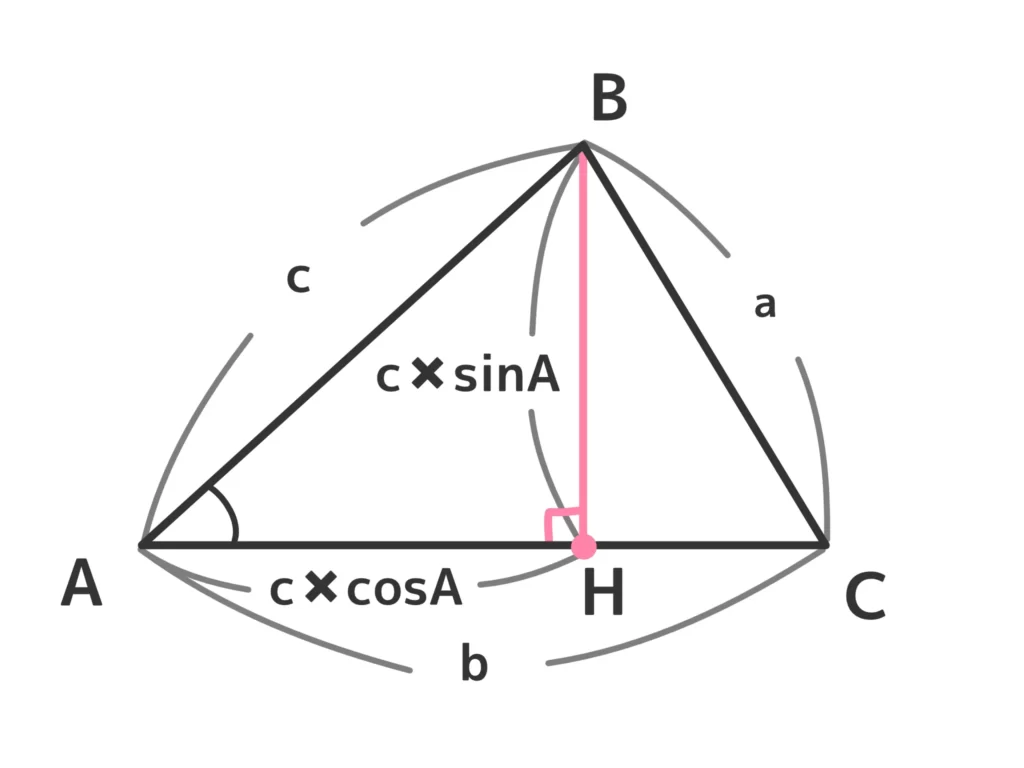

\(AH = c \cos{A}\)なので、\(CH = AC-AH = b – c \cos{A}\)。
また、\(BH = c \sin{A}\)なので、直角三角形BHCに三平方の定理を使うと、
\(BC^2 = BH^2 + CH^2\)
\(a^2 = c^2 \sin^2{A} + (b – c \cos{A})^2 \)
\(a^2 = c^2 \sin^2{A} + b^2 -2bc \cos{A} + c^2 \cos^2{A}\)
\(a^2 = c^2 (\sin^2{A}+\cos^2{A}) + b^2 -2bc \cos{A}\)
\(a^2 = b^2 + c^2 -2bc\cos{A}\)
(ⅱ)HがAより左にあるとき
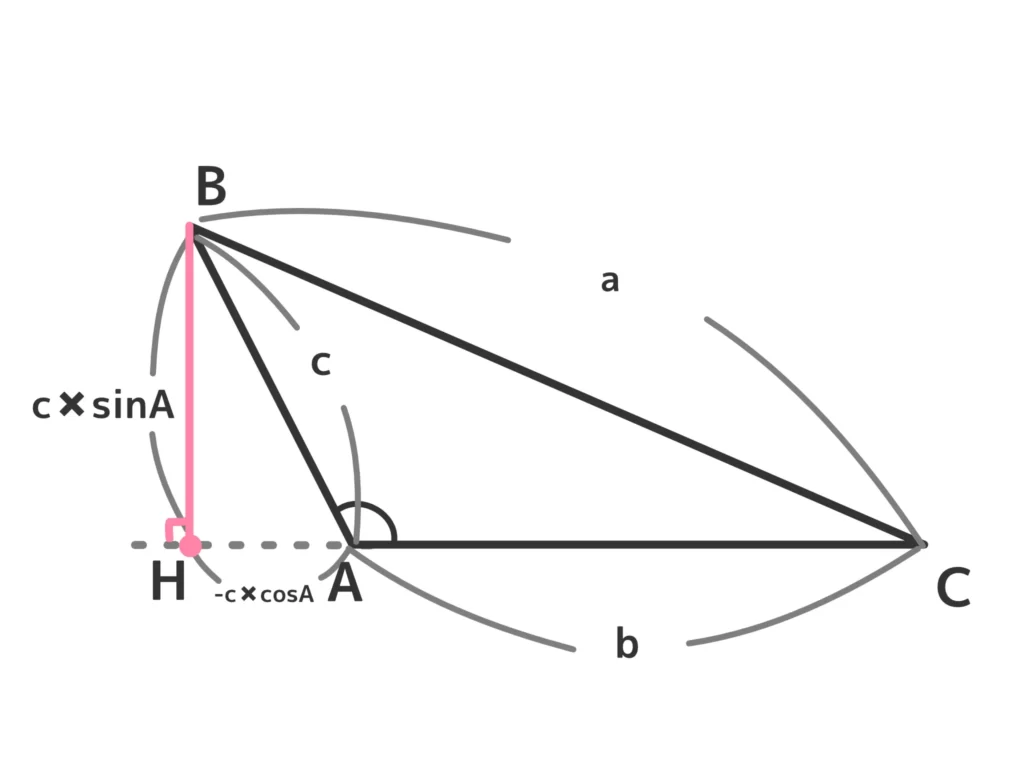

\(A\)が鈍角になるのがポイントです。
実際のAHの長さは\(AH = AB \cos{(180°-A)} = – c \cos{A}\)となります。
\(AH = – c \cos{A}\)なので、\(CH = CA + AH = b – c \cos{A}\)。
また、\(BH = c \sin{A}\)なので、直角三角形BHCに三平方の定理を使うと、(ⅰ)と同様の計算になり\(a^2 = b^2 + c^2 -2bc\cos{A}\)
(ⅲ)HがCより右にあるとき
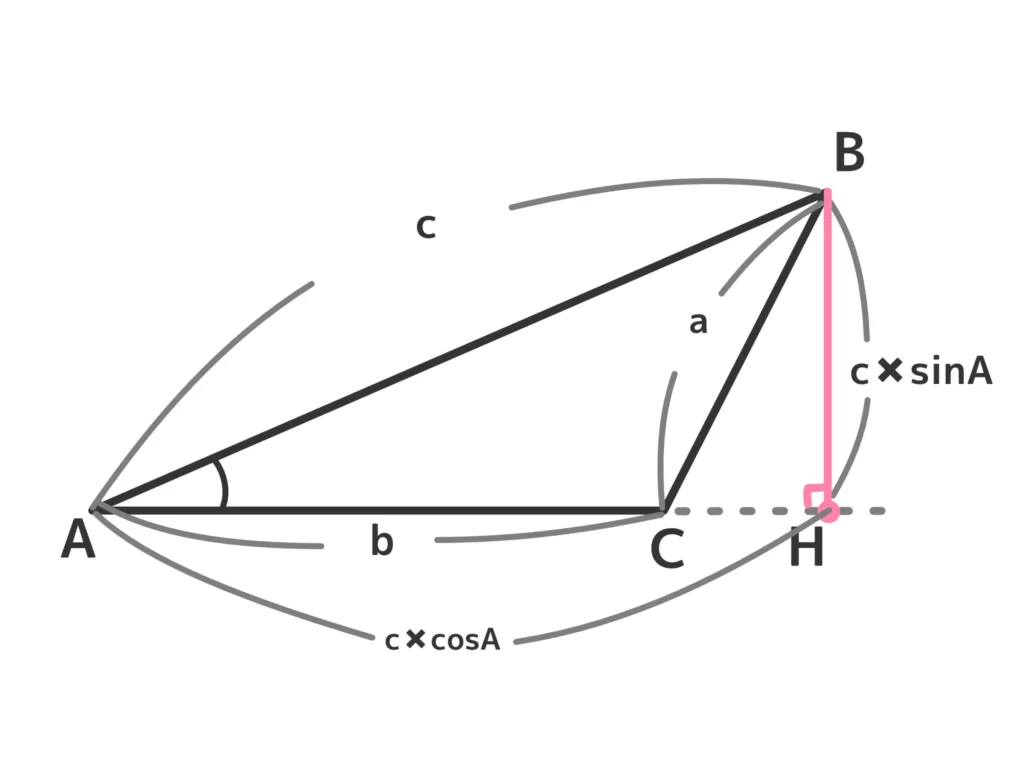

\(AH = c \cos{A}\)なので、\(CH = AH – AC = c \cos{A} – b\)。
また、\(BH = c \sin{A}\)なので、直角三角形BHCに三平方の定理を使うと、
\(BC^2 = BH^2 + CH^2\)
\(a^2 = c^2 \sin^2{A} + (c \cos{A}-b)^2 \)
\(a^2 = c^2 \sin^2{A} + c^2 \cos^2{A} -2bc \cos{A}+ b^2\)
\(a^2 = b^2 + c^2 -2bc\cos{A}\)
(終)
こちらも場合分けの判断がわかりにくいですね…。特に教科書などは「\(A\)が鋭角、\(A\)が鈍角、\(C\)が鈍角」など、基準がわかりにくい書き方をしているものもあります。



実際はHがどこに落ちるか?によって場合分けをしています。これによって、AHの長さの表し方と、CHの長さの求め方が変わるからです。
正弦定理と余弦定理の使い方
正弦定理の使い方
正弦定理は「①三角形の外接円の半径を求めたいときor外接円の半径がわかっているとき」か「②三角形の内角の\(\sin\)と向かい合う辺が1組わかっている+その他の角の\(\sin\)or辺が1つわかっている」ときに使えます。
①の状況、つまり「外接円の半径」がカラんでいるときに使うことが多いです。②は条件としてはかなり厳しいので使いにくいですが、内角の\(\sin\)と向かい合う辺が1組わかっているときには使える可能性アリです。



「外接円の半径」がカラんできたら十中八九、正弦定理の出番ですね。
余弦定理の使い方
余弦定理は「2辺とその間の角の\(cos\)」がわかっていれば使えます。が、実際のところは2辺とどこかの角の\(cos\)がわかっていれば、わかっていない辺を\(x\)と置いて立式することで\(x\)を求めることができます。
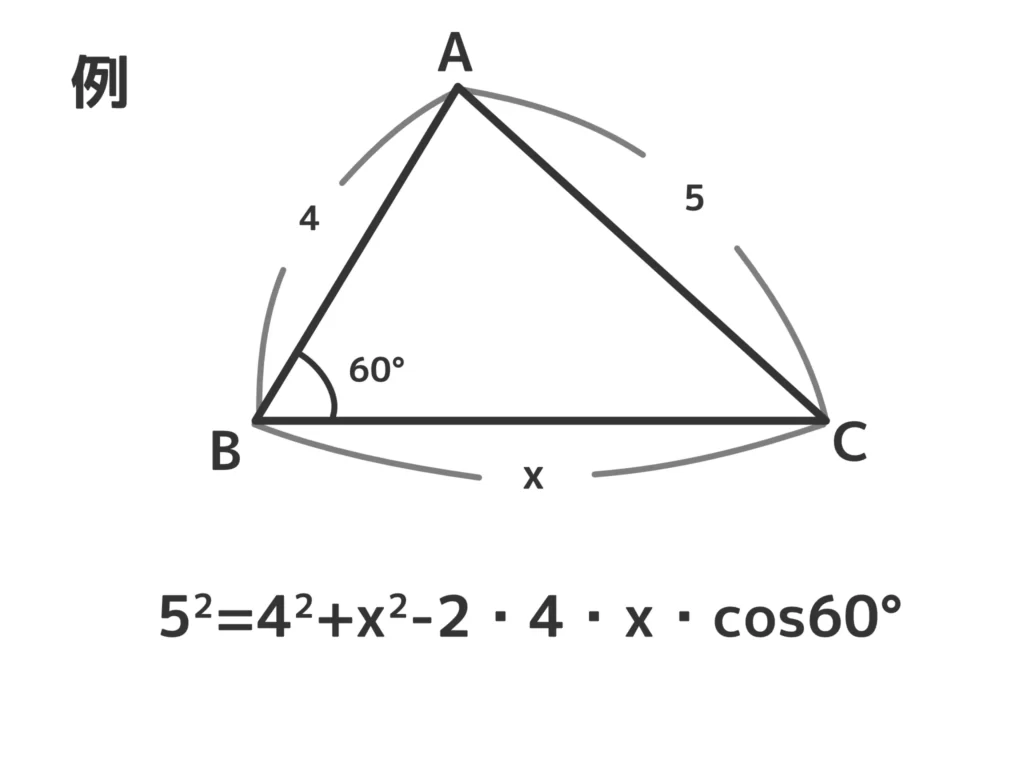

あとは、3辺がわかっているときに\(cos\)の値や、そこから角を求めることができます。
余弦定理から\(\cos\)を求める
\(\displaystyle \cos{A} = \frac{b^2 + c^2 -a^2}{2bc}\)
\(\displaystyle \cos{B} = \frac{c^2 + a^2 -b^2}{2ca}\)
\(\displaystyle \cos{C} = \frac{a^2 + b^2 -c^2}{2ab}\)



公式の形は正弦定理よりも複雑ですが、その分応用は効きやすいです。
余弦定理は3種類ありますが、実質1つだけ覚えておけばOKです。
「角と向かいの辺」と「2辺とその間の角」の位置関係を覚えて使いましょう。


正弦定理と余弦定理の使い分け
正弦定理の方が形がシンプルな分、「角の\(sin\)と向かい合う辺が1組わかっていないといけない」という強めの制約があるので、まずはここを判断基準にしましょう。
逆にいうと、
「角の\(sin\)か\(cos\)、or角の値」と「向かい合う辺」が1組わかっている状況では正弦定理を使うチャンスです。
あとは、特別な状況でない限り、外接円の半径がカラむ公式は正弦定理くらいしかないので「外接円の半径」ときたら正弦定理を使うのではないか?と思いましょう。
それ以外では余弦定理を使うことの方が多いです。先ほど説明したように、「2辺」と「角」の位置関係の制約が無いのが大きいですね。



外接円が問題で出てきても、「四角形に外接する円」だったら余弦定理を使いますしね…。
大事なのは、どの角や辺の情報があるかを丁寧に拾っていくことですね。
正弦定理と余弦定理の練習問題
練習問題を用意しましたが…シンプルですが意外とヘビーです。



「この図形はありえるのか?」という疑いの目をもって解きましょう。
問.三角形ABCにおいて、\(AB=7\)、\(A=45°\)、\(\displaystyle \cos{B} = \frac{3}{5}\)であるとする。このとき、次の各問いに答えよ。
(1) \(B\)は60°より大きいか?小さいか?評価せよ。また、45°より大きいか?小さいか?評価せよ。
(2) 三角形ABCは鋭角三角形か?鈍角三角形か?理由をつけて答えよ。
(3) BCの長さとACの長さを求めよ。
答え
(1) \(B\)は60°より小さく、45°より大きい。
(2) 鋭角三角形
(3) \(BC=5\)、\(AC=4\sqrt{2}\)
正弦定理と余弦定理のまとめ
正弦定理と余弦定理の使い方についてでした。
- 正弦定理は「向かい合う角と辺の組が必要」「外接円の半径カラみ」で使うことが多い
- 余弦定理は公式の形は複雑だが結構使いやすい。「角と向かいの辺+2辺とその間の角」の位置関係を意識すると立式しやすい。
という特徴があるので、正弦定理・余弦定理を使うときには参考にしてみて下さい。