積分とは！？わかりやすく説明【これを知ってから教科書を読もう】

2024年3月16日

積分は高校数学の花形分野です。

ですが、授業で積分を習うときには、

「積分は微分の逆だよ〜」

といきなり言われるので、

たろぅ

…ん？で？

となりがちです。

この記事では、積分の本質的なイメージを掴みながら微分と積分の繋がりについて説明していきます。

積分とは

授業（教科書）では

せんせ

積分は微分の逆の計算だよ〜
→不定積分っていうのがあるよ〜

せんせ

→定積分ってのもあって、こんな計算するよ〜

せんせ

→定積分は関数で囲まれた部分の面積を求めるときに役に立つよ〜

という流れで習います。まぁ、これはこれで「積分は微分の逆演算だからとりあえず計算してみよう」→「実は面積なんか求められて便利なんだよ」という感じで、スタートではお茶を濁しながら、でも比較的スムーズに積分計算とテクニックを習得できます。

ですが、少なくとも歴史的には「定積分で関数のグラフに囲まれた面積を求める」ことから積分計算が出発しているので、本来は「定積分」の考え方が先なんですよね…。

定積分を先に学習する必要はないですが、この本来の積分が生まれた背景を知っておくと、「微分の逆演算である不定積分の必要性」がわかってとっつきやすくなります。

せんせ

教科書の流れだと微分から積分が生まれたような感じがしますが、実際には別々に生まれて結びついた、というイメージが正しいですね。

ということで、定積分のイメージをざっくりと説明すると、「インテグラルの中身の関数の値を細かく動かしながら足していく」という感じです。

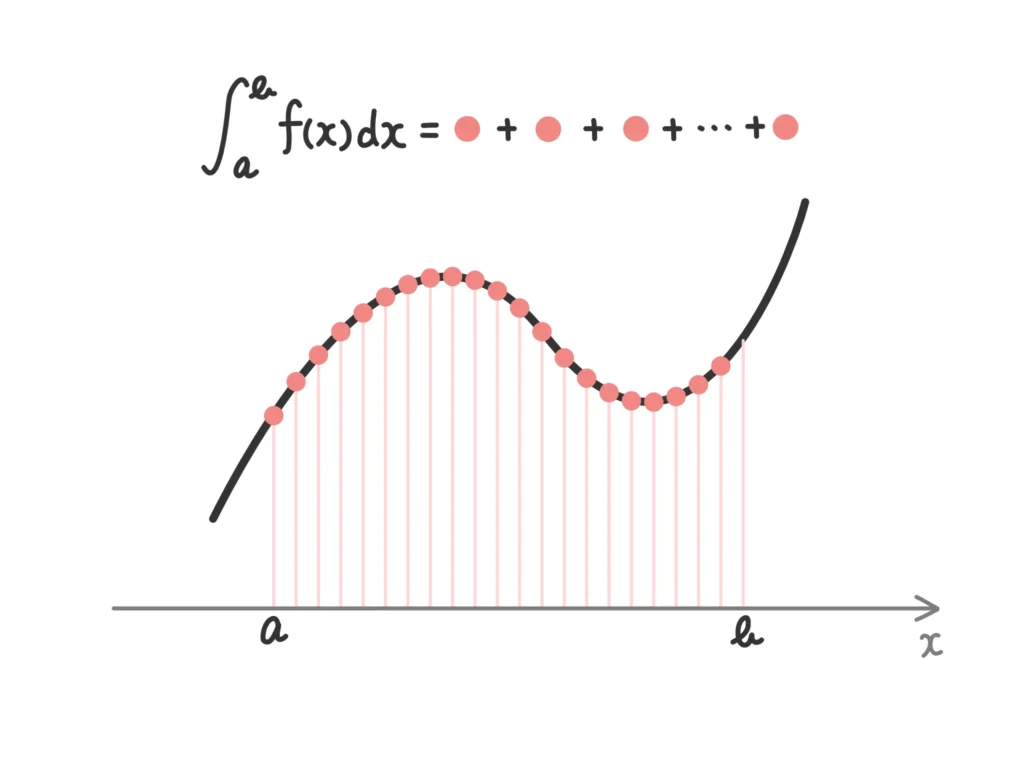
このイメージは、積分の計算をしたり、面積や体積を正しく求めるために意識しておくことをオススメします。

せんせ

今回、色々な本とかを読み漁りましたが、積分が生まれた背景は結構複雑ですね…汗
ですが、やはり「関数で囲まれた部分の面積を求めるために、関数の値を細かく足し合わせている（正確には関数の値を高さとした細い長方形を足し合わせている）」というイメージがわかりやすく、しっくりくると思います。

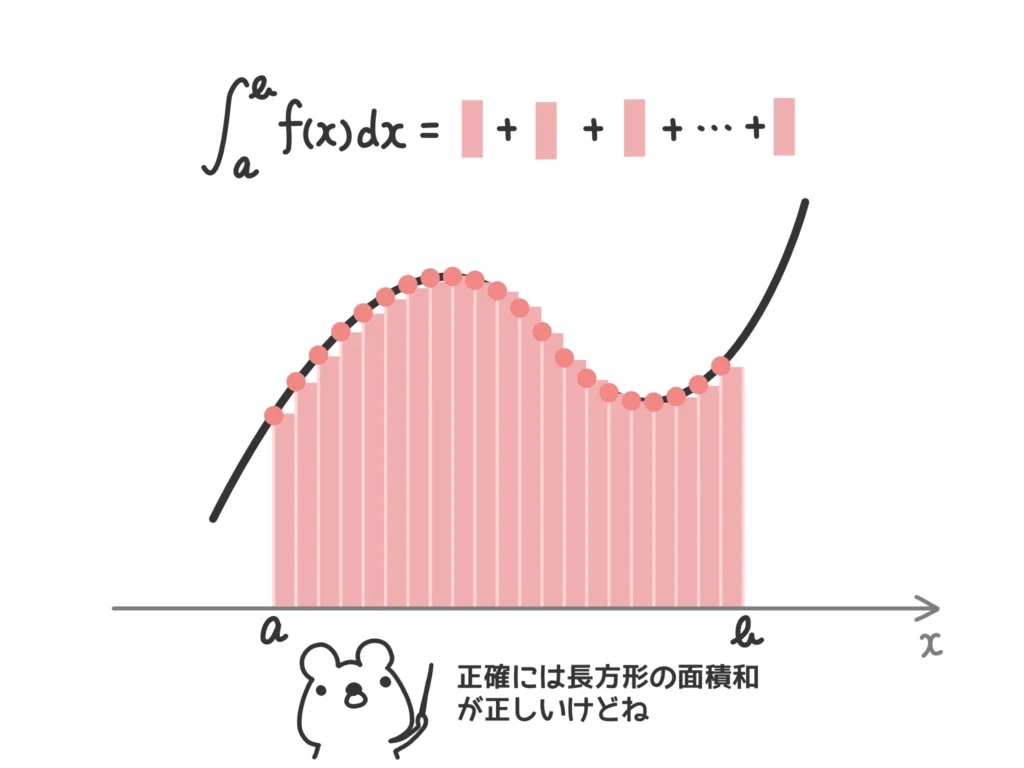
ただし、もう一つ重要なポイントとしては「積分は中身の関数の値を細かく動かしながら足していくだけであり、ただ、そういう計算をしているにすぎない」というのも意識しておきましょう。

つまり、例えば中身の関数の値がー（マイナス）であれば、それを足し合わせた結果は当然ー（マイナス）になります。

せんせ

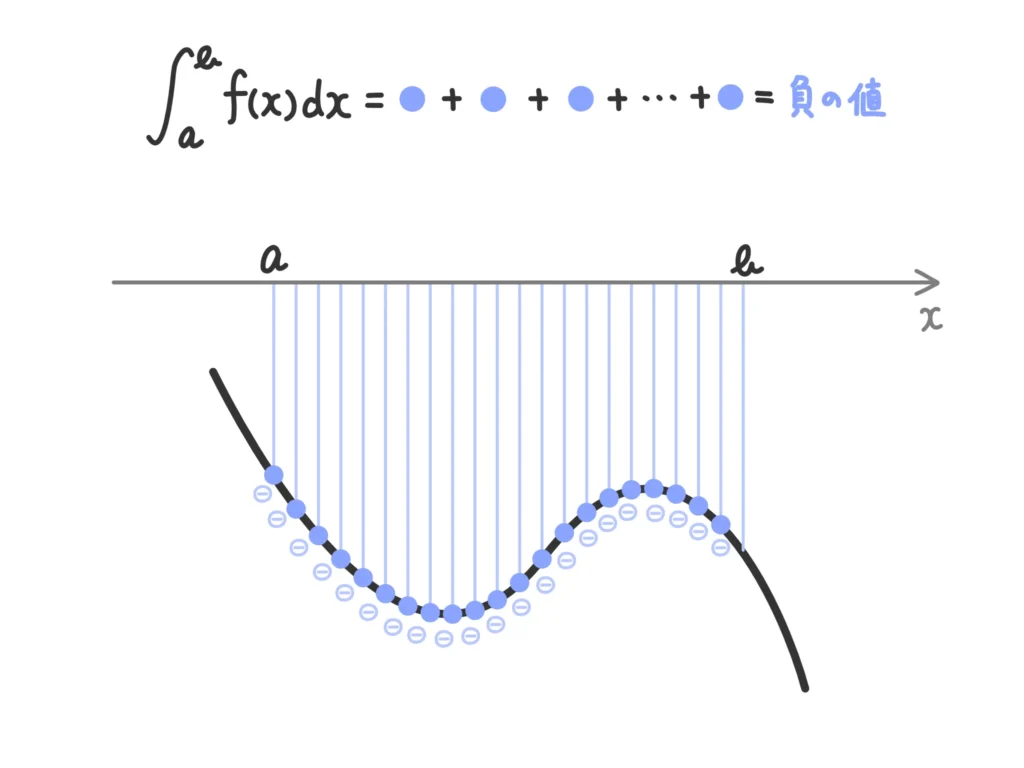
定積分の計算は、あくまで機械的に中身の関数の値を細かく足し合わせる、という計算するだけです。そこに「面積」の意味を持たせたいなら、中身の関数を上手く調整する必要があります。

ちなみに、定積分を計算するために、そもそも「積分という計算方法」を知っていないと計算できません。

ですので、積分を体系立てて学習する際には当然不定積分を先に学習します。不定積分に関しては、やはり「微分の逆演算」というイメージでいいかな…と思います。

このあたりの「ニワトリが先か？卵が先か？」みたいなところが、微積の分野にはありますね…。

積分と微分を結びつける

ということで、そもそも積分は「微分の逆の計算」どころか、関係ないところから出発しています。

ただし、どちらも「無限に小さい変化量」という考えは共通しており、

無限に小さい変化量で関数の振る舞いを調べる → 微分

無限に小さい変化量を使って関数で囲まれた面積を求める → 積分

となります。

ですが、これらは「逆演算」という結びつきがあることがわかってきます。（歴史的に）

せんせ

それでは
「積分した関数を微分したら元の関数に戻る」
ことを証明して、積分が微分の逆の計算であることを示してみましょう！

ちなみに、「積分は微分の逆演算」というのは積分の最初に教わることなので、それでOKな人は読み飛ばしてくれても大丈夫です。

あくまで積分の本質・出発点は「インテグラルの中身の関数の値を細かく動かしながら足していく」というイメージなので、それが微分とどう結びついていくのか？が知りたい方はぜひ読んでみて下さい。

せんせ

ちなみに、数学Ⅲで習う平均値の定理まで使うので、結構ヘビーです。が、雰囲気は伝わると思います。

まずは準備です。

準備① 主役の関数と、ゴールを確認しましょう。

主役の関数を\(\displaystyle F(x) = \int_{a}^{x}f(t)dt\)とします。また、今回のゴールは「この\(F(x)\)を定義にしたがって微分したら\(f(x)\)になる」のを示すことです。

たろぅ

\(F(x)\)は「\(f(t)\)を積分し（て変数を\(x\)とし）たもの」だから、それを微分して元に戻ることが示せたなら、積分と微分は逆の計算、ということになりますね…。

式でかくと、「\(\displaystyle F'(x) = \frac{d}{dx}\int_{a}^{x}f(t)dt = f(x)\)となる」ことを示せばOKです。積分で一番最初に習う「積分は微分の逆演算」を示すのに、式の書き方自体も、積分をしばらく習わなければ出てこない…という矛盾。

せんせ

結果自体は、数学IIの積分を習ってしばらくすれば出てきます。が、今回はこれを定義に従って微分していきます！

準備② 定理を１つ確認します。

この証明をするためには定理が１つ必要になります。

積分型の平均値の定理

区間\( [a, b]\)で連続な関数\(f(x)\)について、

\(\displaystyle \int_{a}^{b}f(x)dx = (b-a)f(c)\)

となる\(c\)が\(a < x < b\)のどこかに存在する。

せんせ

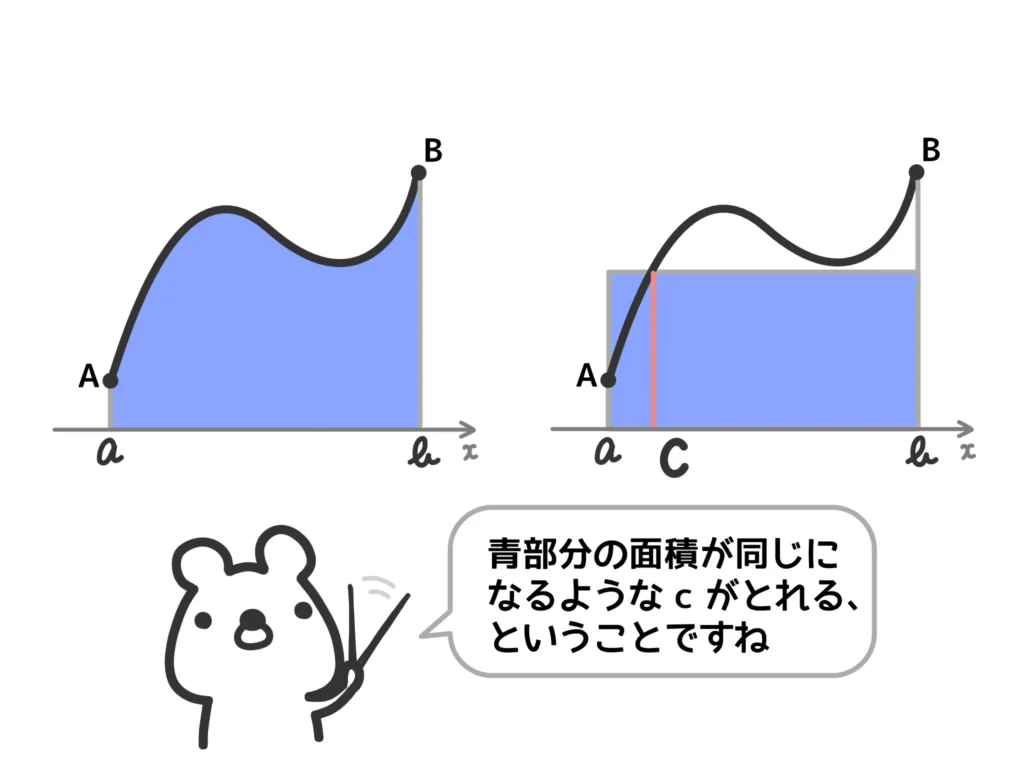
この定理の証明についてはコチラの記事をご覧ください！

これで準備は整いました！

せんせ

では実際に証明してみましょう！

（証明）

いきなりですが、積分型の平均値の定理をちょっとだけ加工します。

\(\displaystyle \int_{a}^{b}f(x)dx = (b-a)f(c)\)の\(c\)を

\(c = a +(b-a)\theta \)（\(0 < \theta < 1\)）と表現し直します。

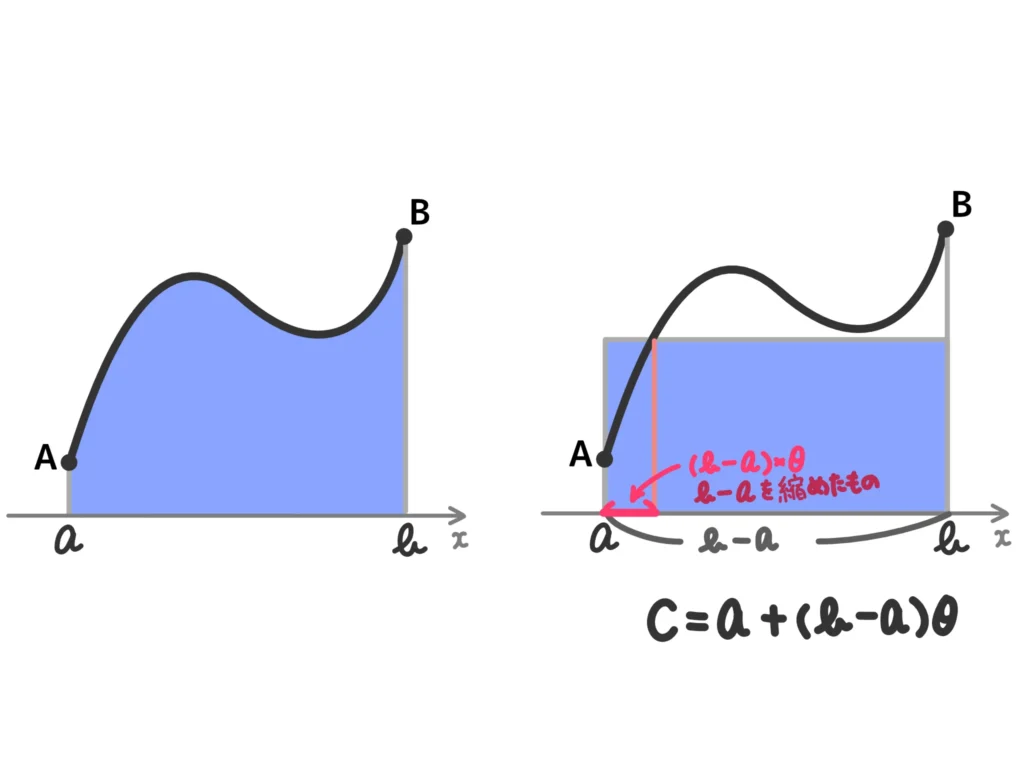
よって、積分型の平均値の定理は

\(\displaystyle \int_{a}^{b}f(x)dx = (b-a) f ( a + (b-a)\theta ) \)…(※)

となる\(\theta\)が\(0 < \theta < 1\)に存在する。という式に加工されました。

せんせ

形は複雑になっちゃいましたが、これが後で効いてきます！

ここからが本番です。\(F(x)\)を定義に従って微分していきます。

\(\displaystyle F(x+h) – F(x) = \int_{a}^{x+h}f(t)dt – \int_{a}^{x}f(t)dt\)
\(\displaystyle \quad = \int_{a}^{x}f(t)dt + \int_{x}^{x+h}f(t)dt – \int_{a}^{x}f(t)dt\)
\(\displaystyle F(x+h) – F(x) = \int_{x}^{x+h}f(t)dt\)…(※※)

ここで、加工した平均値の定理(※)の\(a\)、\(b\)を\(a \rightarrow x\)、\(b \rightarrow x+h\)、
\(x \rightarrow t \)とする（\(x\)は文字が被るのと、(※※)に形を寄せるため）と、

\(\displaystyle \int_{x}^{x+h}f(t)dt = (x+h-x)f(x + (x+h-x)\theta )\)
\(\displaystyle \quad = hf(x +h\theta )\)

という形に、\(\theta\)を使って変形できます。

よって、(※※)は

\(\displaystyle F(x+h) – F(x) = \int_{x}^{x+h}f(t)dt= hf(x +h\theta )\)

と表すことができます。

\(\displaystyle \frac{F(x+h) – F(x)}{h} = \frac{hf(x +h\theta )}{h} = f(x +h\theta )\)なので、

\(\displaystyle F'(x) = \lim_{h \to 0}\frac{F(x+h) – F(x)}{h} = \lim_{h \to 0}f(x +h\theta ) = f(x)\)

以上より、\(\displaystyle F'(x) = \frac{d}{dx}\int_{a}^{x}f(t)dt = f(x)\)。

せんせ

ちょっと複雑ですが、実際には積分型の平均値の定理を「こんなのがあるんだ…」と飲み込めれば、あとはそこまで難しくないはずです！平均値の定理は結構こういう本質的な証明に使ったりします。

積分のまとめ

積分とは？というお話でした。

結果、「積分は微分の逆の計算」というのを証明するために、微積分に相当慣れていないとわからない話をしてしまいました…スイマセン汗。

積分を初めて勉強する人は積分（定積分）のイメージを先に押さえておくことをオススメします。

一通り積分を勉強してみて、「で？結局積分って？」という疑問がある人や「微分と積分のつながりをもう少し詳しく知りたい」という人もゆっくり読みながら理解してもらえたらな、と思います。

せんせ

とにかく積分は「中身の関数の値を細かく動かしながら足し合わせる」というイメージを持っておいて下さい！