偶関数・奇関数とグラフの対称性の調べ方のコツ【重要性と本質的な意味も】

2024年3月16日

偶関数・奇関数は数学IIの「三角関数」のところで習います。（もしかしたら習わずに飛ばしちゃうかもしれません。）

簡単に説明すると、関数が表すグラフが対称になる、という話なのですが…これがなかなか重要なお話なんです。

この記事では、偶関数・奇関数とはなにか？という基本的な部分から、偶関数・奇関数の調べ方と調べることの重要性、偶関数・奇関数の性質まで、わかりやすく説明していきます。

偶関数・奇関数とは？

たろぅ

うーむ…。

はなこ

あら？どうしたの？

たろぅ

いや、ウチの庭師がさ…。

はなこ

…庭師？あんたの家、庭師がいるの？

たろぅ

え？いるだろ？庭師？

はなこ

…うん、そうね。で？その庭師が？

たろぅ

ウチの庭をさ、西洋風の庭園にしちゃったのよ…。俺はずっと日本風がいいって言ってたのに…。なんか、あのキッチリした感じが落ち着かないんだよね…。

はなこ

…（西洋風の庭園、ってもしかしてコイツんち、めっちゃ広いんじゃ…。）

ということで、偶関数・奇関数です。

偶関数・奇関数は関数の対称性の話で、\(y\)軸対称なものを偶関数、原点対称なものを奇関数といいます。

西洋風の庭園も左右対称でキッチリしたものが多いですね。偶関数です。（←？）

庭はともかく、数学的には対称性というのは意外と重要な性質です。グラフはもちろん、式も対称性による性質があったりします。

偶関数・奇関数

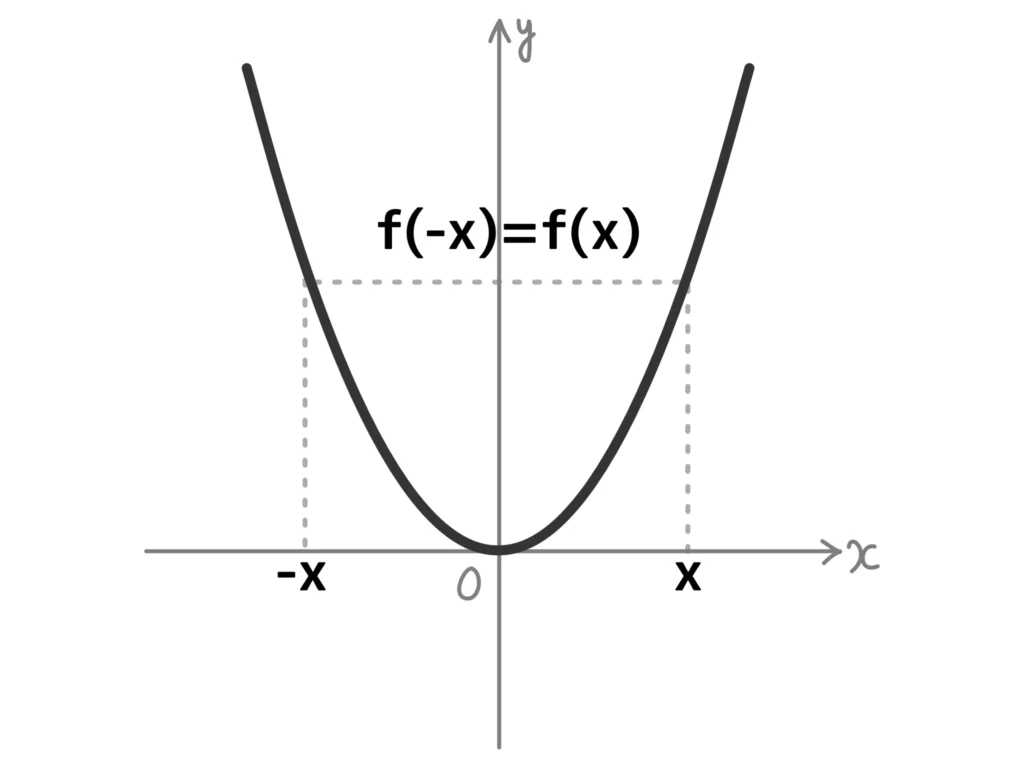
偶関数：\(y\)軸に対して対称なグラフをもつ関数。\(f(-x) = f(x)\)となる。

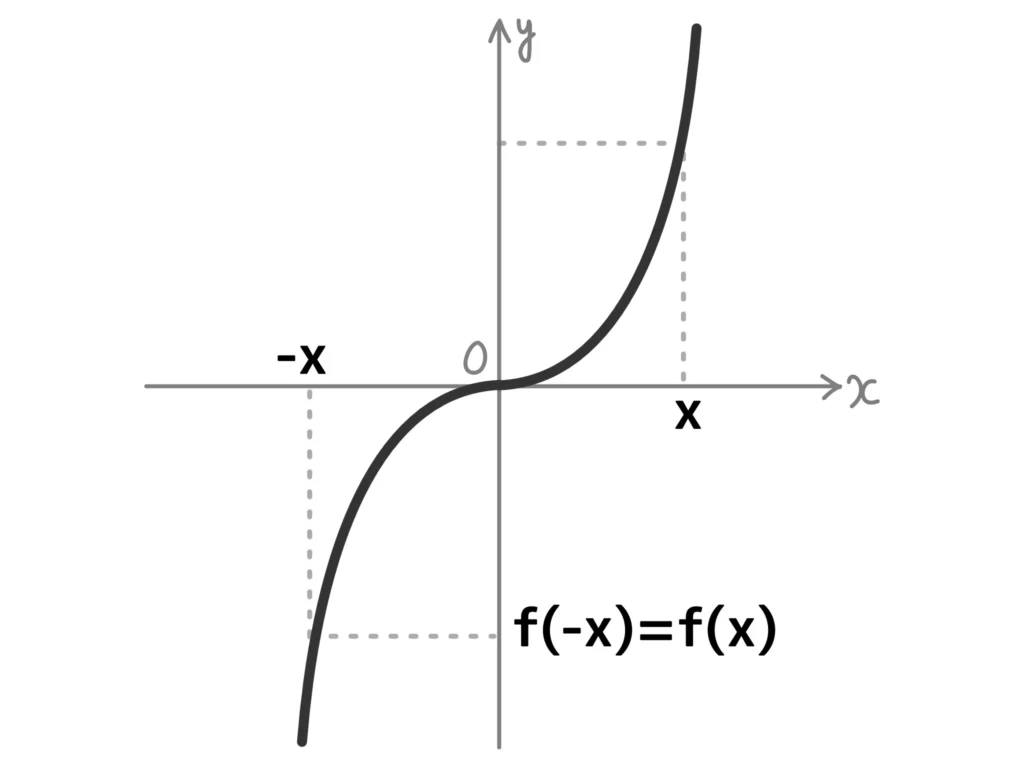
奇関数：原点に対して対称なグラフをもつ関数。\(f(-x) = -f(x)\)となる。

たろぅ

んー…まぁ「対称な」ってとこはわかりますけど、「\(f(-x) = f(x)\)」とか「\(f(-x) = -f(x)\)」ってのがよく意味がわかんないんですけど…。

せんせ

そうですね。詳しく説明する前になぜ対称性が重要か？を軽く説明しておきましょう。

グラフの対称性を調べる意味

結論から言うと、計算量を減らすことができます。しかも半端じゃなく減らせます。４割〜９割引です。

一番最初に恩恵を受けるのは数学IIの積分です。本当は一番最初に出てくるのは三角関数なのですが、正直ここでは全く偶関数・奇関数の恩恵は受けません。

せんせ

例えばこんな積分があったとしましょう。

例．\(\displaystyle \int_{-1}^1 x^2 dx\)、\(\displaystyle \int_{-1}^1 x^3 dx\)

ここで、\(x^2\)は偶関数、\(x^3\)は奇関数であることに注意して下さい。

詳細はコチラの記事で説明していますが、次の図を参考にすると計算がかなりラクになります。

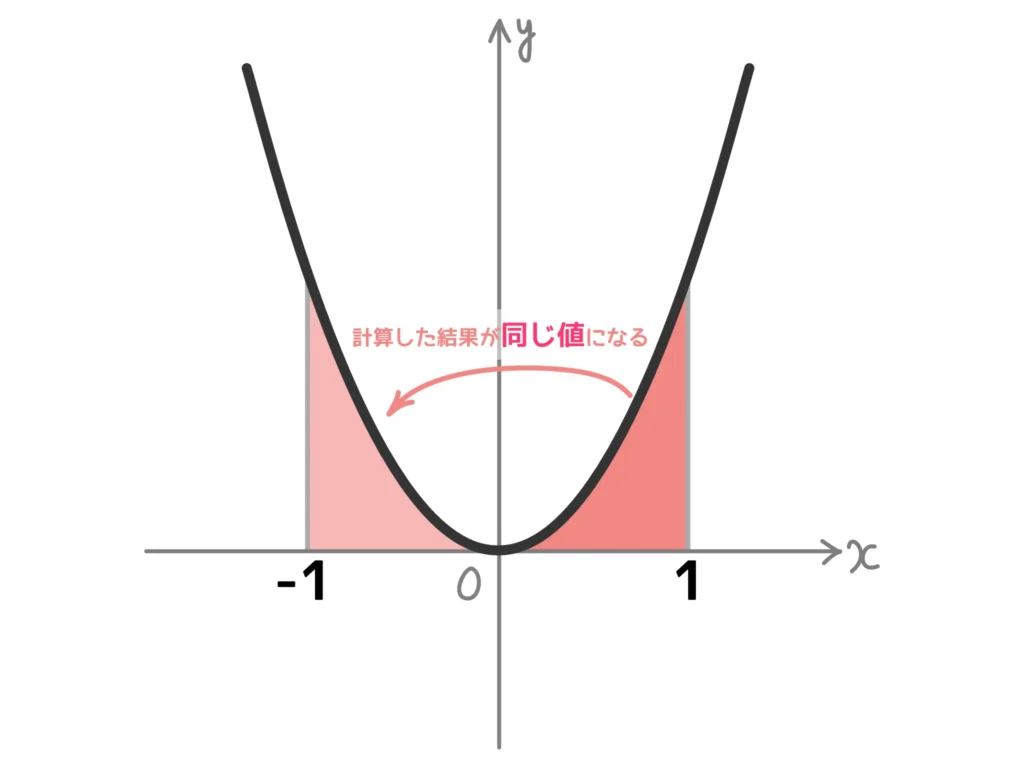
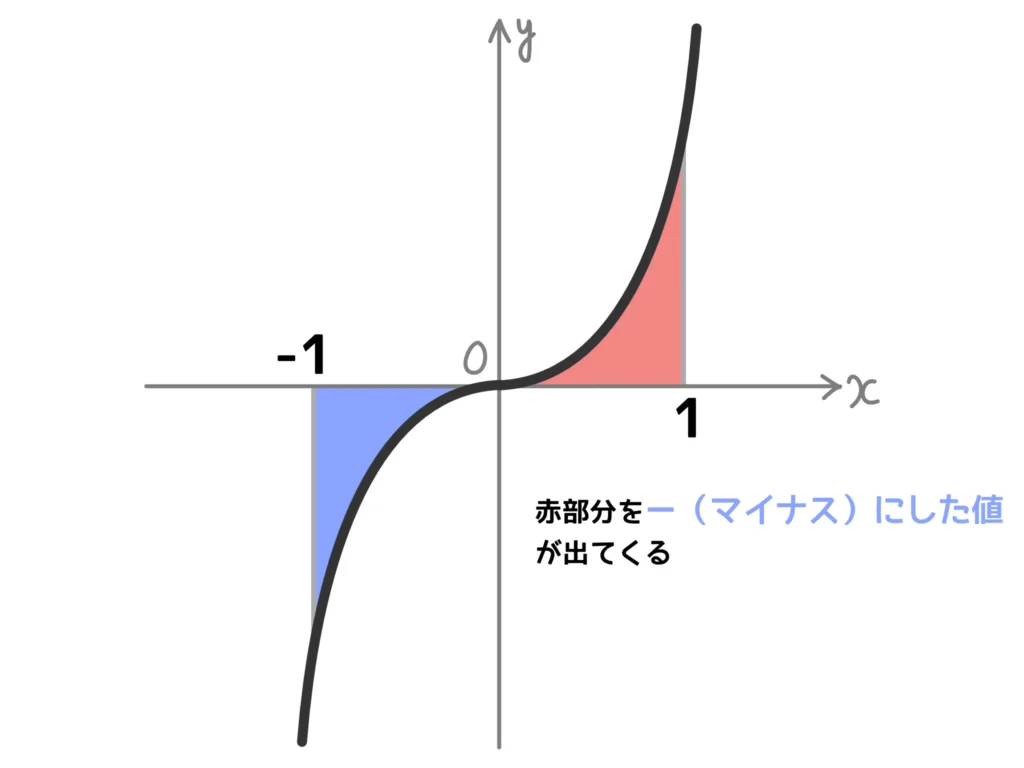
\(\displaystyle \int_{-1}^1 x^2 dx = 2 \int_{0}^1 x^2 dx \)
\(\displaystyle \quad = 2 \left[ \frac{1}{3}x^3 \right]_{0}^{1} = \frac{2}{3} \)

\(\displaystyle \int_{-1}^1 x^3 dx = 0\)

また、数学Ⅲの問題で出てくるような関数には対称性を持つものがかなりあります。

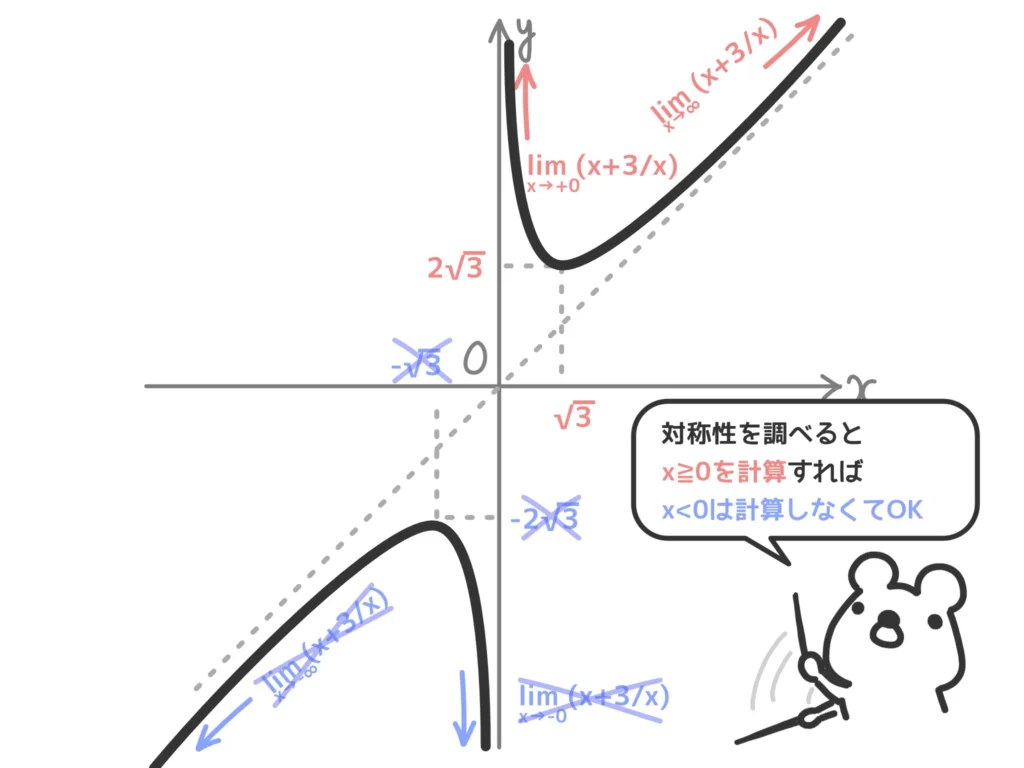
例．\(\displaystyle f(x) = x + \frac{3}{x} \)

\(x \to -x\)とすると、\(\displaystyle f(-x) = -x + \frac{3}{-x} = – \left( x + \frac{3}{x} \right) = -f(x) \)なので、原点対称。

対称性が確認できれば、\(x \geq 0\)（今回は\(x > 0\)ですが）のグラフ、というか増減表をかけばOKです。

なぜなら\(x < 0\)の部分はそれをひっくり返せばいいからです。

数学Ⅲのグラフは、極値を求めたり極限を求めたり、とにかく計算が大変です。対称性がわかれば計算量は４割引です。

せんせ

20分かかる問題が12分で解けると思えばかなりの時短ですよね。特に、テストのように限られた時間内に解かないといけない状況では、こうかはばつぐんです。

偶関数・奇関数と積分

偶関数・奇関数を調べることのメリットは積分だけではありませんが、積分計算では重要な性質として押さえられることが多いので、一応まとめておきます

偶関数・奇関数と積分

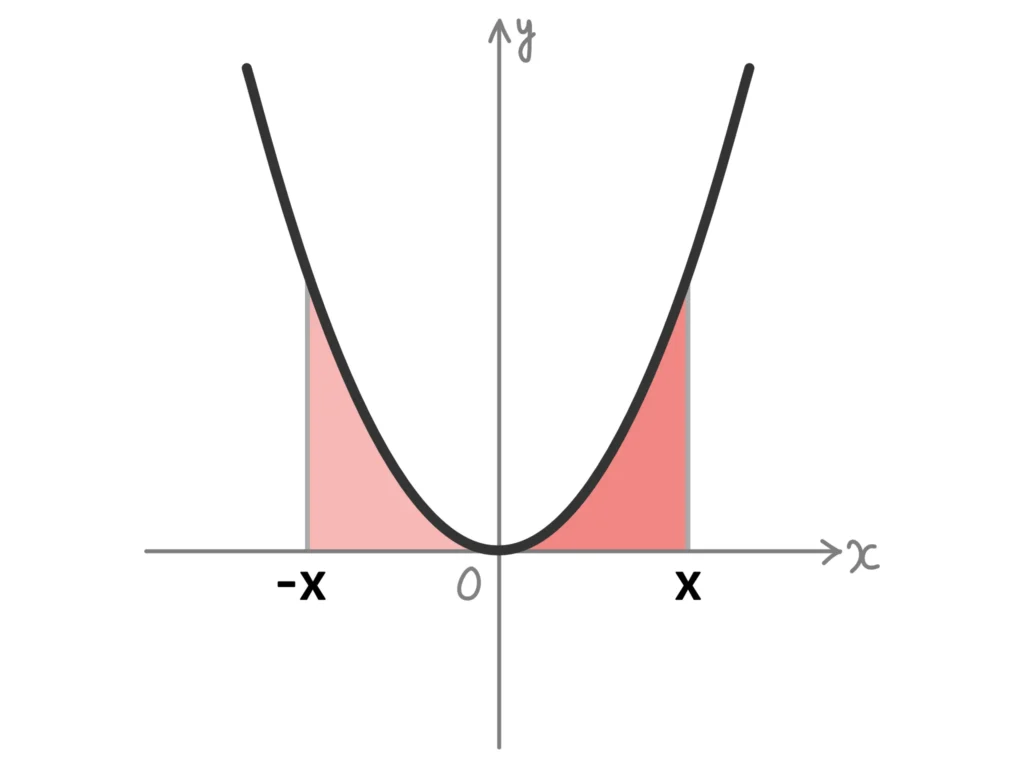
前提として、積分区間が\(-a \leq x \leq a\)のように、\(0\)をはさんで対称でないと使えません。

\(f(x)\)が偶関数であるとき、

\(\displaystyle \int_{-a}^{a}f(x)dx = 2\int_{0}^{a}f(x)dx\)

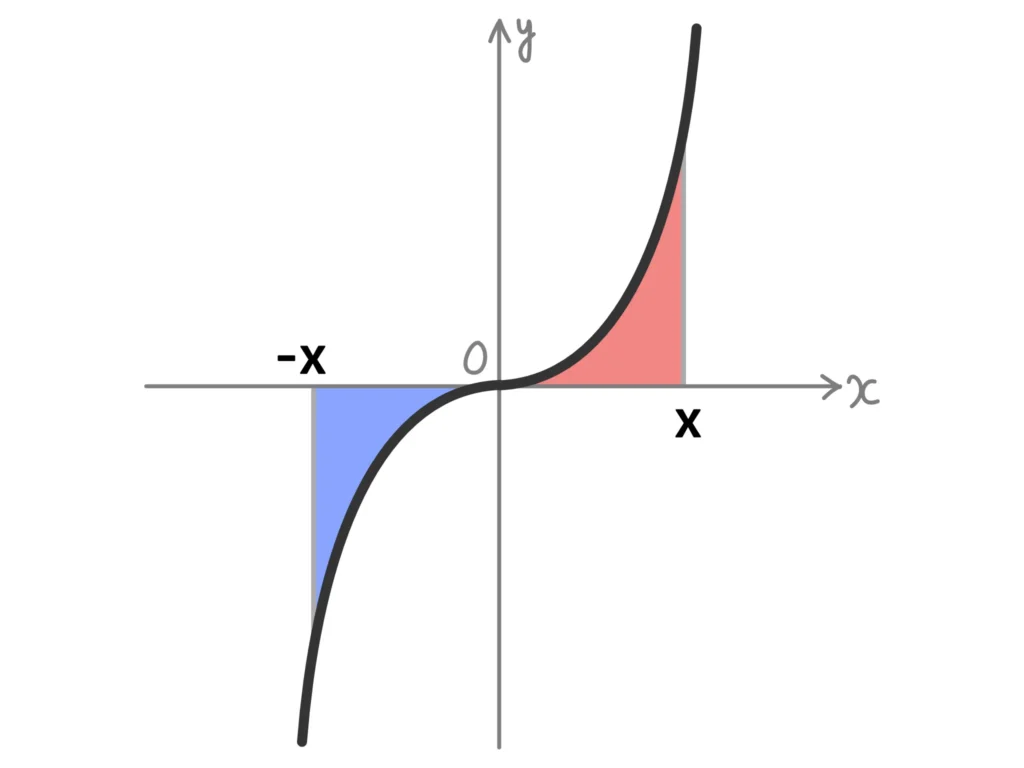
\(g(x)\)が奇関数であるとき、

\(\displaystyle \int_{-a}^{a}g(x)dx = 0\)

証明はコチラ（数学Ⅲの置換積分を使います）

「置換積分って？」という人はコチラの記事もごらんください。

（証明）

\(f(x)\)を偶関数とする。つまり、\(f(-x) = f(x)\)が成り立つ。

\(\displaystyle \int_{-a}^{a}f(x)dx = \int_{-a}^{0}f(x)dx + \int_{0}^{a}f(x)dx\)

ここで、\(\displaystyle \int_{-a}^{0}f(x)dx\)の\(x = -t\)と置換すると、

\(dx = -dt\)、\(x: -a \to 0\)のとき\(t: a \to 0\)なので、

\(\displaystyle \int_{-a}^{0}f(x)dx = \int_{a}^{0}f(-t)(-dt)=\int_{0}^{a}f(t)dt\)（\(f(-t) = f(t)\)なので）

よって、\(\displaystyle \int_{-a}^{0}f(x)dx = \int_{0}^{a}f(t)dt = \int_{0}^{a}f(x)dx\)（見た目の文字の問題だけなので、\(t\)を\(x\)に変えてもOK）

したがって、
\(\displaystyle \int_{-a}^{a}f(x)dx = \int_{-a}^{0}f(x)dx + \int_{0}^{a}f(x)dx\)
\(\displaystyle \quad = \int_{0}^{a}f(x)dx + \int_{0}^{a}f(x)dx = 2\int_{0}^{a}f(x)dx\)（終）

また、\(g(x)\)を奇関数とする。つまり、\(g(-x) = -g(x)\)が成り立つ。

\(\displaystyle \int_{-a}^{a}g(x)dx = \int_{-a}^{0}g(x)dx + \int_{0}^{a}g(x)dx\)

ここで、\(\displaystyle \int_{-a}^{0}g(x)dx\)の\(x = -t\)と置換すると、

\(dx = -dt\)、\(x: -a \to 0\)のとき\(t: a \to 0\)なので、

\(\displaystyle \int_{-a}^{0}g(x)dx = \int_{a}^{0}g(-t)(-dt)=-\int_{0}^{a}g(t)dt\)

よって、\(\displaystyle \int_{-a}^{a}g(x)dx = \int_{-a}^{0}g(x)dx + \int_{0}^{a}g(x)dx = – \int_{0}^{a}g(x)dx+ \int_{0}^{a}g(x)dx=0\)（終）

グラフの対称性の調べ方のコツ

それでは具体的にどうやって対称性があるか？を調べる方法について説明します。

先ほどたろうくんが、

たろぅ

んー…まぁ「対称な」ってとこはわかりますけど、「\(f(-x) = f(x)\)」とか「\(f(-x) = -f(x)\)」ってのがよく意味がわかんないんですけど…。

と言っていましたが、この式の意味がわかれば大丈夫です。

イメージとしては、

とにかく\(f(x)\)の\(x \to -x\)としてみる（\(f(-x)\)の形を作る）。
もし、これが元の関数と形が変わらなければ（\(f(-x) = f(x)\)）なら、\(y\)軸対称。元の関数全体にー（マイナス）をつけた形（\(f(-x) = -f(x)\)）なら原点対称。

という感じです。グラフ的な話でいうと、次のようなイメージですね。

せんせ

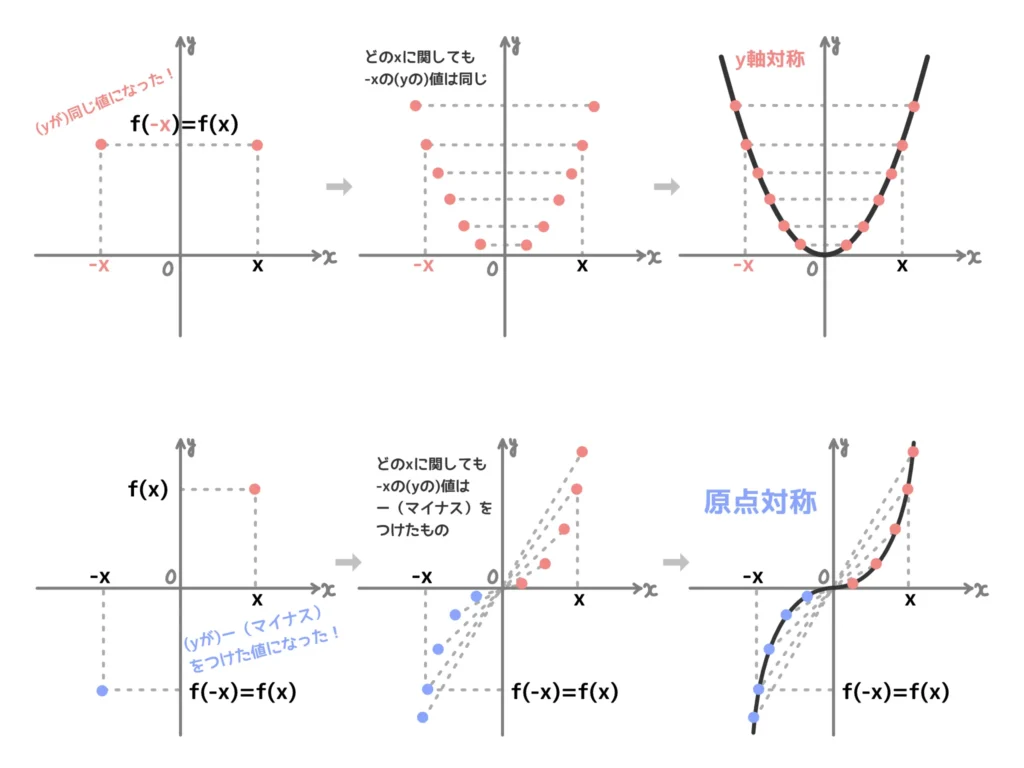
とりあえず\(x \to -x\)としてみる、つまり、\(y\)軸をはさんで反対側の値はどうなっているか？というとこからスタートです。
もし値が変わらなければ\(y\)軸対称、ー（マイナス）をつけた形になれば原点対称です。

ちなみに、次のような関数の感覚をもっていると、\(x \to -x\)にしたときに、「形が変わらない」か「ー（マイナス）をつけた形になる」か判断しやすいです。（実際には与えられた関数の形によるので、あくまで参考程度でお願いします。）

形が変わらない関数

偶数乗の整関数、分数関数：\(x^2\)、\(x^4\)、\(\displaystyle \frac{1}{x^2}\)、…
\(\cos{x}\)
絶対値：\( |x| \)（\( |x + 1|\)とかはダメなので、形によります）
定数

ー（マイナス）をつけた形になる関数

奇数乗の整関数、分数関数：\(x\)、\(x^3\)、\(\displaystyle \frac{2}{x}\)…
\(\sin{x}\)、\(\tan{x}\)

他には、関数全体として対称性をもっていると、偶関数や奇関数になるときがあります。

例．\( y = e^x\)は\(y\)軸対称でも原点対称でもありませんが、\(\displaystyle y = \frac{e^x + e^{-x}}{2}\)は\(y\)軸対称（偶関数）です。

（\(x \to -x\)とすると、\(\displaystyle y = \frac{e^{-x} + e^{x}}{2}=\frac{e^x + e^{-x}}{2}\)）

ちなみに、ここまでの話でわかったと思いますが、偶関数・奇関数の「偶・奇」は整関数の偶数乗・奇数乗のことです。（偶関数：\(x^2\)、\(x^4\)、…、奇関数：\(x\)、\(x^3\)、）

また、\(x \to -x\)として対称性を調べるときに、

偶関数→そのままの形、奇関数→ー（マイナス）をつけた形

なので、整数の偶数・奇数のイメージというよりは、

偶関数→＋（プラス）、奇関数→ー（マイナス）

のイメージをもっておいた方がいいです。

せんせ

偶関数→＋（プラス）、奇関数→ー（マイナス）
の感覚をもっておくと、次の偶関数や奇関数の足し算や掛け算のイメージがしやすいです。

偶関数・奇関数の和や積

偶関数や奇関数の足し算や掛け算については次のような性質があります。

偶関数＋偶関数＝偶関数（⊕＋⊕＝⊕）
奇関数＋奇関数＝奇関数（⊖＋⊖＝⊖）
偶関数×偶関数＝偶関数（⊕×⊕＝⊕）
奇関数×奇関数＝偶関数（⊖×⊖＝⊕）
偶関数×奇関数＝奇関数（⊕×⊖＝⊖）

例．

\(x^2 + \cos{x}\)は偶関数
\(x + \sin{x}\)は奇関数
\(x^2 \cos{x}\)は偶関数
\(x \sin{x}\)は偶関数
\(x^2\sin{x}\)は奇関数

ホントに？という疑い深い人はコチラ

例えば、\(f(x)\)を偶関数（\(f(-x) =f(x)\)）、\(g(x)\)も偶関数（\(g(-x) =g(x)\)）とすれば、

関数\(f(x) + g(x)\)を考えて\(x \to -x\)としたときに、\(f(-x) + g(-x) = f(x) + g(x)\)（変わらない）となることや、

関数\(f(x) g(x)\)を考えて\(x \to -x\)としたときに、\(f(-x) g(-x) = f(x) g(x)\)（変わらない）となることがわかりますし、

\(f(x)\)を奇関数（\(f(-x) =-f(x)\)）、\(g(x)\)も奇関数（\(g(-x) =-g(x)\)）とすれば、

関数\(f(x) + g(x)\)を考えて\(x \to -x\)としたときに、\(f(-x) + g(-x) = -f(x) – g(x)=-(f(x) + g(x))\)（ー（マイナス）をつけた形）となることや、

関数\(f(x) g(x)\)を考えて\(x \to -x\)としたときに、\(f(-x) g(-x) = -f(x)(- g(x))=f(x)g(x)\)（変わらない）となることがわかります。

また、\(f(x)\)を偶関数（\(f(-x) =f(x)\)）、\(g(x)\)を奇関数（\(g(-x) =-g(x)\)）とすれば、

関数\(f(x) g(x)\)を考えて\(x \to -x\)としたときに、\(f(-x) g(-x) = f(x)(- g(x))=-f(x)g(x)\)（ー（マイナス）をつけた形）となることがわかります。

せんせ

やはり、偶関数→＋（プラス）、奇関数→ー（マイナス）というイメージの方がわかりやすいですね。

偶関数・奇関数とグラフの対称性まとめ

偶関数・奇関数とグラフの対称性のお話でした。

偶関数・奇関数は積分計算の簡略化の話をすることが多いですが、実際には対称性を意識することはかなり重要です。

グラフをかくときにも計算量削減になりますし、因数分解などでも対称性が崩れている文字に着目したりします。

ぜひ対称性を意識してみて下さい！

せんせ

対称性、大事。