PR
漸化式の応用問題【ここまで押さえておけば安心!】

漸化式はまず、基本パターンの解き方を押さえておくべきですが、それだけでは漸化式の応用問題を解くのが難しいです。
 せんせ
せんせちなみに、「漸化式の基本パターンもちょっと不安…」という人はコチラの記事もご覧ください。




この記事では、漸化式の応用問題でよく出てくるパターンと解き方のコツについて説明していきます。
漸化式の応用問題
(調理実習中…)



…この冷やし中華のキュウリの千切り作ったの…たろうくんね?



え…そうだけど?なんかマズイことしたかな?普通に千切りにしただけだけど…。



切り方が違うわ!最初はナナメに薄切りするの!で、それを千切りにするのよ!そうしないと皮部分が偏るでしょ!



えー…細かい…。



キュウリの千切りは最初の変形が重要なのよ!



(ん?変形?)
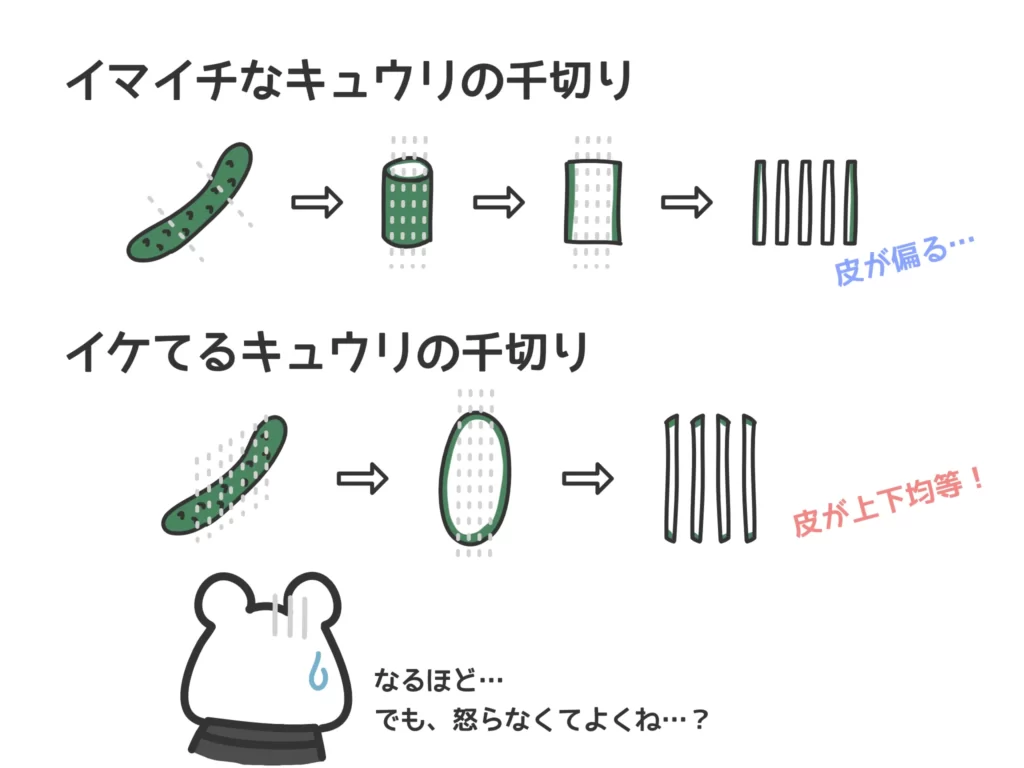

ということで(←?)、漸化式の応用問題です。
まず、漸化式の応用問題全般の注意点としては、
- 最初の変形の一手が最大のポイントになることが多い。というかほとんど。
- 誘導が用意されていることも多い。
ですね。特に「最初の変形の一手が最大のポイント」というところですね。



実はそこを超えれば、あとはほとんど解き方は同じような感じになっていきます。
同じような感じ…というのは、具体的に言うと、
最初の変形で出てきた漸化式を置き換えることで、漸化式基本パターンのいずれかの形になることが多い、
です。



特に、基本パターンの\( a_{n+1} = pa_n + q\)になることが多いです。サッと解けるように練習しておきましょう。
漸化式の応用\(a_{n+1} = p a_n+\)(\(n\)の式)
\(a_{n+1} = p a_n+\)(\(n\)の式)は\(p\)が無ければ基本形の「階差数列」で解けます。
ですが、この\(p\)があるだけで途端に解けなくなるんですよね…。



それでは具体的な問題を見ていきましょう。
\(a_{n+1} = p a_n+\)(\(n\)の一次式)
例.\(a_{n+1} = 2 a_n + n + 1\)、\(a_1 = 1\)
まずはこの形ですね。右辺に\(n\)の二次式がくっついてるケース…もあり得ますが、ハードルはかなり高くなります。
基本は「1つ進めた式を作って、引く」という方法で解いていきます。



この「1つ進めた式を作る」というのはよくやるので、押さえておいてほしいですね。感覚としては\(n \rightarrow n+1\)に置き換える、という感じです。
(解答)
\(a_{n+1} = 2 a_n + n + 1\)…① より、
\(a_{n+2} = 2 a_{n+1} + (n+1) + 1\)(←ここがポイント)
\(a_{n+2} = 2 a_{n+1} + n + 2\)…②
②ー①
\(a_{n+2} – a_{n+1} = 2 a_{n+1} – 2 a_n + 1\)
\(a_{n+2} – a_{n+1} = 2 (a_{n+1} – a_n) + 1\)
\( a_{n+1} – a_n = b_n\)と置くと、(\( b_{n+1} = a_{n+2} – a_{n+1}\)なので)
\(b_{n+1} = 2b_n + 1\)
\(b_{n+1} + 1 = 2(b_n + 1)\)
数列{\(b_n + 1\)}は、
初項\(b_1+1 = a_2 -a_1 + 1 = (2a_1 + 1 +1) – a_1+1 \)
\( =a_1 +3 = 4\)、公比2の等比数列なので、
\( b_n + 1 = 4 \cdot 2^{n-1}\)
\( b_n = 4 \cdot 2^{n-1} -1\)
\( a_{n+1} – a_n = 4 \cdot 2^{n-1} -1\)
よって、{\(a_n\)}の階差数列の一般項が\(4 \cdot 2^{n-1} -1\)となるので、
\( n \geq 2\)のとき
\(\displaystyle a_n = a_1 + \sum_{k=1}^{n-1}(4 \cdot 2^{k-1} -1)\)
\(\displaystyle \quad = 1 + \frac{4(2^{n-1}-1)}{2-1} -(n-1)\)
\(\displaystyle a_n = 2^{n+1}-n-2\)
これは\(n=1\)のときも成り立つ。
よって\(\displaystyle a_n = 2^{n+1}-n-2\)…(答)



ちなみに、よくやる別解も載せておきます。
こっちの方が計算はラクですし、漸化式を解くときの本質が見えます。
\(n\)の1次式を上手くバラす方法
コチラの記事で説明したように、漸化式は「自分の都合のいい形に変えたモン勝ち」のような側面があります。
特に今回は、上記の解法だと「1つ進めた式を作って、引く」→「特性方程式使って解く」→「階差数列を使って解く」という流れになり、面倒な上にミスをしやすいです。



特に階差数列って、シグマもあるし、解答のかき方も面倒なのであんまりやりたくないんですよね…。
ということで、上手く\(n\)の1次式をバラします!
(別解)
\(a_{n+1} = 2 a_n + n + 1\)が
\(a_{n+1} + p(n+1)+q = 2( a_n + pn +q)\)の形になるように変形する。(←ここがポイント)
\(a_{n+1} + p(n+1)+q = 2( a_n + pn +q)\)を展開してまとめると、
\(a_{n+1} = 2 a_n + pn -p +q\)
これが\(a_{n+1} = 2 a_n + n + 1\)と一致していればいいので、
\(p = 1\)かつ\(-p+q = 1\)。よって、\(p=1\)、\(q =2\)
したがって、与えられた漸化式は、
\( a_{n+1} + (n+1) + 2 = 2(a_n + n+2 )\)と変形できる。
\(a_n + n+2 = b_n\)と置くと、
\(b_{n+1} = 2b_n\)
数列{\(b_n\)}は、初項\( b_1 = a_1 + 1 + 2 = 4\)、公比2の等比数列。
\(b_n = 4 \cdot 2^{n-1}\)
\(a_n + n + 2 = 2^{n+1}\)
\(a_n = 2^{n+1} -n -2\)…(答)
【補足】
見て分かる通り、\(p\)、\(q\)の値が定まった後はメチャクチャ簡単です。
発想としては、与えられた漸化式を
\(a_{n+1} + \)(右辺の①を\(n+1\)にしたもの) \(= 2( a_n\)+(\(n\)の1次式①)\()\)
の形にしたい!というところから始まります。(右辺の最初の2は与えられた漸化式の\(a_n\)の係数に揃えています。)
そうすることで、右辺の\(a_n\)+(\(n\)の1次式①)\(=b_n\)と置けば、
(左辺) \(=b_{n+1}\)なので、
\(b_{n+1} = 2b_n\)となって等比数列を使って解ける、という流れです。
変形のイメージは、与えられた漸化式の\(n+1\)の部分を上手く左辺と右辺に振り分ける感じですね。
このときのポイントは、\(a_{n+1} + p(n+1)+q = 2( a_n + pn +q)\)の左辺の形ですね。
右辺の\(a_n + pn +q\)を \( b_n\)と置きたいので、左辺は\(b_{n+1}\)、つまり、
\(b_{n+1} = a_{n+1} +p(n+1)+q\)としなければならない、ということになります。



\(a_n + pn +q\)の\(n \rightarrow n+1\)とするなら、\(pn\)の\(n\)も\(n+1\)にしないといけない、ということですね。逆に言うと、その形をキープしていれば左辺は\(b_{n+1}\)に置き換えることができます!
\(a_{n+1} = p a_n+\)(\(r^n\)の式)
このパターンは三項間漸化式など、応用できるケースが結構多いので、できれば最初の一手を覚えておいたほうがいい形ですね。



とはいえ、最初の一手はそこまで難しくないので覚えておいて下さい。逆に誘導がない場合は覚えていないと、この発想は出てこないと思います。
例.\(a_{n+1} = 4 a_n + 2^{n+1}\)、\(a_1 = 2\)
ここの見出しで便宜上\(r^n\)と書いていますが、\(n\)乗である必要はありません。今回のように\(n+1\)乗でも\(n-1\)乗でも同じです。
結論から言うと、全体を\(r^{n+1}\)で割ってやります。



必ず\(r^{n+1}\)です!与えられた漸化式の最後の部分が\(n\)乗でも\(n-1\)乗でも、必ず\(r^{n+1}\)で割ります!
今回は\(a_{n+1} = 4 a_n + 2^{n+1}\)なので、\(2^{n+1}\)で割ってやります。
(解答)
\(a_{n+1} = 4 a_n + 2^{n+1}\)の、両辺を\(2^{n+1}\)で割ると(←ここがポイント)
\(\displaystyle \frac{a_{n+1}}{2^{n+1}} = \frac{4 a_n}{2^{n+1}} + 1\)
\(\displaystyle \frac{a_{n+1}}{2^{n+1}} = \frac{4 a_n}{2 \cdot 2^{n}} + 1\)
\(\displaystyle \frac{a_{n+1}}{2^{n+1}} = 2 \frac{a_n}{2^{n}} + 1\)
\(\displaystyle \frac{a_n}{2^{n}} = b_n\)とおくと、(\(\displaystyle b_{n+1}\ = \frac{a_{n+1}}{2^{n+1}}\)なので)
\(b_{n+1} = 2b_n + 1\)
\(b_{n+1}+1 = 2(b_n + 1)\)
数列{\(b_n + 1\)}は初項\(\displaystyle b_1 + 1 = \frac{a_1}{2^{1}}+1 = 1 + 1 = 2 \)、公比2の等比数列。
\(b_n + 1 = 2 \cdot 2^{n-1}\)
\(b_n = 2^n -1\)
\(\displaystyle \frac{a_n}{2^{n}} = 2^n -1\)
\(a_n = 2^n(2^n-1)\)…(答)
【補足】
\(r^{n+1}\)で割るのは左辺を\(\displaystyle b_{n+1}\ = \frac{a_{n+1}}{r^{n+1}}\)としたいからです。
右辺の\(r^{n+1}\)の\(a_n\)にかかる部分は、
\(\displaystyle \frac{p a_n}{r^{n+1}} = \frac{p a_n}{r \cdot r^{n}} = \frac{p}{r}\cdot \frac{a_n}{r_n}\)とすることで、調整が可能なんですね。



なので、必ず\(r^{n+1}\)で割ります!右辺は指数法則で調整してください!
漸化式の応用「逆数をとる」
例.\(\displaystyle a_{n+1} = \frac{a_n}{2a_n + 3}\)、\(\displaystyle a_1 = \frac{1}{2}\)
結論から言うと、こういう分数がからんでいるときは逆数をとると効果的です。



100%、とはいいませんけどね。逆数にしたときに\(\displaystyle \frac{1}{a_n} = b_n\)と置き換えられそうなときには有効です。
解答の注意点としては、逆数をとるときに分母に\(a_n\)がくる可能性があります。
ということは、どんな自然数\(n\)に対しても\(a_n \neq 0\)であることを示しておかないといけません。



ただ、解答の本筋ではないので、軽く説明程度で大丈夫です。
(解答)
\(\displaystyle a_1 = \frac{1}{2}\)と\(\displaystyle a_{n+1} = \frac{a_n}{2a_n + 3}\)より、\(a_2 \neq 0\)、\(a_3 \neq 0\)…となり、すべての自然数\(n\)について、\(a_n \neq 0\)。
\(\displaystyle a_{n+1} = \frac{a_n}{2a_n + 3}\)の両辺逆数をとって、
\(\displaystyle \frac{1}{a_{n+1}} = \frac{2a_n + 3}{a_n} = 3 \cdot \frac{1}{a_n} + 2 \)
ここで、\(\displaystyle \frac{1}{a_n} = b_n\)とおくと(\(\displaystyle \frac{1}{a_{n+1}} = b_{n+1}\)なので)
\( b_{n+1} = 3b_n + 2 \)
\( b_{n+1} + 1 = 3(b_n + 1)\)
数列{\(b_n + 1\)}は初項\(\displaystyle b_1 + 1 = \frac{1}{a_1} + 1 = 2 + 1 = 3\)、公比3の等比数列なので、
\(b_n + 1 = 3 \cdot 3^{n-1}\)
\(b_n = 3^n – 1\)
\(\displaystyle \frac{1}{a_n} = 3^n – 1\)
\(\displaystyle a_n = \frac{1}{3^n – 1}\) … (答)
【補足】
最初の\(a_n \neq 0 \)の証明、というか説明は次のようにしてもOKです。
(別の説明方法)
\(a_n = 0\)となる\(n\)があるとすると、\(\displaystyle a_{n+1} = \frac{a_n}{2a_n + 3}\)より、\(a_{n-1} = 0\)。これを繰り返すと\( a_1 = 0\)となり矛盾するので、すべての自然数\(n\)で\( a_n \neq 0 \)。
この方法は実は背理法です。「すべての自然数\(n\)で\( a_n \neq 0 \)」という結論を否定すると「\(a_n = 0\)となる\(n\)が存在する」となります。この否定した結論から矛盾を導いています。
ちなみに、先程の説明の方法、
\(\displaystyle a_1 = \frac{1}{2}\)と\(\displaystyle a_{n+1} = \frac{a_n}{2a_n + 3}\)より、\(a_2 \neq 0\)、\(a_3 \neq 0\)…となり、すべての自然数\(n\)について、\(a_n \neq 0\)。
は数学的帰納法のイメージですね。
\( a_1 \neq 0\)で、\(\displaystyle a_{n+1} = \frac{a_n}{2a_n + 3}\)という形から、\(a_2 \neq 0\)だし、その次の\(a_3 \neq 0 \)だし、…全部の項は帰納法的に0じゃないよね、という説明をしている感じです。
漸化式の応用「対数をとる」
例.\(a_{n+1} = 2^n a_n\)、\(a_1 = 2\)
複雑な積の形であれば、対数をとることもあります。



対数の形にすれば、積ベースの式を和ベースに直すことができるので処理がしやすくなります。
逆数をとるときと一緒ですが、真数条件の確認だけはしておきましょう。
(解答)
\(a_{n+1} = 2^n a_n\)、\(a_1 = 2\)より、すべての\(n\)について\(a_n > 0\)。
よって、\(a_{n+1} = 2^n a_n\)の両辺は正なので、底2の対数をとると、
\( \log_2{a_{n+1}} = \log_2{ ( 2^n a_n )}\)
\( \log_2{a_{n+1}} = \log_2{ 2^n } + \log_2{ a_n }\)
\( \log_2{a_{n+1}} = \log_2{ a_n } + n \)
\( \log_2{a_n} = b_n\)とおくと、
\(b_{n+1} = b_n + n\)
数列{\(b_n\)}の階差数列の一般項は\(n\)なので、
\(n \geq 2\)のとき
\(\displaystyle b_n = b_1 + \sum_{k=1}^{n-1} k\)
\(\displaystyle \quad = \log_2{a_1} + \frac{1}{2}n(n-1)\)
\(\displaystyle \quad = \log_2 2 + \frac{1}{2}n(n-1)\)
\(\displaystyle b_n = \frac{1}{2}(n^2-n+2)\)
これは\(n=1\)のときも成り立つ。よって、
\(\displaystyle b_n = \frac{1}{2}(n^2-n+2) \cdot 1\)
\(\displaystyle \log_2{a_n} = \frac{1}{2}(n^2-n+2)\log_2 2\)
\(\displaystyle \log_2{a_n} = \log_2 {2^{\frac{1}{2}(n^2-n+2)}}\)
\(\displaystyle a_n = 2^{\frac{1}{2}(n^2-n+2)} = \sqrt{2}^{n^2-n+2}\)…(答)
【補足】
ちなみに、底は底の条件を満たせば、どんな値でも問題ありません。
例えば今回の問題で「底3の対数」をとっても、最後の答えの形は変わりますが、解くことができます。



ちなみに「底3の対数」をとったときの答えは\(a_n = \sqrt{3}^{\log_{3}2(n^2-n+2)}\)となります。



え…?じゃあ底の選び方によって無数に解答があるってこと?
まぁ…半分正解、半分間違い、という感じでしょうか。実は指数関数にも「底の変換」があります。これによって底の形が変わっているだけなんですね。詳しくはこちらの記事をご覧ください。


漸化式の応用「上手いこと変形する」
例.\( n a_{n+1} = (n+1)a_n + 1\)、\(a_1 = 1\)
\( n a_{n+1} \)と\( (n+1)a_n\)の\(n\)と\(n+1\)が互い違いに掛け合わさっています。こういうときは\(n(n+1)\)で割ると上手く置き換えることができます。
(解答)
\( n a_{n+1} = (n+1)a_n + 1\)の両辺を\(n(n+1)\)で割ります。
\(\displaystyle \frac{a_{n+1}}{n+1} = \frac{a_n}{n} + \frac{1}{n(n+1)}\)
\(\displaystyle \frac{a_n}{n} = b_n\)とおくと、
\(\displaystyle b_{n+1} = b_n + \frac{1}{n(n+1)}\)
数列{\(b_n\)}の階差数列の一般項は\(\displaystyle \frac{1}{n(n+1)}\)なので、
\(n \geq 2\)のとき
\(\displaystyle b_n = b_1 + \sum_{k=1}^{n-1} \frac{1}{k(k+1)}\)
\(\displaystyle \quad = \frac{a_1}{1} + \sum_{k=1}^{n-1} \left( \frac{1}{k}-\frac{1}{k+1} \right) \)
\(\displaystyle \quad = 1 + \left( \frac{1}{1}-\frac{1}{2} \right)+ \left( \frac{1}{2}-\frac{1}{3} \right)+\cdots+ \left( \frac{1}{n-1}-\frac{1}{n} \right) \)
\(\displaystyle \quad = 1 + 1 -\frac{1}{n}\)
\(\displaystyle b_n = \frac{2n-1}{n}\)
これは\(n=1\)のときも成り立つ。よって、
\(\displaystyle b_n = \frac{2n-1}{n}\)
\(\displaystyle \frac{a_n}{n} = \frac{2n-1}{n}\)
\(a_n = 2n-1\)…(答)
漸化式の応用の練習問題
問.条件、\(a_{n+1} = 3 a_n + n^2 + 2n\)、\(a_1 = 1\)…①について、次の各問いに答えよ。
(1) \(a_{n+1}+p(n+1)^2+q(n+1)+r = 3 ( a_n + pn^2 + qn + r ) \)となる\(p\)、\(q\)、\(r\)の値を求めよ。
(2) 条件①によって定められる数列{\(a_n\)}の一般項を求めよ。
答え
(1) \(\displaystyle p = \frac{1}{2}\)、\(\displaystyle q = \frac{3}{2}\)、\(r=1\)
(2) \(\displaystyle a_n = 4 \cdot 3^{n-1} -\frac{1}{2}n^2 – \frac{3}{2}n-1\)
問.条件、\(a_{n+1} = 2^n \cdot 3^n \cdot a_n\)、\(a_1 = 10\)について、次の各問いに答えよ。
(1) 条件によって定められる数列{\(a_n\)}の一般項\(a_n\)を、\(a_n = 10^{□}\)の形で求めよ。
(2) 数列{\(a_n\)}の項\(a_k\)が、初めて10桁以上になるときの\(k\)の値を求めよ。ただし、常用対数表を使ってよい。
答え
(1) \(\displaystyle a_n = 10^{\displaystyle \frac{\log_{10}2 + \log_{10}3}{2} n(n-1)+1 } \)
(2) \(k=6\)
漸化式の応用まとめ
よくある漸化式の応用問題のまとめでした。
誘導があることがほとんどなので、基本的に解法を覚えておく必要はありません。
ですが、誘導も「\(\displaystyle \frac{1}{a_n} = b_n\)と置くことにより…」程度であることも多いので、それぞれの解き方を一度は経験しておく必要があるかなと思います。



記事の中で説明していますが、個人的には「\(r^{n+1}\)で割る」方法は覚えておいてもいいかな、と思います。\(r^{n}\)で割るミスをするとわかりにくくなりますし、三項間漸化式でも使ったり、意外と応用範囲が広いからです。






