PR
置換積分の計算方法のコツとその本質【いくつかのパターン別に解説】

高校の数学IIIで習う積分。高校数学の花形ですね。
その積分の計算方法として、置換積分というものがあります。
この置換積分…計算上よく間違える積分方法ですので、ポイントを押さえながら解説をしていきます。
 せんせ
せんせ最後にちょっとした個人的な意見も載せておきます。
置換積分とは?
置換積分とは、積分において、変数を置き換えて計算する方法のことです。



わざわざ言葉で説明するようなことじゃなかったですね…笑。
もちろん、不定積分でも置換積分はできます!
置換積分
\( y = f(x) \)について、\(\displaystyle \int_a^b f(x)dx \)を考えます。
\(x = g(t)\)と置き換えて、\(\alpha\)、\(\beta\)を、\(a = g(\alpha)\)、\(b = g(\beta)\)(要は\(\alpha\)、\(\beta\)は\(x=a,b\)に対応する\(t\)の値)とすると、
\(\displaystyle \int_a^b f(x)dx = \int_{\alpha}^{\beta}f(g(t))g'(t)dt \)
と計算することができます。
(説明)
まず、\( y = f(x) \)について、\(\displaystyle \int f(x)dx \)を考えます。
\(\displaystyle \int f(x)dx = F(x) + C \)とすると、これらを両辺\(t\)で微分します。
\(\displaystyle \frac{d}{dt} \int f(x)dx = \frac{d}{dt} \{ F(x) + C \} \)
\(\displaystyle \frac{d}{dx} \int f(x)dx \cdot \frac{dx}{dt} = \frac{d}{dt} F(x) \)(左辺は合成関数の微分。右辺の積分定数\(C\)は微分したら消える。)
\(x=g(t)\)より、\(\displaystyle \frac{d}{dx} \int f(x)dx=f(x)=f(g(t)) \)、\(\displaystyle \frac{dx}{dt}=g'(t)\)なので、
\(\displaystyle f(g(t)) g'(t) = \frac{d}{dt} F(x) \)
両辺\(t\)で積分して、
\(\displaystyle \int f(g(t))g'(t)dt = F(x) = \int f(x)dx \)
\(x: a \rightarrow b\)のとき、\(t: \alpha \rightarrow \beta \)なので、積分区間まで考えると、
\(\displaystyle \int_a^b f(x)dx = \int_{\alpha}^{\beta}f(g(t))g'(t)dt \)



ぶっちゃけわかりにくいので、実際にポイントを押さえながら計算していきましょう!
置換積分の例
置換積分は\(x\)に関する部分を全て\(t\)に置き換える、のがコツです。
具体的には
- 関数部分
- 積分区間
- \(dx\)
です。特に積分区間と\(dx\)を\(t\)に置き換え忘れることが多いので、その点は注意しながら置き換えていってください。
積分区間の変換はわかりやすいのですが、問題は\(dx\)の変換ですね。ここで、
\(\displaystyle \int_a^b f(x)dx = \int_{\alpha}^{\beta}f(g(t))g'(t)dt \)
を見ると、\(dx\)の部分を\(g'(t)dt\)に置き換えています。
つまり、\(x=g(t)\)としたときに\(t\)で微分した\(g'(t)\)と\(dt\)をくっつけて、\(dx\)と置き換えればいい、ということになります。



ただ、いつも\(x=g(t)\)とキレイに置き換えられるとは限りません。そういうときにどうすればいいか…は次の例題を解きながら説明していきます!
それでは、例をいくつかあげるので実際に計算してみましょう。
例1.\(\displaystyle \int (2x+1)^5 \cdot 4x dx \)
例1の解答
(解答)
\((2x+1)^5\)は展開するのが面倒なので、この\(2x+1=t\)と置き換えます。
\(\displaystyle x = \frac{1}{2}t – \frac{1}{2} \) として、\(\displaystyle dx = \frac{1}{2}dt\)と計算してもいいですが、
\(2x+1=t\)を、形式的に左辺を\(x\)で微分して\(dx\)をつけて、右辺を\(t\)で微分して\(dt\)をつければOKです。つまり、
\(2x+1=t\)より、
\(2 \cdot dx = 1 \cdot dt \)(←左辺は\(x\)で微分、右辺は\(t\)で微分してそれぞれ\(dx\)、\(dt\)をつける。)
\(2dx=dt\)
また、\(2x = t-1\)なので、
\(\displaystyle \int (2x+1)^5 \cdot 4x dx = \int (2x+1)^5 \cdot 2x \cdot 2 dx \)
\(\displaystyle \quad = \int t^5 (t-1) dt= \int (t^6 -t^5) dt\)
\(\displaystyle \quad = \frac{1}{7}t^7-\frac{1}{6}t^6+C\)(\(C\)は積分定数)
\(\displaystyle \quad = \frac{1}{42}t^6(6t-7)+C\)
\(\displaystyle \quad = \frac{1}{42}(2x+1)^6(12x-1)+C\)…(答)(←\(t\)は自分で勝手に置いた変数なので、元の\(x\)の式に戻しておく)
定積分なら\(x\)の式に戻す必要もない(積分区間も適切に置き換えて最後まで計算してしまうから)ですが、不定積分はまとめて\(x\)の式に戻しておきましょう。



積分結果やシグマ計算などは、どのくらいまとめるか…というのはなかなか基準が難しいです汗
例2.\(\displaystyle \int \frac{1}{e^x-e^{-x}}dx \)
例2の解答
(解答)
\(\displaystyle \int \frac{1}{e^x-e^{-x}}dx =\int \frac{e^x}{\{e^x\}^2-1}dx\)
なので、\(e^x=t\)と置きたくなりますよね。
先ほどと同様に、\(e^x=t\)の左辺を\(x\)で微分して\(dx\)をつけて、右辺を\(t\)で微分して\(dt\)をつけます。
\(e^xdx=dt\)
ラッキーなことに、\(\displaystyle \frac{e^x}{\{e^x\}^2-1}\)の分子に\(e^x\)があるので、これと\(dx\)を合わせて(\(e^xdx\)として)\(dt\)に置き換えます。
つまり、
\(\displaystyle \int \frac{1}{e^x-e^{-x}}dx =\int \frac{e^x}{\{e^x\}^2-1}dx\)
\(\displaystyle \quad = \int \frac{dt}{t^2-1}\)
と置き換えることができます。



ここからは部分分数分解という積分のテクニックの話になりますね。
\(\displaystyle \quad = \int \frac{dt}{t^2-1}=\int \frac{1}{(t-1)(t+1)}dt\)
\(\displaystyle \quad = \int \frac{1}{2} \left( \frac{1}{t-1}-\frac{1}{t+1} \right) dt\)(←部分分数分解)
\(\displaystyle \quad = \frac{1}{2} \{ \log{(t-1)}-\log{(t+1)} \} +C\)(\(C\)は積分定数)
\(\displaystyle \quad = \frac{1}{2} \log{\left( \frac{t-1}{t+1} \right) } +C\)
\(\displaystyle \quad = \frac{1}{2} \log{ \left( \frac{e^x-1}{e^x+1} \right) } +C\)…(答)
例3.\(\displaystyle \int_{0}^{1} \sqrt{1-x^2}dx \)
例3の解答
(解答)



この積分は、置き換えの決まり手があります!
結論、\(x = \sin{t}\)と置いてください!これで置換していきます。



今回は積分区間もあるので、そこまで置き換えていきます。
まず、積分区間は
\(\begin{array}{c|ccc}
x & 0 & \rightarrow & 1 \\
\hline
t & 0 & \rightarrow & \frac{\pi}{2}
\end{array}\)
となります。本当なら\(\sin{t}=0\)などをガチンコで解かないといけませんが、単位円をイメージしてもらえると考えやすいですね。
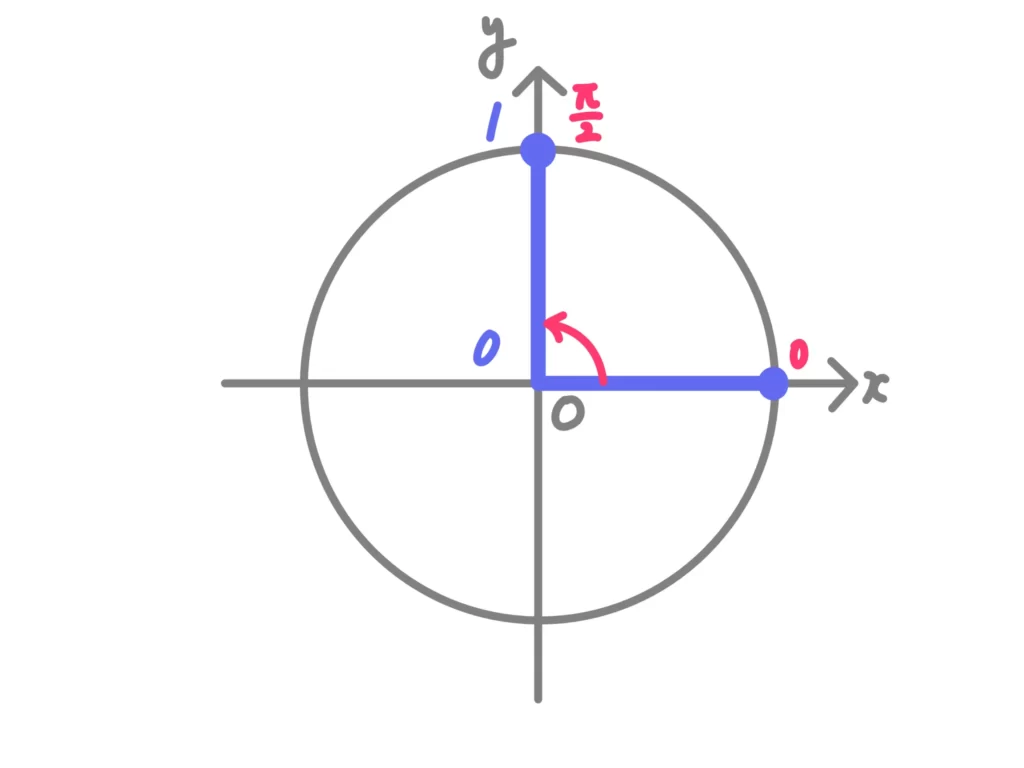




三角方程式や三角不等式は単位円をイメージしてビジュアルで解く方が早く正確に解けます!
また、\(x = \sin{t}\)より\(dx=\cos{t}dt\)。よって、
\(\displaystyle \int_{0}^{1} \sqrt{1-x^2}dx = \int_{\frac{\pi}{2}}^{0} \sqrt{1-\sin^2{t}}\cos{t}dt\)
\(\displaystyle \quad= \int_{0}^{\frac{\pi}{2}} \sqrt{\cos^2{t}}\cos{t}dt\)
\(\displaystyle \quad= \int_{0}^{\frac{\pi}{2}} |\cos{t}|\cos{t}dt\)
\(\displaystyle \quad= \int_{0}^{\frac{\pi}{2}} \cos^2{t}dt\)(←\(\displaystyle 0 \leq t \leq \frac{\pi}{2}\)のとき\(\cos{t} \geq 0\)だから、絶対値はそのまま外せる。)
\(\displaystyle \quad= \int_{0}^{\frac{\pi}{2}} \frac{1+\cos{2t}}{2}dt\)
\(\displaystyle \quad= \frac{1}{2} \left[ t + \frac{1}{2}\sin{2t} \right] _{0}^{\frac{\pi}{2}}\)
\(\displaystyle \quad= \frac{1}{2} \left\{ \left( \frac{\pi}{2} + 0 \right)- \left( 0 + 0 \right) \right\}=\frac{\pi}{4}\)…(答)
ちなみに、積分の中身を\(y=\sqrt{1-x^2}\)とおくと、\(x^2+y^2=1\)と変形できます。
つまり、\(y=\sqrt{1-x^2}\)は原点中心、半径1の円の上の半分を表す関数になります。
ですので、これを\(x:0 \rightarrow 1\)で積分する、ということは、円の\(\displaystyle \frac{1}{4}\)の面積を求めることになります。
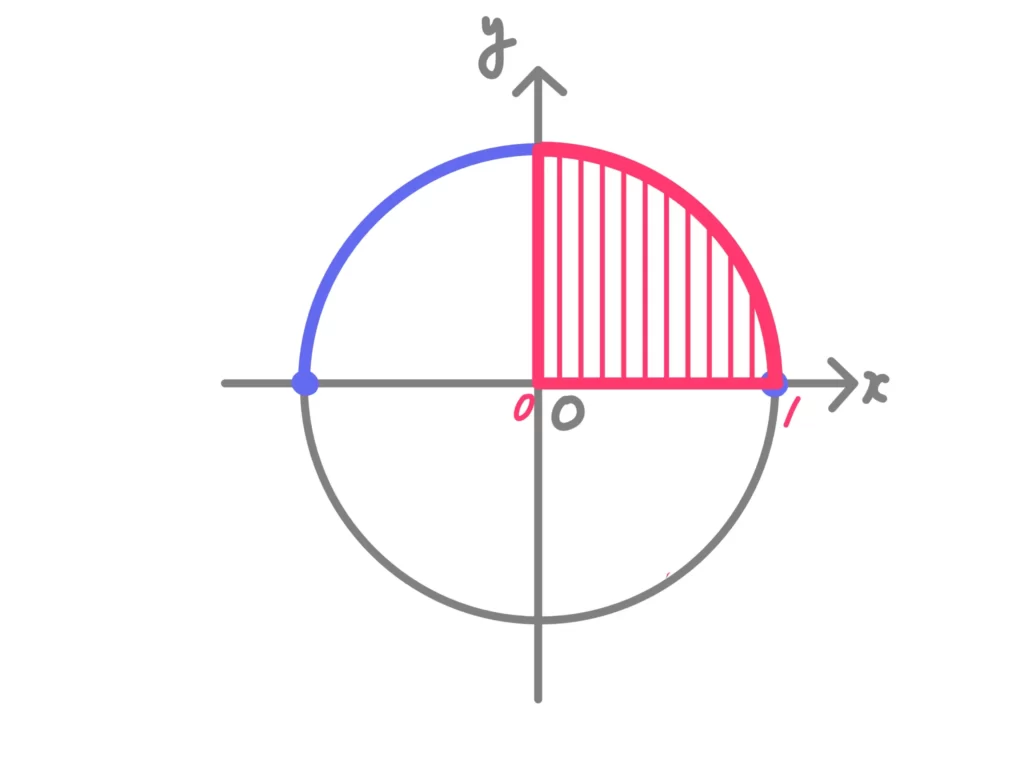

なので、\(\displaystyle \frac{1}{4} \cdot \pi 1^2 = \frac{\pi}{4}\)となります。
ちょっとした考察というか意見「g'(t)、dtについて」
dx=g'(t)dtについて
\(x = g(t)\)とおいたとき、\(\displaystyle \frac{dx}{dt} = g'(t)\)となり、\(dx = g'(t)gt\)となることは説明しましたが、この\(g'(t)\)について補足説明をしておきます。
\(g'(t)\)は関数\(x=g(t)\)のグラフの接線の傾きを表します。
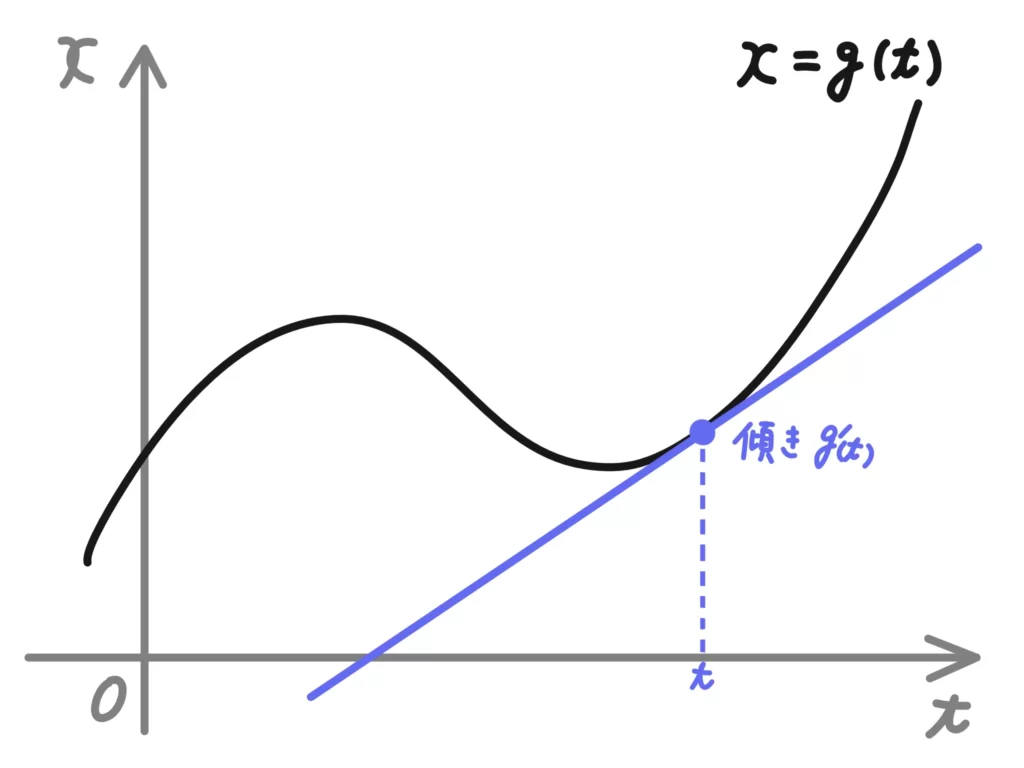




先ほどの例1の置き換えをもう一度考えてみましょう。
(解答では「こっちでもいいけど…」と言った方で考えてみる)
\(2x+1 = t\)とおくと、\(\displaystyle x = \frac{1}{2}t – \frac{1}{2} \)
\(\displaystyle dx = \frac{1}{2}dt\)
\(\displaystyle g'(t)=\frac{1}{2}\)意味は「\(t\)の増加量に対して\(x\)の増加量は\(\displaystyle \frac{1}{2}\)ですよ」ということで、置き換えたときの補正のようなものと思ってください。
一般的に\(x=g(t)\)と置いたとき、\(dx\)は\(g'(t)\)で補正できます。



下の図の右側は、増加が急な場合でも緩やかな場合でも\(g'(t)dt\)で\(dx\)を表せていることがわかります。
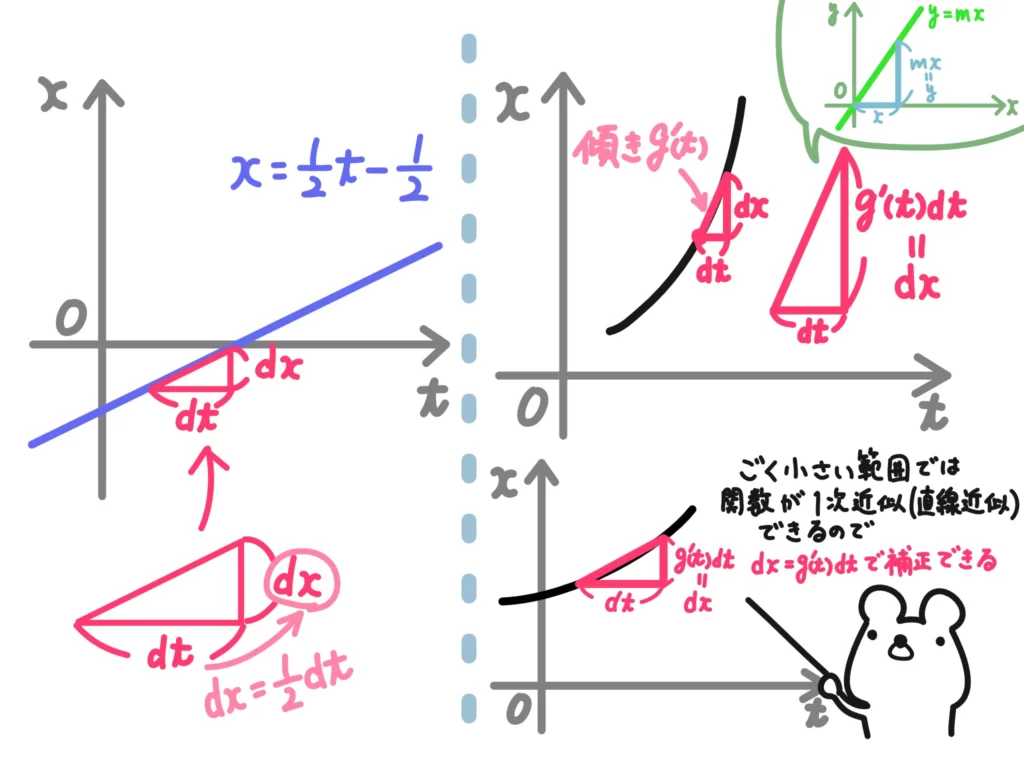

dtについて
これはおまけのような話ですが、
\(\displaystyle \frac{dx}{dt} = g'(t)\)
の\(\displaystyle \frac{dx}{dt} \)を分数のように扱って、
\( dx = g'(t)dt\)
としています。
これはあまり正確ではない、という意見もあります(なぜなら、\(\displaystyle \frac{dx}{dt} \)は無限小の意味を含む一つの記号だから。)が、個人的には問題ないんじゃないかと思います。
大学の数学(微分積分やベクトル解析)や物理の話ではよく使う表現方法ですし、\(\displaystyle \frac{dy}{dx}\)の\(dx\)や\(dy\)を分けたらダメなものと思っていると、あとあと困る気もします。



結局、どのサイトや参考書でも、言い訳のように「正確じゃないけどこうしていい」とか、何も言わずにしれっと使ってます。
「もういいんじゃね?」と思っちゃいますね笑。
まとめ
置換積分の注意点をまとめました。
置換積分は積分のテクニックとしてとても重要です。まずは確実に計算できるようにポイントを押さえて練習していきましょう。
また、余裕があれば\(dx\)と\(dt\)の関係も押さえておいてください。\(g'(t)\)のイメージを押さえておけば、今後、大学の積分で出てくる重積分のヤコビアンの理解にも役に立ちます。
おまけ



ここからは本文に関係ない宣伝です。
このブログはアフィリエイト(宣伝)に参加しているのですが、アフィリエイトの広告って、結構面白いものがあるんですよね。
中には「なにコレ!欲しい!」と思うようなものもあります。結構アフィリエイトの広告って眺めているだけでも面白いです。
私は結構多趣味でパソコン関係からスポーツ、アウトドア、料理…色々やります。そんな私が、有名なASPサイトである「A8.net」と「もしもアフィリエイト」の広告を全て見て「これは面白いな」と思ったものや、実際に利用しているサービスを紹介していきたいと思います!



ちょっと息抜きに見てみてください!
LINEスタンプ



新着スタンプなど、情報発信していきます。他にも「クマ」に関する情報が共有できたら、と思います!



インスタは結構更新頻度高いです!ちょっとしたマンガも描いてますのでぜひフォローお願いします。
ポイ活
ポイ活は地味にお得なのでコツコツとやってます。買い物したりミニゲームしたりでポイントを稼ぐのが好きな人にはオススメです!



ネットショッピングをよくする、という人にオススメ!いろんなネットショッピングがポイントがつつ対象になってます。結構貯まりますよ。



