PR
2025共通テスト「数学I A」徹底解説!【予備校の解説ではできない私見も】

この記事では2025年1月19日に行われた共通テスト「数学I A」の解説をしていきます!
 せんせ
せんせ手元に共通テストの問題を準備して読んでくださいね!
共通テスト数学ⅠA.第1問
[1]【数と式】
(1) \( (4x^2-1)b+16x-8 = (2x+1)(2x-1) + 8(2x-1) = (2x-1)(2bx+b+8) \)(答)
(2)(i) \( b=2 \)を代入。\( (2a+6)x^2+(5a+11)x-10=0 \)
\( 2(a+3)x^2 + (5a+11)x -10 =0\)
\( (2x+5) \{ (a+3)x-2 \} \)(答)…①
(ii) \( a=2 \sqrt{2}\)のとき、①の右側のカッコから、
\( (2 \sqrt{2}+3)x-2 =0\)
\(\displaystyle x = \frac{2}{2 \sqrt{2}+3}=6-4\sqrt{2} \)(答)
(iii) 「\(a=-3\)」→「\( (2x+5) \{ (a+3)x-2 \}=2x+5 = 0\)。よって解は\(\displaystyle x= -\frac{5}{2}\)のみ」◯
「解が\(\displaystyle x= -\frac{5}{2}\)のみのとき、重解の可能性もアリ。解の一つが\(\displaystyle x =\frac{2}{a+3}\)なので、コレを\(\displaystyle \frac{2}{a+3} = -\frac{5}{2} \)とすると\(\displaystyle a = -\frac{19}{5}\)」
よって「解が\(\displaystyle x= -\frac{5}{2}\)のみ」→「\(a=-3\)」✕。
したがって、十分条件であるが、必要条件ではない。(答)
係数に文字が入った式の因数分解はできてほしいですね。
必要十分も「重解の可能性がある」というところに気づけば解けるハズ。
[2]【図形と計量】
(1)
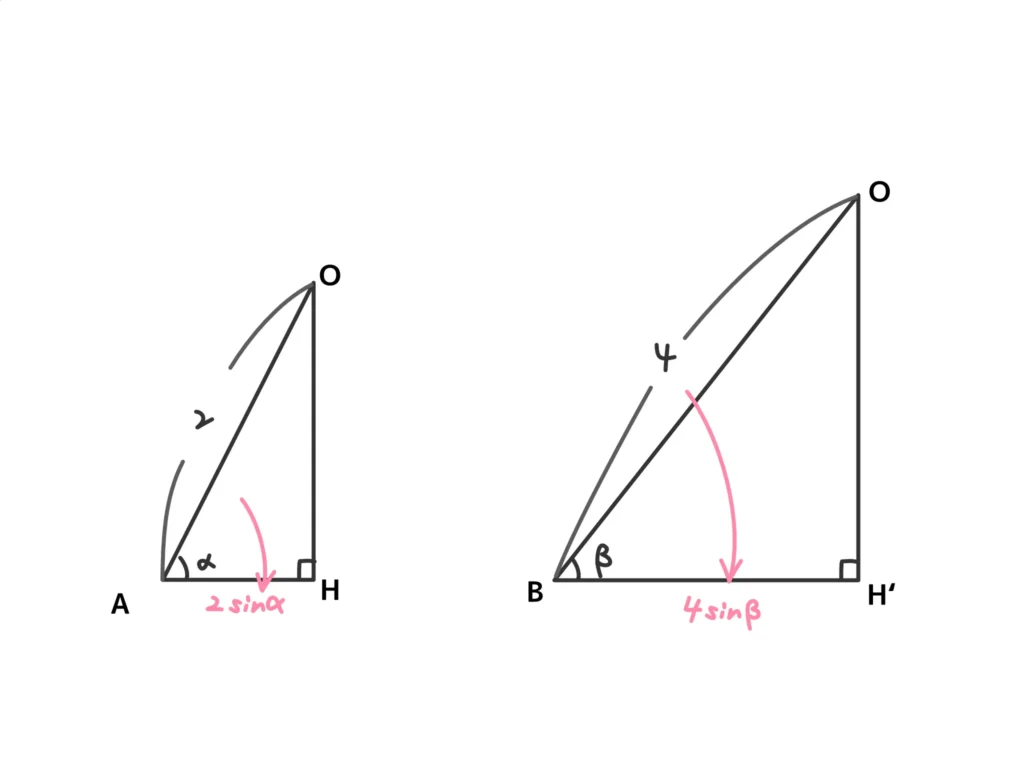

\( AH = 2 \sin {\alpha} \)(答)
\(PA = 2AH = 4 \sin{\alpha} \)(答)…①
\( PB = 2BH’ = 8 \sin {\beta} \)(答)…②
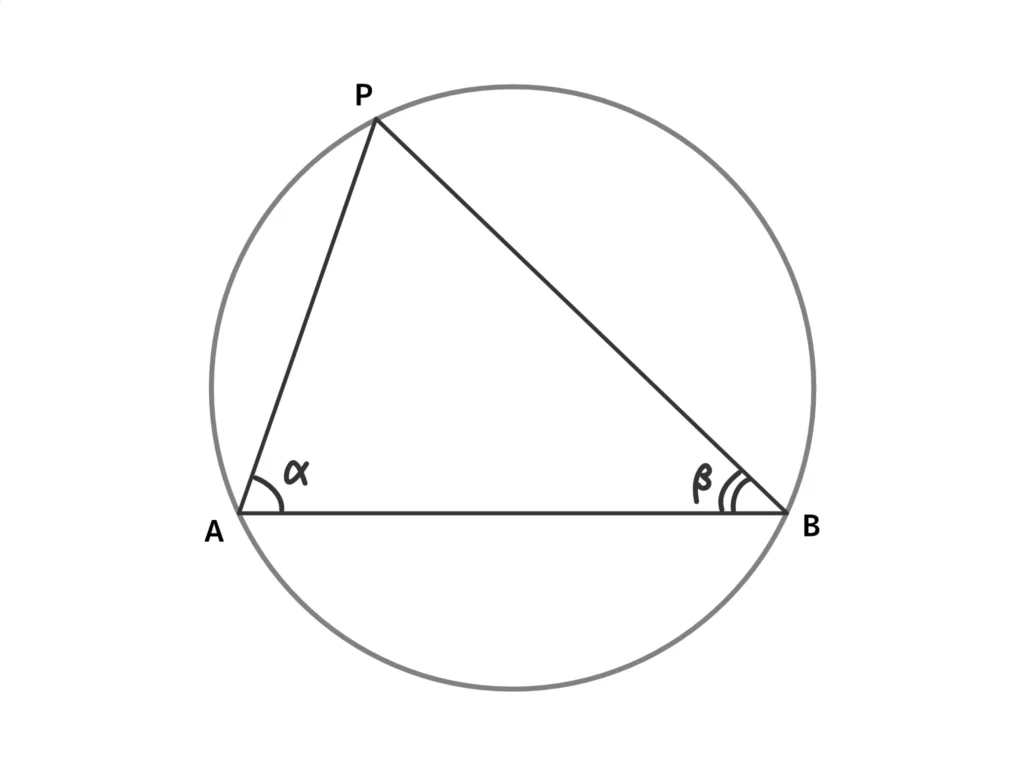

\(\displaystyle \frac{PA}{\sin {\beta}} = \frac{PB}{\sin {\alpha}} = 2R_1 \)(答)…③
①、②を代入すると、
\(\displaystyle \frac{4 \sin{\alpha}}{\sin {\beta}} = \frac{8 \sin {\beta}}{\sin {\alpha}} \)
\( \sin^2{\alpha} = 2 \sin^2{\beta} \)
\( \sin{\alpha} = \sqrt{2}\sin{\beta}\)(\( \sin{\alpha} > 0、\sin{\beta}>0 \) )(答)
よって(問題文から)\( PB=\sqrt{2}PA\)
③より \(\displaystyle \frac{PB}{\sin {\alpha}} = 2R_1 \)
\(\displaystyle \frac{\sqrt{2}PA}{\sin {\alpha}} = 2R_1 \)
\(\displaystyle \frac{\sqrt{2} \cdot 4\sin{\alpha}}{\sin {\alpha}} = 2R_1 \)(①より)
\( R_1 = 2 \sqrt{2} \)(答)
(2)
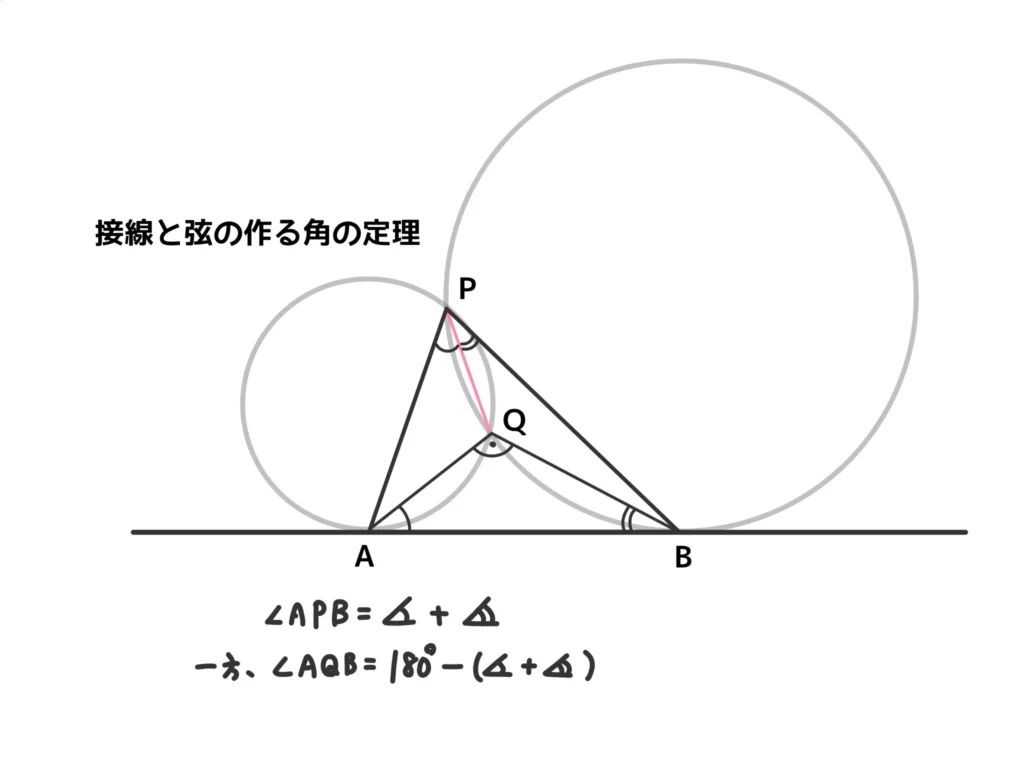

よって\( \angle{APB} = 180°-\angle{AQB}\)。
\( \sin{\angle{APB}} = \sin{\angle{AQB}} \)(答)
正弦定理から、\(R_1 = R_2\)となることもわかる。(答)
(3)
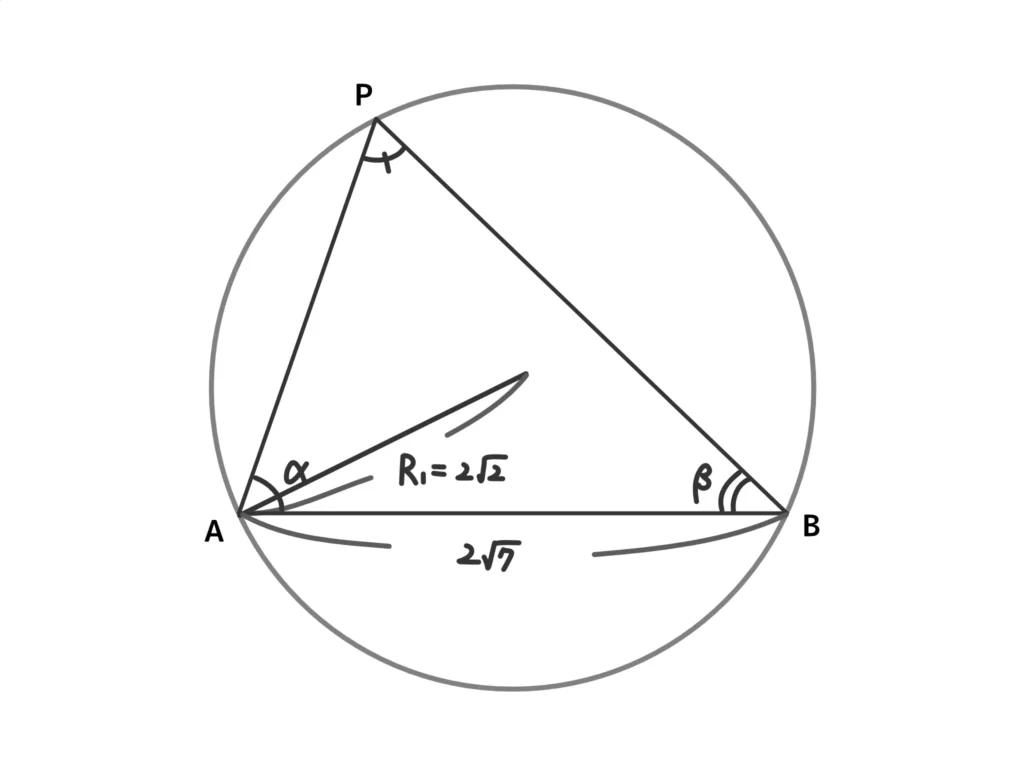

正弦定理から\(\displaystyle \frac{AB}{\sin{\angle{APB}}}=2R_1\)
\(\displaystyle \frac{2 \sqrt{7} }{\sin{\angle{APB}}}=4\sqrt{2} \)
\(\displaystyle \sin{\angle{APB}}=\frac{\sqrt{14}}{4} \)(答)
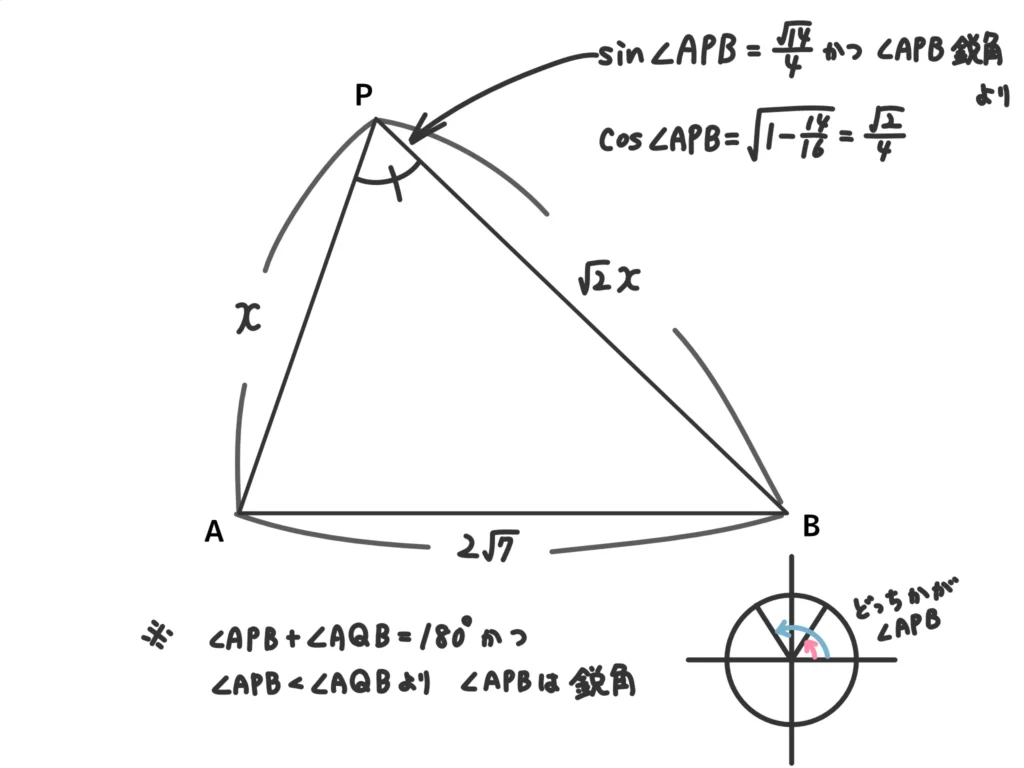

余弦定理より\(28 = x^2 + 2x^2 -2\cdot x \cdot \sqrt{2}x \cos{\angle{APB}} \)
\(\displaystyle 28 = 3x^2 -2\sqrt{2}\cdot \frac{\sqrt{2}}{4}x^2 \)
\(x^2 = 14\)
\(x = PA = \sqrt{14}\)(\(x>0\))(答)
正弦定理・余弦定理を使った標準的な問題ですが、関係式が散らかってるので何に何を代入するか…問題の流れに上手く乗る必要があります。
(2)は慌てずに図形的な性質を処理しましょう。こういう問題は根拠なく選ばないようにしましょう…大体考察が必要なことが多いです。
共通テスト数学ⅠA.第2問
[1]【2次関数】
(1)
点\( (0,1) \)を通るので、\( y = ax^2 + bx + c \)に代入して\(c=1\)(答)
点\(\displaystyle (-\frac{5}{2},0) \)、\(\displaystyle (\frac{1}{2},0) \)を通るので、
\(\displaystyle y = a \Big( x + \frac{5}{2} \Big)\Big( x – \frac{1}{2} \Big)\)とおける。
\(\displaystyle y = a \Big( x^2 +2x-\frac{5}{4} \Big)=a x^2 + 2a x – \frac{5}{4}a\)…①
定数項部分が1となるので、\(\displaystyle – \frac{5}{4}a=1\)
\(\displaystyle a=- \frac{4}{5}\)
①より\(\displaystyle y = -\frac{4}{5} x^2 – \frac{8}{5} x +1\)(答)
①より\(\displaystyle y = a \Big( x^2 +2x-\frac{5}{4} \Big) = a \Big\{ ( x + 1 )^2 -\frac{9}{4} \Big\} = a( x + 1 )^2 -\frac{9}{4}a\)
\(\displaystyle a=- \frac{4}{5}\)を代入して
\(\displaystyle y = -\frac{4}{5}( x + 1 )^2 +\frac{9}{5}\)
\(C_1\)の頂点の\(y\)座標は\(\displaystyle \frac{9}{5}\)(答)
対称性から\( C_2\)の頂点は\(y\)軸上にあり、かつ点\(\displaystyle (-\frac{3}{2},0) \)、\(\displaystyle (\frac{3}{2},0) \)を通るので、
\(\displaystyle y = k \Big( x + \frac{3}{2} \Big) \Big( x-\frac{3}{2} \Big) = k \Big( x^2-\frac{9}{4} \Big) \)とおける。
これが点\(\displaystyle (-1,\frac{9}{5}) \)を通るので、
\(\displaystyle \frac{9}{5} = k \Big( -\frac{5}{4} \Big) \)
\(\displaystyle k = -\frac{36}{25}\)
よって、\(C_2\)の頂点の\(y\)座標は\(\displaystyle \frac{81}{25}\)で、大きな噴水の高さは小さな噴水の高さのおよそ2倍。(答)
(2)
\(C’_2\)は\(y = lx^2 + 5\)とおける。
これが点\(\displaystyle (-1,\frac{9}{5}) \)を通るので、
\(\displaystyle \frac{9}{5} = l + 5 \)。よって、\(\displaystyle l= -\frac{16}{5} \)。
\(C’_2\)は\(\displaystyle y = -\frac{16}{5}x^2 + 5\)となるので、
\(\displaystyle -\frac{16}{5}x^2 + 5 = 0\)とすると、\(\displaystyle x = \pm \frac{5}{4} \)。
よって、\(P’_2\)は\(P_2\)より\(\displaystyle \frac{3}{2}-\frac{5}{4} = \frac{1}{4}\)だけ\(P_1\)の方にある。(答)
\(C_1\)を\(\displaystyle y = a \Big( x + \frac{5}{2} \Big)\Big( x – \frac{1}{2} \Big)\)とおいたり、\(C_2\)の頂点を求めるために、\(\displaystyle y = a \Big( x^2 +2x-\frac{5}{4} \Big) = a \Big\{ ( x + 1 )^2 -\frac{9}{4} \Big\} = a( x + 1 )^2 -\frac{9}{4}a\)を使うなど、細かい計算の工夫をすると時間短縮が見込める問題でした。
[2]【データの分析】
(1)(i)
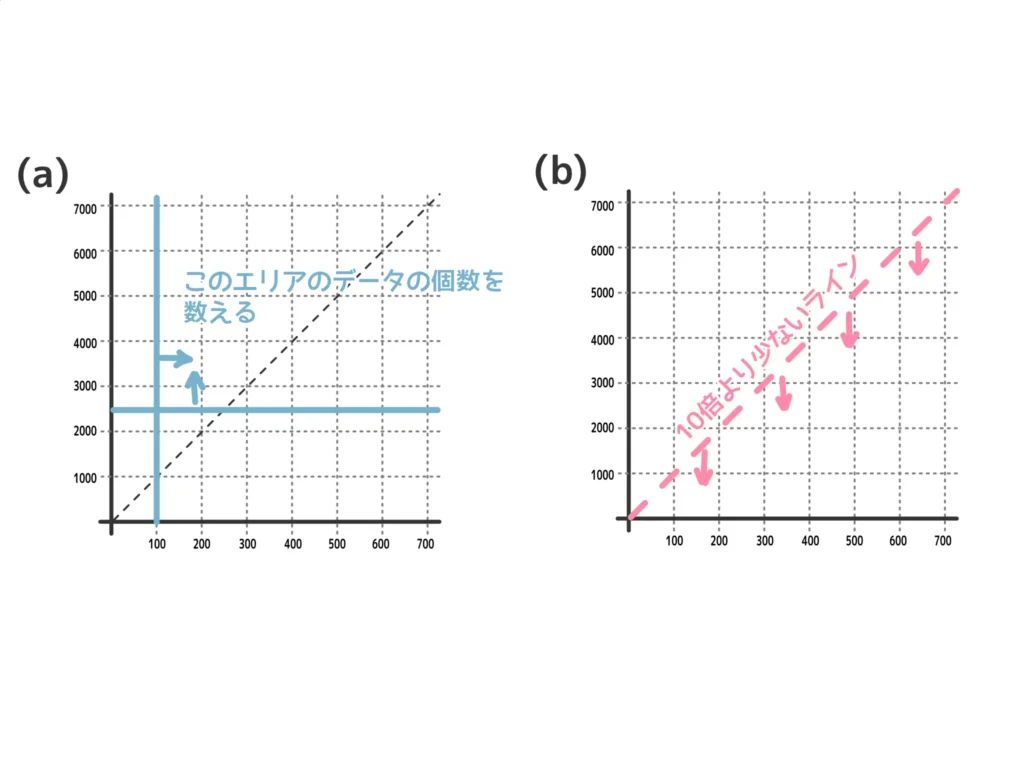

ということで、上の図と問題文の散布図を照らし合わせると(a)も(b)も正しいことがわかる。(答)
(ii) 第1四分位数はP12:351、第3四分位数はP36:1251なので、四分位範囲は\(1251-351 = 900\)。(答)
上方(下方には「外国人宿泊者数」で外れ値に該当するものがない)の外れ値のラインは\(1251 + 900 \times 1.5 = 2601\)。2601以上のデータであるP45、P46、P47は全部「外国人宿泊者数」も外れ値なので、両方外れ値である都道府県の数は3。(答)
(2)
\( z_i – \bar{z} = (x_i – \bar{x}) + (y_i – \bar{y}) \)より、\( (z_i – \bar{z})^2 = (x_i – \bar{x})^2 + (y_i – \bar{y})^2 +2(x_i – \bar{x})(y_i – \bar{y}) \)。
よって\(z\)の分散\(s_z^2\)は、
\(\displaystyle s_z^2 = \frac{1}{n}\sum{(x_i – \bar{x})^2}+ \frac{1}{n}\sum{(y_i – \bar{y})^2}+2 \frac{1}{n}\sum{(x_i – \bar{x})(y_i – \bar{y})}\)
\(s_z^2 = s_x^2+s_y^2+2s_{xy}\)(答)
相関係数と共分散の符号は一致する。今回は相関係数が正なので、共分散\(s_{xy}\)の符号も正。
よって、\(s_z^2 = s_x^2+s_y^2+2s_{xy}\)から\(s_z^2 – (s_x^2+s_y^2) = 2s_{xy} > 0\)、
\(s_z^2 > s_x^2+s_y^2\)(答)
(3)
23枚以上の割合を足すと、\( 2.4 + 0.9 + 0.5 + 0.4 + 0.1 =4.3\)(答)
ということで、
”「キャンペーンAの方が良い」と回答する割合と「キャンペーンBの方が良い」と回答する割合は等しい(=どちらのキャンペーンがいいか、という理由がない)”…(※)
とすると、「35枚中23枚以上(=35人中23人以上)」は4.3%の確率でしか起きない。5%より低いので、偶然23枚以上(23人以上)になったとは言い難い。
つまり、偶然ではなく理由があって「キャンペーンAの方がよい」と思っている人が多い。よって、(※)の仮説は誤っていると判断し、キャンペーンAの方がよいと思っている人が多いといえる。(答)
都道府県のデータの四分位数はよく出ます。47都道府県だったら「第1四分位数→12番目、第2四分位数(中央値)→24番目、第3四分位数→36番目」…は、まぁ覚えなくてもいいけど「四分位数に該当する数字がある&その数字を除くと四分位数と四分位数の間に11個のデータがある」くらいは知っておいてもいいかもしれません。
外れ値、仮説検定も新課程で初めて出てきましたが、オーソドックスな問題でした。ただ、仮説検定の問題の出し方は「この計算結果は何を言っているのか?」という論理的な説明力を聞いているのかな?と思いました。
共通テスト数学ⅠA.第3問【図形の性質】
(1)
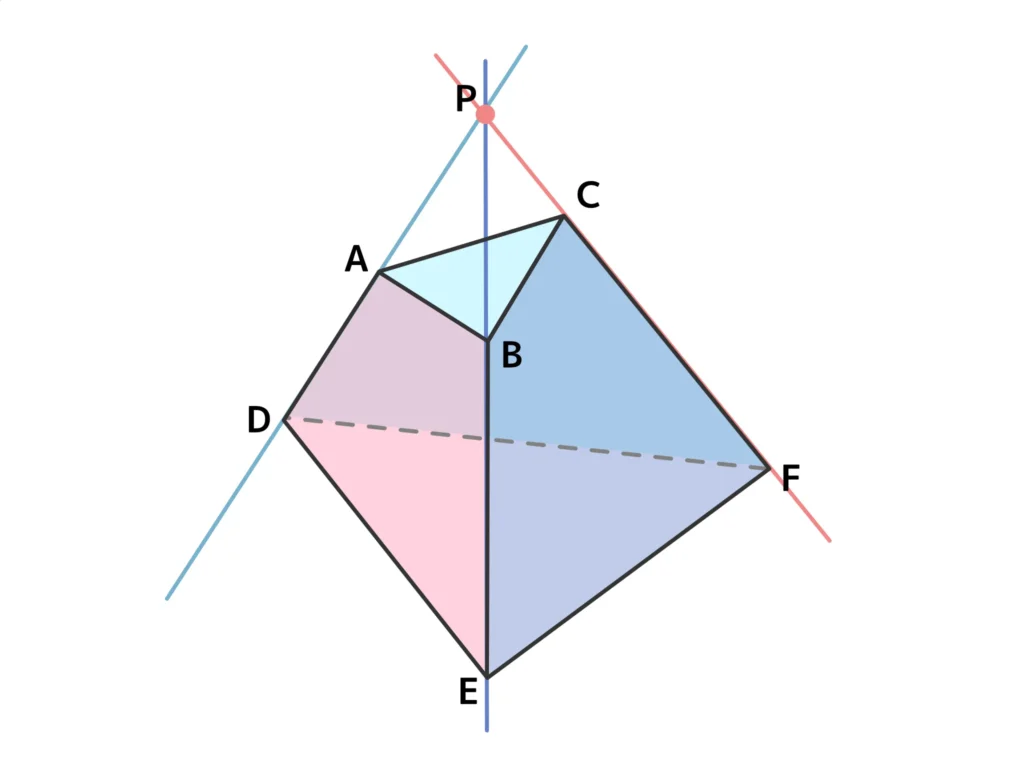

よって、直線ADは平面ABEDと平面ACFDとの交線、直線BEは平面ABEDと平面BCFEとの交線。(答)
(2)(i)
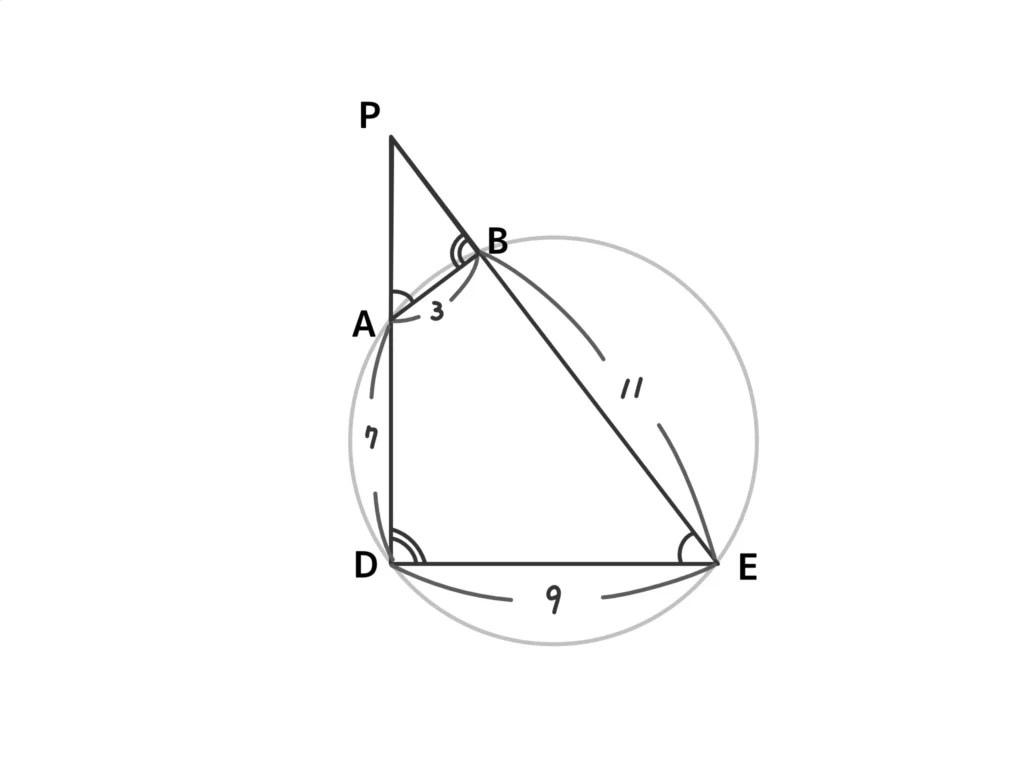

よって、相似比は1:3、\(3PA = PB + 11\)…①、\(3PB = PA + 7\)…②が成り立つ。(答)
①、②を連立して解くと、\(PA = 5\)、\(PB=4\)。(答)
(ii)
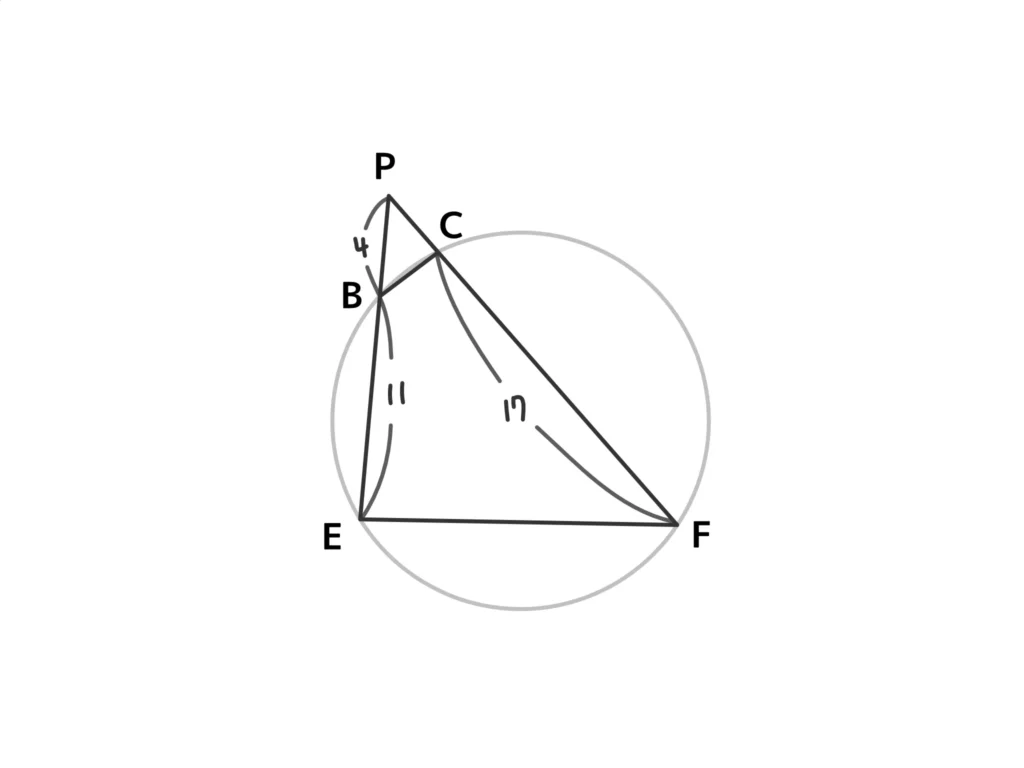

方べきの定理より、\(PC \cdot PF = PB \cdot PE \)
\( PC(PC+17) = 4 \cdot 15 \)
\(PC^2 + 17 PC – 2^2 \cdot 3 \cdot 5 = 0\)
\( (PC+20)(PC-3)=0 \)
\(PC>0\)より\(PC=3\)(答)
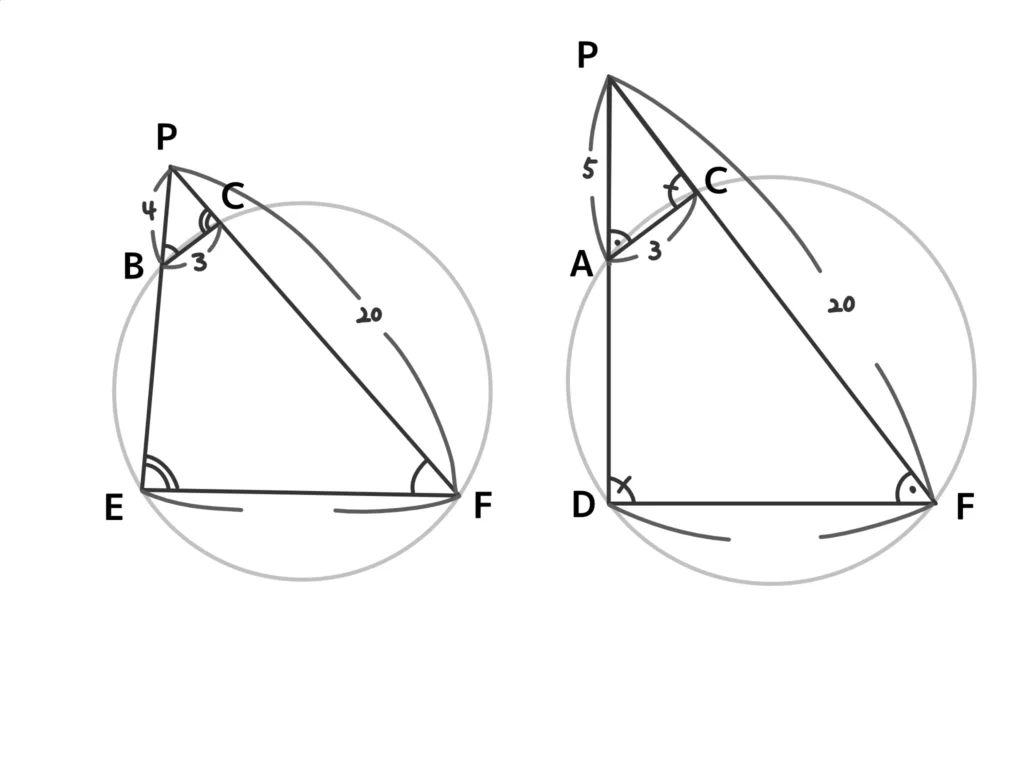

相似比を使って、\(\displaystyle EF = 3 \times \frac{20}{4} = 15\)、\(\displaystyle DF = 3 \times \frac{20}{5} = 12\)。(答)
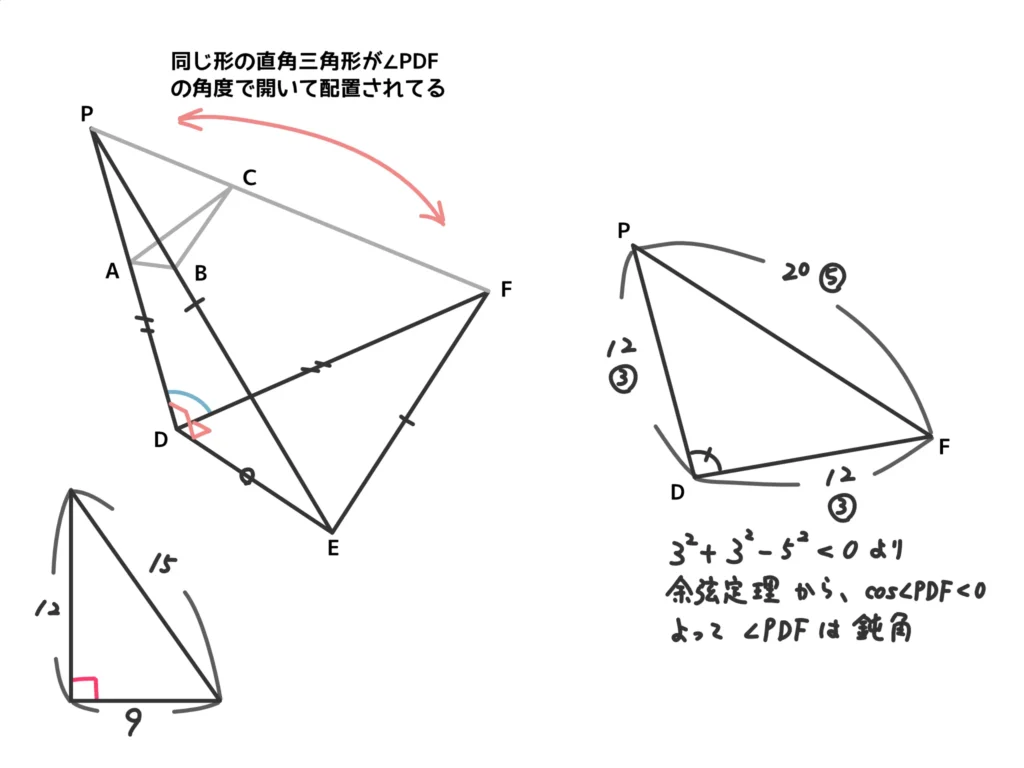

上の図のイメージから(a)平面ABEDと平面DEFは垂直である→偽、(b)直線DEは平面ACFDに垂直である→真、(c)直線ACと直線DEは垂直である→真。(答)
(補足)平面PDFと平面PED(平面ABED)、平面DEFは垂直。よって直線DE⊥平面PDF、直線AC(平面PDF上の直線ならどれでも)⊥直線DE。
立体図形なので慌てた人もいたかも…。計算はさほど難しくないが、空間上で相似を見つけたり直角を見つけたりしないといけないので「図形的な気づき」が必要な問題。
日頃から、特別な図形の関係や辺の値(直角三角形の三辺の数字の組など)に注意を払いながら問題を解くクセをつけましょう。
第4問【場合の数と確率】
(1) 1回目または2回目に当たりが出る確率は\(\displaystyle \frac{3}{16}+\frac{1}{8} = \frac{5}{16}\)。(答)
A:1回目に当たりが出る、B:2回目に当たりが出る(1回目当たらず2回目に当たる)、とすると、
「1回目、2回目ともに当たりがでない」→「Aでない、かつ、Bでない(\(\overline{A}\cap \overline{B}\))」→「AまたはB、でない(\(\overline{A \cup B}\))」
よって、\(\displaystyle 1-\Big( \frac{3}{16} + \frac{1}{8} \Big) = \frac{11}{16}\)。(答)
同様に考えると、1回も当たりが出ないのは「1回目が当たる、または、2回目が当たる、または、3回目が当たる」の余事象。
よって、\(\displaystyle 1-\Big( \frac{3}{16} + \frac{1}{8} + \frac{1}{16} \Big) = \frac{5}{8}\)。(答)
(2)(i) \(X=0\)となるのは「1回も当たらない確率」なので\(\displaystyle \frac{5}{8}\)。芋づる式に\(X=1200\)となるのは\(\displaystyle 1-\frac{5}{8} = \frac{3}{8}\)、
よって\(X\)の期待値は\(\displaystyle 1200 \cdot \frac{3}{8} = 450\)。(答)
(ii) 「主催者が得をする」→「参加料が妥当である」という言い方を押さえる。
「参加者の参加料が500円で、参加者が期待できる景品の期待値450円」という状況。よって、期待値が500円未満(450円)なので参加料500円という設定は妥当である。(答)
(3)(i) 「料金170円=1回目に当たる」「料金340円(\(170 \times 2 \))=2回目に当たる」「料金510円(\(170 \times 3 \))=3回目に当たる、または、3回目も外れる」
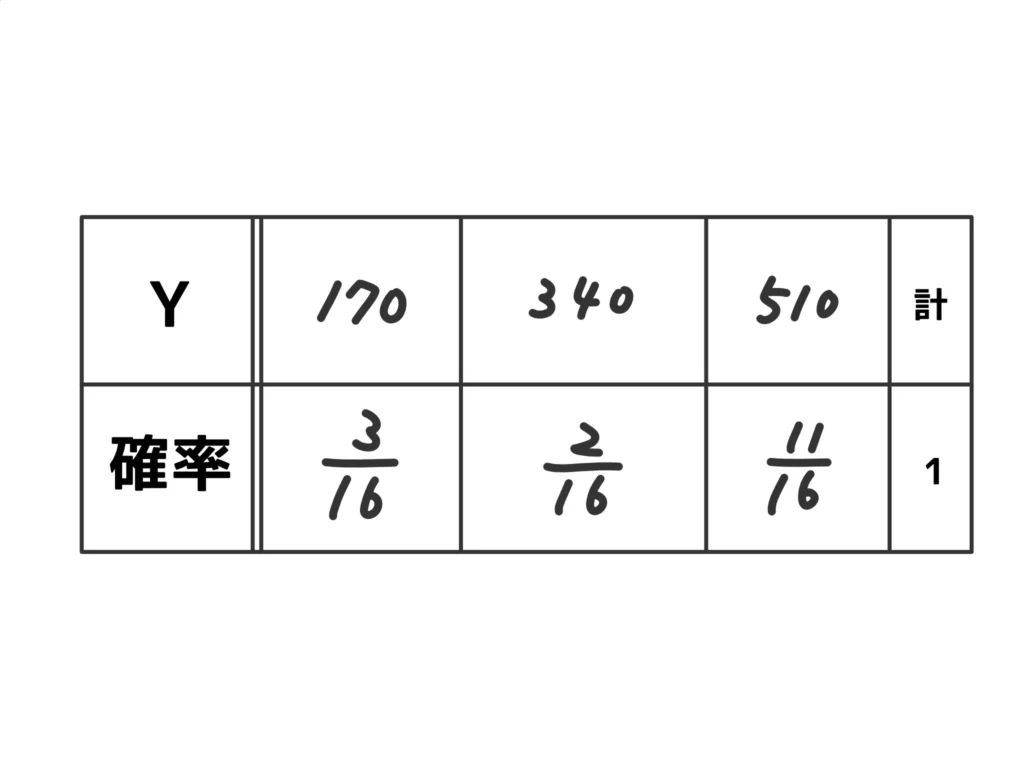

よって、\(\displaystyle \frac{170 \times 3 + 340 \times 2 + 510 \times 11}{16}=\frac{170(3+4+33)}{16} = 425 \)。…(※)(答)
(ii) 「参加者が期待できる景品の期待値450円」。一方(3)(i)での「参加者の参加料の期待値は425円」。なので、「参加者が期待できる景品の期待値450円は参加者の参加料の期待値425円以上」。(答)
よって、主催者が損をするので、この参加料の設定は妥当ではない。(答)
くじを引く前に払う料金\(a\)円とすると、(※)の\(170 \rightarrow a\)とすればよいので、
\(\displaystyle \frac{40}{16}a = \frac{5}{2}a\)。
これが、景品の期待値450円より大きければ主催者が得をする(妥当である)ので、
\(\displaystyle \frac{5}{2}a > 450\)
\( a > 180\)。(答)
最初の設定で、どこまでの確率が与えられているのか?がちょっとわかりにくいかもしれません。「1回目が当たらず、かつ2回目が当たる(=要は2回目に当たる)」で確率\(\displaystyle \frac{1}{8}\)です。確率を考える上で重要な「かつ」という言葉が、この段階では必要ありません。「2回目に当たる確率」と読めればOKです。
計算自体はあまり難しくありませんが、この問題も「妥当・妥当でない」という言葉で論理的な説明力を聞いているのかな?と思いました。
2025共通テスト「数学I A」解説まとめ
2025年共通テスト「数学IA」の解説でした。
新課程で初めての共通テストだったので、やや簡単だったかな、という感じですが、今後の共通テストの方針が見えるメッセージ性のある問題が多かった印象です。





