PR
箱ひげ図のかき方【四分位数や四分位範囲と箱ひげ図の関係もわかる!】

箱ひげ図は中学で習うのですが、これが便利なようで意外と何をしているのかわかりにくいです。
この記事では、箱ひげ図のかき方を説明しながら、箱ひげ図のデータの読み取り方について深堀りしていきます。
箱ひげ図とは
 たろぅ
たろぅいやだ!絶対に捨てない!



いや…まぁ、そこまで言うならいいけど…。でも邪魔じゃないの?



フィギュアは箱!箱命なのよ!箱がないとフィギュアの価値が無くなる、って言っても過言じゃない!



(男ってめんどくせぇわ…)


ということで、箱ひげ図です。
箱ひげ図…なんで「箱」と「ひげ」があるのか、わかりますか?



んー…ひげがあった方が大人っぽいから?
全然違います。ちゃんと「箱」と「ひげ」には理由があるんです。



箱ひげ図の形の意味を知るには実際にかいてみるのが一番ですね。
箱ひげ図と四分位数の関係
箱ひげ図をかくには、データの四分位数を求める必要があります。



(四分位数…?習ったような…)
四分位数とは、データを小さい順に並べたときに、そのデータ全体の特徴を表す3つの数のことです。この3つの数によって、データが4つのエリアに分けられます。



データを4つに分割する数だから「四分位数」ですね。
具体例を使いながら、四分位数を求めてみましょう!
例.10人に数学のテスト(100点満点)をしたら、次の表のような結果になった。なお、データは小さい順に並んでいる。
| 点数 | 30 | 35 | 37 | 62 | 68 | 78 | 83 | 84 | 91 | 97 |
|---|
このときの四分位数を求めてみましょう。
① まずは全体のデータを半分に分けます。このとき、小さい順に並んだ真ん中のデータの値を中央値(または第2四分位数)といいます。


10個のデータを半分に分けるので真ん中のデータの値がありません。こういうときは真ん中の2つのデータの平均をとります。
今回、真ん中に並んでいる2つのデータは68と78なので、平均を計算すると\(\displaystyle \frac{68+78}{2} = 73\)。よって、中央値(第2四分位数)は73となります。
② 中央値によって、全体のデータが2つに分けられます。このとき、中央値より小さいデータ達を下位のデータ、中央値より大きいデータ達を上位のデータ、といいます。
全体のデータの個数が奇数で、中央値=真ん中のデータの値となる場合、その真ん中のデータは下位のデータにも上位のデータにも入らないことに注意しましょう。


簡単に言うと、同じように、この「下位のデータの中央値」と「上位のデータの中央値」を求めればOKです。「下位のデータの中央値」を第1四分位数、「上位のデータの中央値」を第3四分位数といいます。
| 下位のデータの点数 | 30 | 35 | 37 | 62 | 68 |
|---|
| 上位のデータの点数 | 78 | 83 | 84 | 91 | 97 |
|---|
下位のデータの中央値は37(これが第1四分位数)、上位のデータの中央値は84(これが第3四分位数)です。


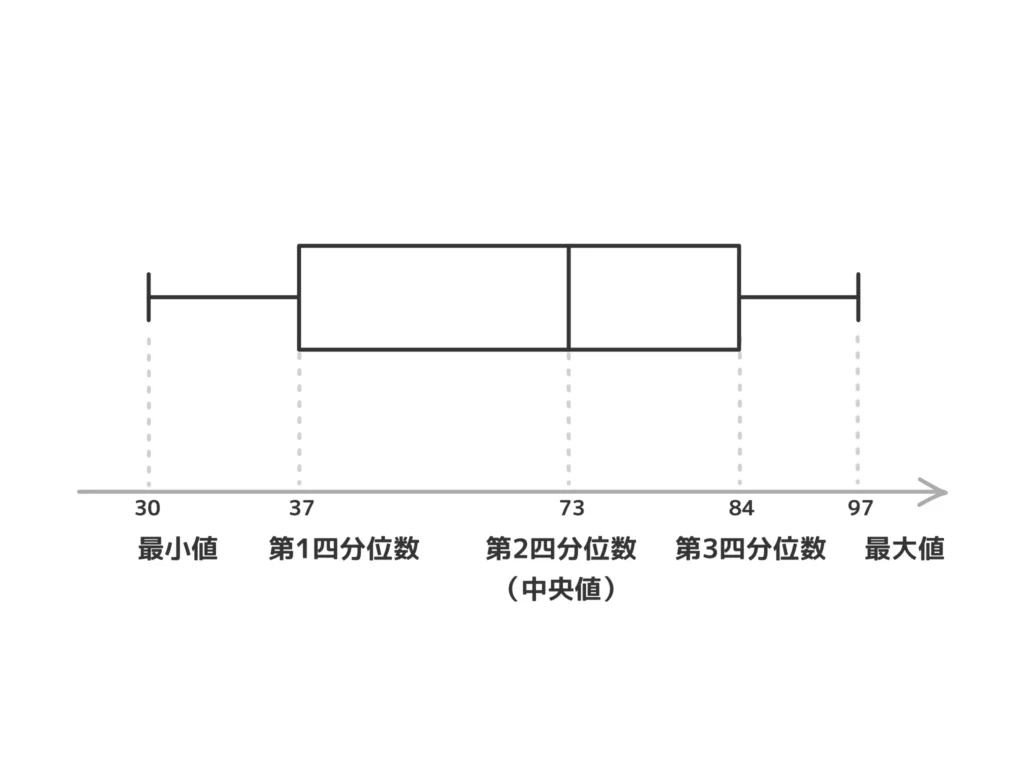
以上、まとめると第1四分位数は37、中央値(第2四分位数)は73、第3四分位数は84となります。



これで四分位数が求められました。
箱ひげ図のかき方
正直、四分位数を求めれば箱ひげ図はかけたも同然です。



次のようにデータを箱ひげ図におこしていきます。
- データの最小値→左ひげの端
- 第1四分位数→箱の左辺
- (中央値)第2四分位数→箱の真ん中
- 第3四分位数→箱の右辺
- データの最大値→右ひげの端




んー…で?
問題は箱ひげ図の読み取りです。
なぜこんな図を作るのか?箱ひげ図の特徴や、読み取れることについて解説していきます。
箱ひげ図の特徴と四分位範囲の関係
箱ひげ図には次のような特徴があります。
① ひげ部分と箱の半分には、それぞれ全てのデータの約1/4ずつが入っています。「約」と言っているのは、四分位数にちょうどデータの値が乗る場合、そのデータは除かれるからです。
② 箱ひげ図が広がっている場合は全てのデータの散らばりが大きく、狭い場合は全てのデータの散らばりが小さいです。
③ 試験問題的には箱もひげも同じような扱いですが、実際のデータ的には箱部分が重要です。なぜかというと、この箱の長さが「真ん中を基準に全てのデータのちょうど半分」が入っているからです。つまり、箱は全てのデータの特徴をよく表している部分になります。



ひげ部分には外れ値が含まれていることもあるので、全てのデータの大まかな特徴を表しているのは箱部分、となるわけですね。
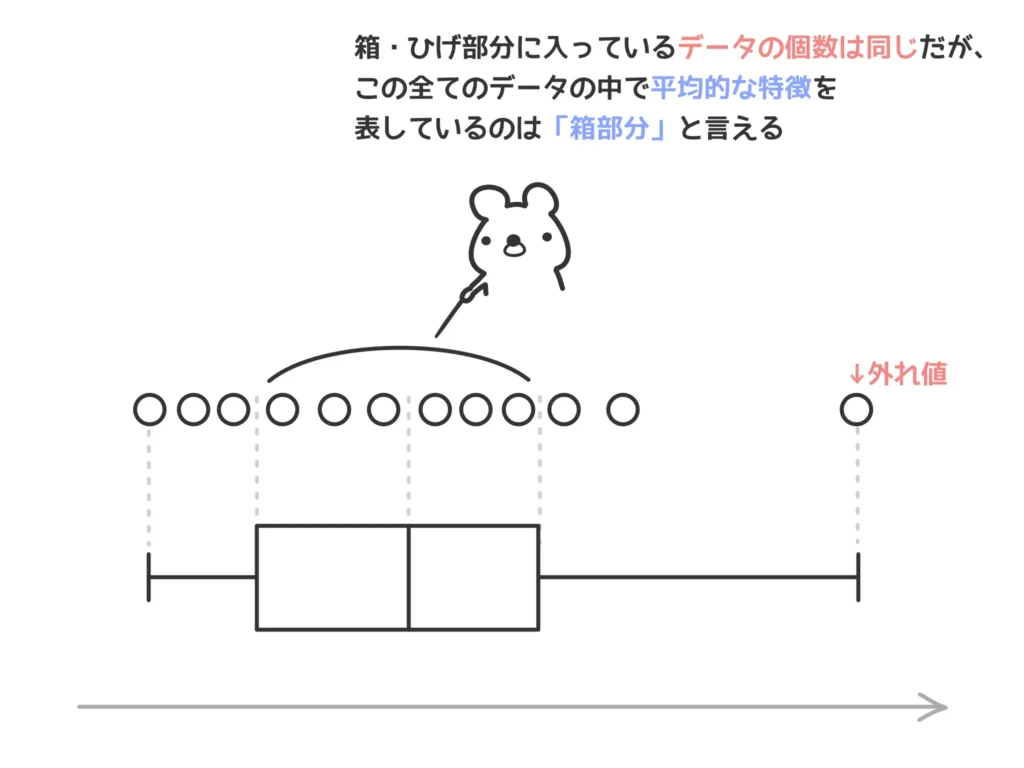

ちなみに、箱の長さは(第3四分位数)ー(第1四分位数)で計算できますが、これがちょうど四分位範囲になります。「箱の長さ=四分位範囲」は真ん中の半分のデータ(その全データの特徴的な部分)がどれだけ散らばっているか?を表します。
④ このような特徴を踏まえて、全てのデータのセットを1つの箱ひげ図であらわすことができるので、複数あるデータのセットを比較しやすいです。
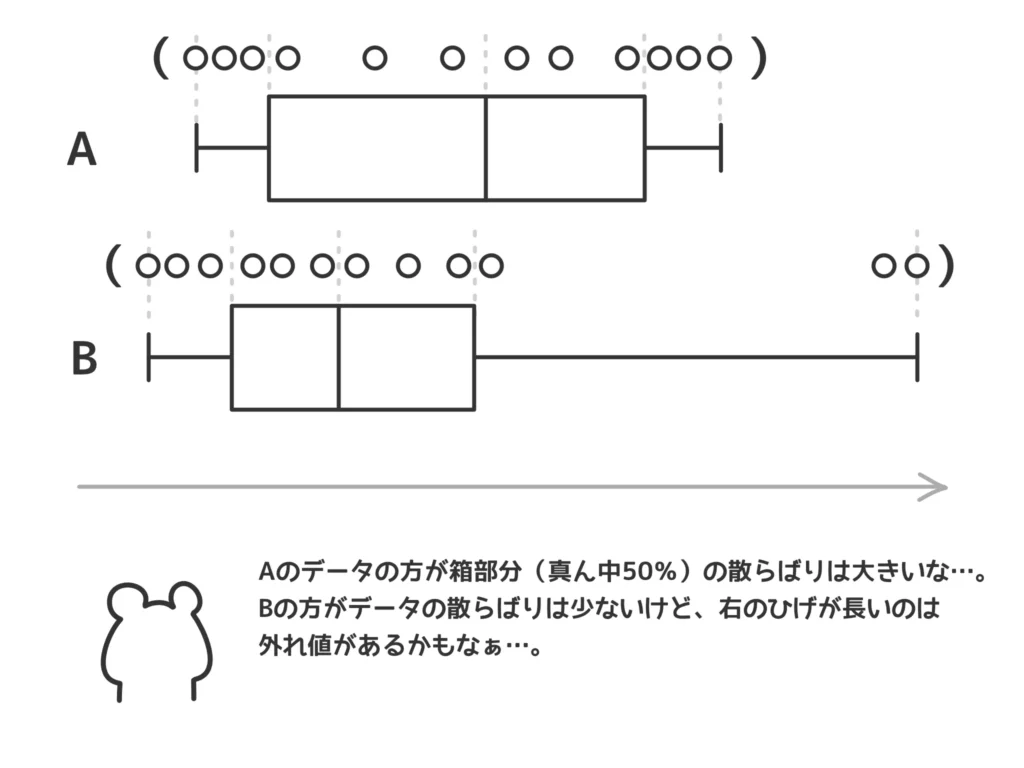

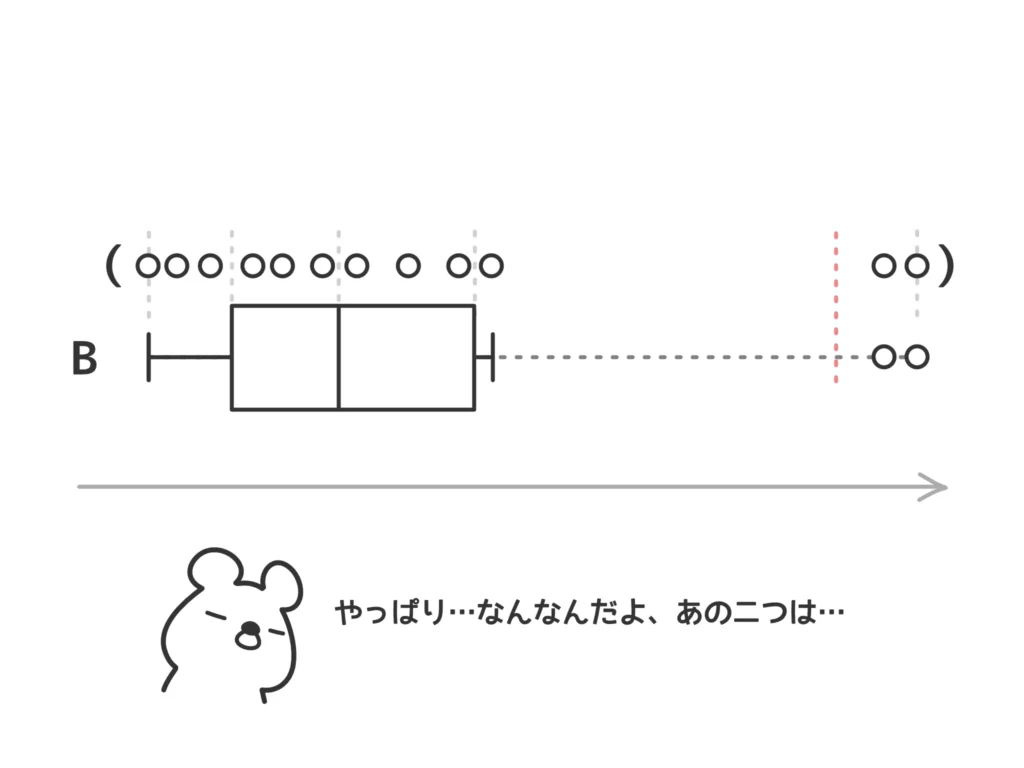
ただし、細かい中のデータの様子は想像するしかありません…。もちろんその想像は外れることもあります。図の「()」で囲んでいるデータ◯は実際には見えません。
④ ひげには外れ値が含まれることも意識しておいて下さい。試験問題としては見たことはありませんが、Excelで箱ひげ図を作ったりした場合、外れ値を除いたデータ達でひげ部分を作ることがあります。箱ひげ図の話をしているときの外れ値は、箱の1.5倍の長さ以上にあるもの、となります。

【番外編】
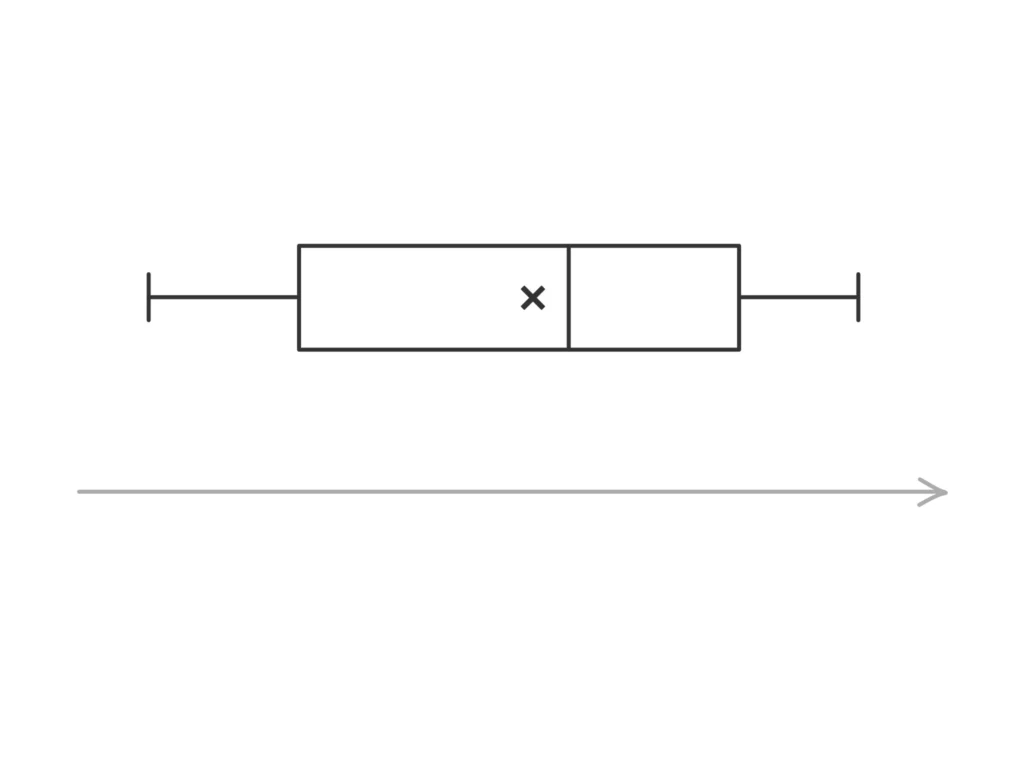
・平均値を「✕」で箱ひげ図上に表示することがあります。

箱ひげ図の読み取り練習
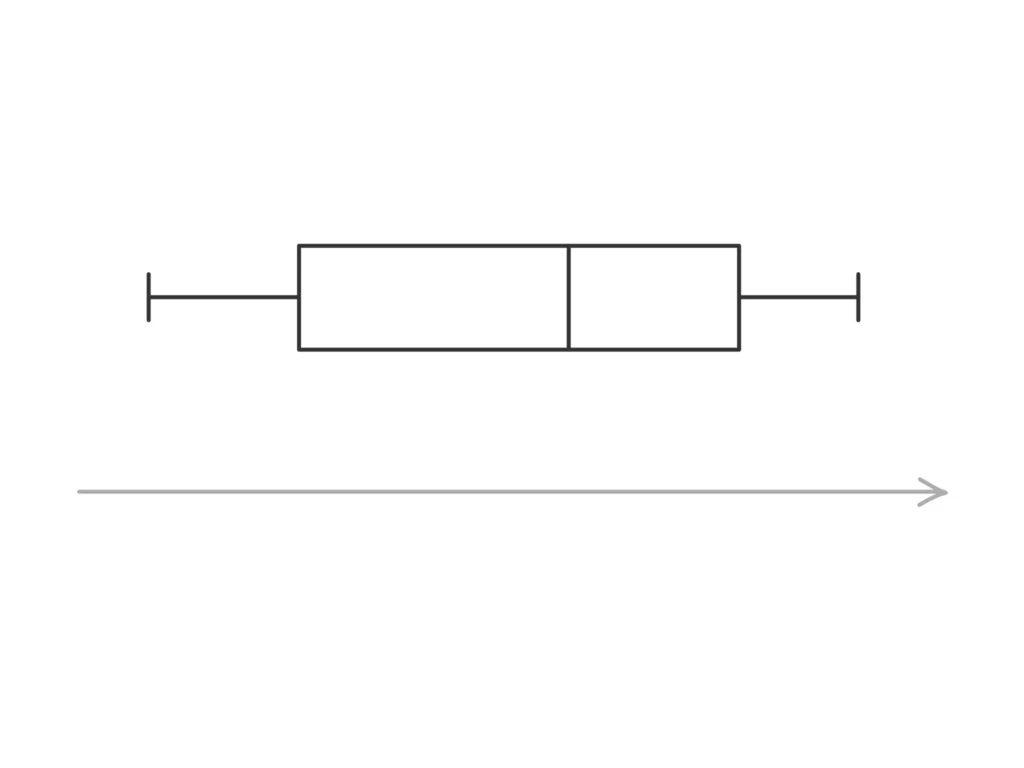

上の箱ひげ図が次のデータを表しているとき、「箱に入っているデータの個数」と「横軸の単位」と「最大値として予想されるおよその値」を求めよ。
(1) 47都道府県別の人口を箱ひげ図にした。
(2) 40人1クラスの高校生の生徒が50m走のタイムを測った。1学年10クラスの各クラスの平均タイムを箱ひげ図にした。
(3) 全国で朝食でご飯を食べる割合を「10代」「20代」…「50代」「60代以上」と年齢別にまとめて箱ひげ図にした。
答え
(1) 23個(全データ47個)、「人」、約1400万(東京都)。
(2) 4個(全データ10個)、「秒」、約8秒(高3男子の50m走平均が約7.3秒)。
(3) 2個(全データ6個)、「%」、65%(2006年NHK調べで64%)。



えー…最後の「最大値として予想されるおよその値」は当たらなくてOKです。あくまで予想で正しい値ではないからです。参考まで、ということで。ただし、「このようなデータを調べてるんだからこのくらいじゃないか?」くらいの予想ができると箱ひげ図の読み取りがしやすくなります。
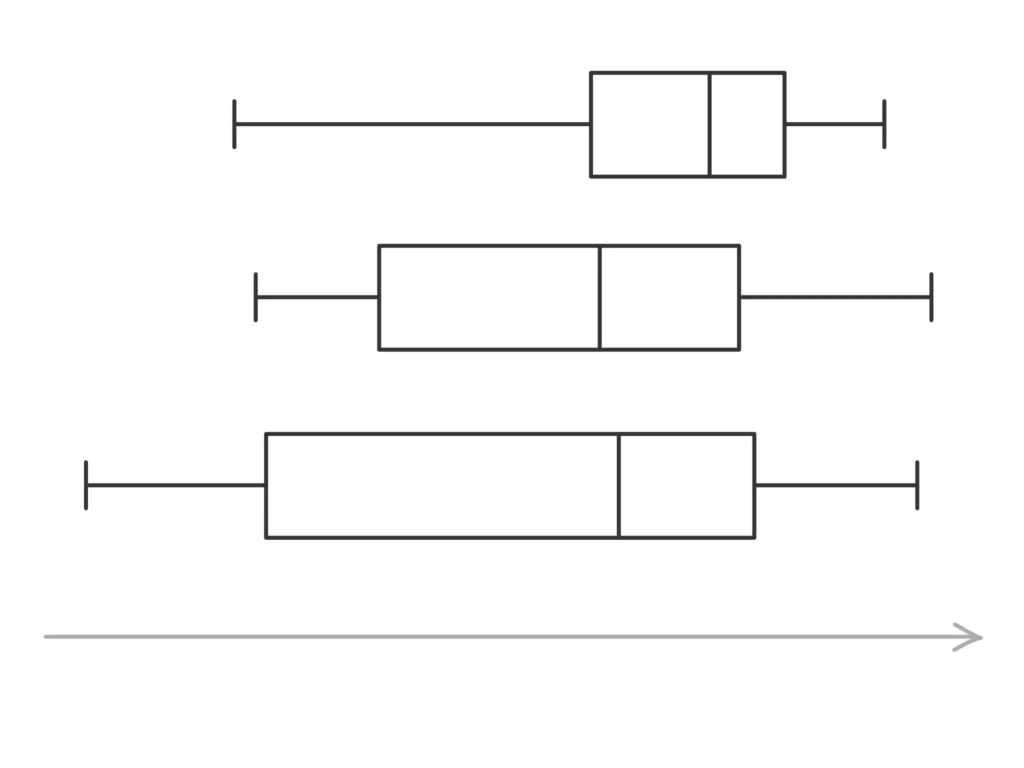

上の箱ひげ図が次のデータを表しているとき、「箱に入っているデータの個数」と「それぞれの箱ひげ図が表すデータの名前」「横軸の単位」と「最大値として予想されるおよその値」を求めよ。
(1) 全世界における、平均身長の高い国ベスト10を過去3年分箱ひげ図にした。
(2) 料理が趣味のはなこさんは世界でどれだけの肉が消費されているのか知りたくなった。そこで全世界197カ国の牛肉、豚肉、鳥肉の年間消費量(1人あたり)を調べてそれぞれの箱ひげ図にまとめた。
(3) 各都道府県に平均してどれだけの学校があるのか?という疑問をもったたろうくんは、各都道府県における小学校、中学校、高校の数をまとめた。しかし、各都道府県によって学校数にばらつきが大きく外れ値もあり、適正な情報が得られないと判断したので、上位25%のデータと下位25%のデータを除いた(第1四分位数、第2四分位数に該当するデータも除いた)各校種別のデータにまとめ直し、箱ひげ図にした。
答え
(1) 4個(全データ10個)、「2021年・2022年・2023年」(基準の年による)、「cm」or「m」、184cm(オランダ男性の平均。高い!)
(2) 99個(全データ197個)、「牛肉・豚肉・鶏肉」、「kg」(基準による)、40kg(香港が肉の消費量が多い。中でも豚肉は年間約38.4kg/1人(2002年)。)
(3) 11個(全データ23個)、「小学校・中学校・高校」、「校」、525校(ちょっと古いデータですが平成23、24の新潟の小学校の数。ちなみにこの23個のデータ外ですが、小学校数最多は東京の1363校です。)



上の問題と同様、最後の「最大値として予想されるおよその値」は当たらなくてOKです。3つの箱ひげ図のデータの名前や、単位も本当は細かい設定が必要ですが、あくまで一般的な、という認識で解いて下さい。肉の消費量とか学校の数とか…知りませんよね笑。
箱ひげ図のかき方まとめ
箱ひげ図のかき方のまとめでした。
箱ひげ図は
- データセットの四分位数を元に作られる。なので、データセットの散らばり方とデータの個数がどの範囲にどの程度含まれているか?がわかりやすい。
- 複数のデータセットの比較がしやすい。
- 中の細かい様子はわからない。
という特徴があります。
ですが、実際にパッと箱ひげ図が与えられると、どんなデータがどの程度含まれているか?がわかりにくかったりもします。



まずはデータセットが「何個あるのか?」「どんな値をデータとしてもっているのか?」を確認しましょう。