PR
常用対数は実は便利!?わかりにくい常用対数の正体を見抜く

常用対数は、教科書では「桁数を求める」くらいでしか利用しません。
常用対数表なんかも出てきますし、なんだかよくわからないうちに桁数を求める、という操作だけ教わります。
ですが、常用対数を利用すれば、もっと色々なことがわかるんです!
この記事では、あまり深掘りされない常用対数について丁寧に解説していきます。
 せんせ
せんせ常用対数の本質的な意味を理解してもらえば、桁数を求めるだけでない、本当の便利さがわかりますよ!
常用対数とは?



やばい…この後、映画に行かないといけないのに、手持ちのお金がない…。
あ!はなこさーん!お金貸して!
2000円貸して!



いいよー。
そのかわり複利計算でトイチ(10日で1割の利息がつく)ね。



(複利計算?)なんでもいいよ、とりあえず貸して!映画始まっちゃう!



はい、どーぞ。
1年後…。



しばらく前に貸した2000円そろそろ返して。1年前だけど…まぁ360日分の利息つけて返してくれればいいよ。



え…いくら返せばいいんだろ?
ということで(←?)、今回のテーマは常用対数です。
常用対数は底が10の対数のことで、「これを使うと何かと便利」という性質がありますが、実際のところ何が便利なのか?がわかりにくい…というかそこまで授業で解説しない、というか…。



常用対数の何が便利か?を解説していきます!
常用対数
底10の対数のことを常用対数、といいます。
\( \log_{10}{a}\)
大きい・小さい数の表し方
結論から言うと、常用対数はものすごく大きな数とか、ものすごく小さな数(0に近い、という意味で)の値を求めたり、評価をするときに便利な道具です。



ということで、まずは大きな数とか小さな数の表現の仕方を押さえていきます。
大きな数や小さな数は、あまり細かい話をしても大勢に影響がないという特徴があります。
例えば、一時流行った「世の中にいる男性は35億」というのは1千万以下の数字を完全に無視しちゃってますよね。
これは、アタマの「35」という数字と「億」という規模がわかれば大体の数の様子が掴めるからです。
ということで、大きい数や小さい数は次のような形で表現することがあります。
大きい数や小さい数の表現方法
\( a \times 10^n\)
ただし、\(1 \leq a < 10\)、\(n\)は整数とする。
例1.月までの距離約38万km(=380000km)。上の表現方法で表すと、
\(3.8 \times 10^5 \)(km)



\(38 \times 10^4 \)と書かずに\(3.8 \times 10^5 \)として\(1 \leq 3.8 < 10\)に押さえているところがポイントですね。
38は10を超えているので、\(3.8\times10\)として\(10^n\)に吸収させた方が統一した表現ができます。
例2.酸素分子の大きさ約0.35nm(ナノメートル) (=0.00000035m)。上の表現方法でm(メートル)に直すと、
\(3.5 \times 10^{-7}\)(m)
こんな感じで、実際に「0」を書くのが大変な数でも「\(10^n\)」の形にすることで、わかりやすくシンプルに、また「3.8」や「3.5」で大体の大きさを表現することができます。当然小数点以下の数を増やせば精度が上がっていきます。
理科ではよく目にする数の表現方法ですね。



…で?常用対数がどこに出てくるの?
常用対数を上手く使う
よくある常用対数の例で勉強
よくある常用対数の問題で、こういうものがあります。
問.\(2^{100}\)は何桁の数か?ただし、\(\log_{10}{2}=0.3010\)を使ってよい。



この問題を深掘りしながら、常用対数の正体とその便利さを理解してもらいましょう!
(解答)
まずは普通に解いていきましょう。
\(2^{100}\)の常用対数をとります。
\(\log_{10}{2^{100}}=100\log_{10}{2}\)
\(\quad = 100 \times 0.3010 = 30.10\)
\(30 < \log_{10}{2^{100}} < 31\)より
\(10^{30} < 2^{100} < 10^{31}\)
なので、\(2^{100}\)は31桁の整数です。



んー…まぁ確かに教科書にはこう書いてるんだけど…イマイチ意味がわかんないんだよね。
はい、ということで、少し詳しく見ていきましょう。
一番わかりやすいのは\(\log_{10}{2^{100}}=30.10\)を指数の形に戻す、
という操作かな、と思います。
\(\log_{10}{2^{100}}=30.10\)を対数の定義を使って指数の形に戻すと、
\(2^{100} = 10^{30.10}\)
\(\quad = 10^{30+0.10}=10^{0.10} \times 10^{30}\)
指数法則を使ってここまで変形することができました。\(10^{0.10}\)と\(10^{30}\)に分けたところがポイントです。



はぁ…\(2^{100}\)を\(10^{n}\)の形にするわけですね。\(10^{0.10}\)がよくわかんないですけど、なんとなくさっきの「大きい数や小さい数の表現方法」に似た形になってきましたね。
その通りです。実は\(10^{0.10} \times 10^{30}\)は、さっきやった「大きい数や小さい数の表現方法」なんですね。
ここで、\(10^{0.10}\)について考えていきます。
まず、 \(10^{r}\)の指数部分\(r\)が\(0 \leq r < 1\)の小数のとき、
\(10^0 = 1\)、\(10^1 = 10\)なので、
\(1 \leq 10^{r} < 10\)となります。
ですので、まさに、\(10^{0.10} \times 10^{30}\)は、\(1 \leq 10^{0.10} < 10\)なので
\( a \times 10^n\)
の形なんですね。
この形になれば、31桁の整数だ、というのもわかりやすいですし、この後応用問題でよく出る「最上位桁の数は?」の意味もわかりやすくなります。



では、\(1 \leq 10^{r} < 10\)について、徹底的に調べていきましょう!
\(\log_{10}{2} = 0.3010\)は今回の問題で与えられましたが、\(\log_{10}{1}\)〜\(\log_{10}{9}\)まで、全部調べていきます!
ちなみに、\(\log_{10}{3} = 0.4771\)と\(\log_{10}{7} =0.8451\)は常用対数表などで調べるしかないです。
ですが、後は\(\log_{10}{2}\)、\(\log_{10}{3}\)、\(\log_{10}{7}\)の値を使って計算できます。
では計算していきましょう!
- \(\log_{10}{1} = 0\)。これはいいですね。これも対数の定義を使って指数の形に戻しておきます。\(10^{0} = 1\)。
- \(\log_{10}{2} = 0.3010\)。これも指数の形にすると、\(10^{0.3010} = 2\)。
ここまでくると、ちょっと見えてきた人もいると思います。どんどんいきましょう!
- \(\log_{10}{3} = 0.4771 \leftrightarrow 10^{0.4771} = 3\)。
- \(\log_{10}{4} = \log_{10}{2^2}\)
\(\quad = 2\log_{10}{2} = 2 \times 0.3010 = 0.6020\)
\(\leftrightarrow 10^{0.6020} = 4\)。 - \(\displaystyle \log_{10}{5} = \log_{10}{\frac{10}{2}}\)
\(\quad =\log_{10}{10}-\log_{10}{2} = 1- 0.3010 = 0.6990\)
\(\leftrightarrow 10^{0.6990} = 5\)。(←ちなみにこの方法で\( \log_{10}{5}\)を計算する、というのはよくやります。覚えときましょう) - \(\displaystyle \log_{10}{6} = \log_{10}{2\times 3}\)
\(\quad =\log_{10}{2}+\log_{10}{3} = 0.3010 + 0.4771 = 0.7781\)
\(\leftrightarrow 10^{0.7781} = 6\)。 - \(\log_{10}{7} = 0.8451 \leftrightarrow 10^{0.8451} = 7\)。
- \(\log_{10}{8} = \log_{10}{2^3}\)
\(\quad = 3\log_{10}{2} = 3 \times 0.3010 = 0.9030\)
\(\leftrightarrow 10^{0.9030} = 8\)。 - \(\log_{10}{9} = \log_{10}{3^2}\)
\(\quad = 2\log_{10}{3} = 2 \times 0.4771 = 0.9542\)
\(\leftrightarrow 10^{0.9542} = 9\)。



一度、表にまとめておきましょう。
| \(1=10^{0}\) | \(6= 10^{0.7781}\) |
| \(2=10^{0.3010} \) | \(7=10^{0.8451}\) |
| \(3=10^{0.4771}\) | \(8= 10^{0.9030}\) |
| \(4 = 10^{0.6020}\) | \(9= 10^{0.9542}\) |
| \(5= 10^{0.6990}\) | \(10= 10^{1}\) |
ということで、\(10^r\)(ただし\(0 \leq r < 1\))の\(r\)の値を調べることで、\(10^r\)のおよその値を調べることができます!
ちなみに、\(2^{100}=10^{0.10} \times 10^{30}\)は31桁の数、というのもわかりますが、\(10^{0.10}\)は\(10^{0} < 10^{0.10} <10^{0.3010}\)、つまり
\(1 < 10^{0.10} <2\)
なので、最上位桁の数は1ということもわかります。



常用対数表を使えばもっと詳しく調べることができますよ!
| … | 5 | 6 | … | |
| … | ||||
| 1.2 | 0.0969 | 0.1004 | ||
| … |
大体、指数部分である\(0.10\)辺りを調べてみました。
常用対数表から、\(\log_{10}{1.25} = 0.0969\)、\(\log_{10}{1.26} = 0.1004\)なので、
\(10^{0.0969} = 1.25\)、\(10^{0.1004} = 1.26\)。
つまり、\(10^{0.0969} < 10^{0.10} < 10^{0.1004}\)。
よって、\(1.25 < 10^{0.10} < 1.26 \)なので、
\(2^{100}=1.25\cdots \times 10^{30}\)程度の値だ、ということまでわかりました。



常用対数を使えば、こうやって、大きな数や小さな数の大体の様子を調べることができるわけですね。
常用対数表も置いておきますので、よければ使ってください!
冒頭の借りたお金、いくら返す?
さて、では冒頭の話で太郎くんがいくら返さないといけないか、常用対数を使って計算してみましょう。



自分で自分の返済額計算するのって、なんかイヤだな…。
(解答)(←?)
まず、返済金額を立式してみましょう。
可哀想なことに、太郎くんはわけもわからず「複利計算」で借金をしてしまいました。
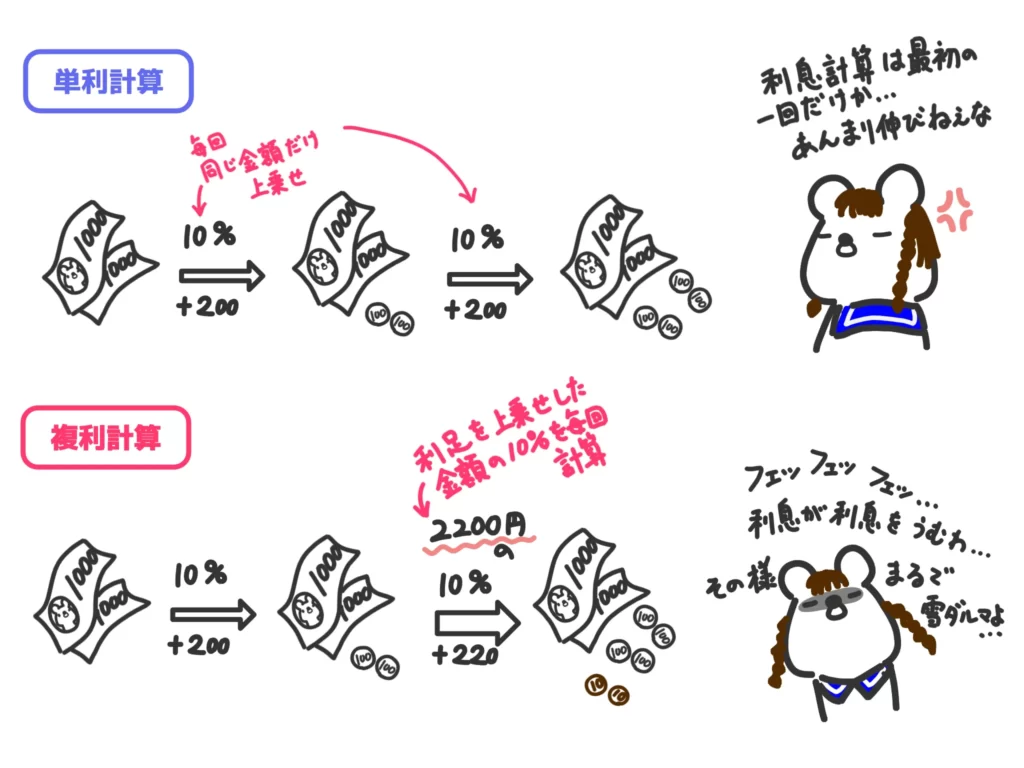

360日におまけしてくれたので、利息がつく回数は36回です。
ということで、
\(2000 \times 1.1 \times \cdots \times 1.1 = 2000(1.1)^{36}\)
となります。常用対数をとって計算すると、
\(\log_{10} \{ {2000(1.1)^{36}} \} = \log_{10} \{ {2 \times 10^3 \times (1.1)^{36}} \}\)
\(\quad = \log_{10}{2} + 3 \log_{10}{10} + 36 \log_{10}{1.1}\)
\(\quad = 0.3010 + 3 + 36 \times 0.0414 = 4.7914\)
指数の形に戻すと、\(2000(1.1)^{36} = 10^{4.7914} = 10^{0.7914}\times 10^4\)
再び常用対数表を使って指数部分である\(0.7914\)付近を調べます。
| … | 8 | 9 | |
| … | |||
| 6.1 | 0.7910 | 0.7917 | |
| … |
\(\log_{10}{6.18} = 0.7910\)、\(\log_{10}{6.19} = 0.7917\)なので、
\(10^{0.7910} = 6.18\)、\(10^{0.7917} = 6.19\)。
よって、\(6.18 < 10^{0.7914} < 6.19\)なので、
\(2000(1.1)^{36} = 6.18 \cdots \times 10^4 =\)約61800円
となります。



…。(え?借りたの2000円だったよね?なに?詐欺?詐欺にあったの?)



キリ良く62000円でいいわよ。



キリはよくなったけど、増えてる…。
実際に電卓を使って計算しても61825.3610…円、とかなり精度良く計算できているのがわかります。
※ トイチでお金を貸すのは法律違反です!良い子の皆はマネしない!
まとめ
ちょっとわかりにくい、常用対数について解説しました。
ポイントは、
- 大きい数、小さい数の表現方法を押さえる。
- 常用対数をとって計算した後、指数の形に戻す。
この2点です。



常用対数は大きい数や小さい数のおよその値を把握するために便利だ、というのも押さえておきましょう!