大数の法則と中心極限定理【わかりやすく雰囲気が伝わるように説明】

2023年8月17日

統計的な推測をする際に、全体（母集団）からサンプルをいくつか取ってきて（標本）、その特徴を調べる、という方法があります。

この記事では、標本の特徴を使って母集団を推測する際のベースになる、「大数の法則」と「中心極限定理」について説明していきます。

せんせ

今回は基本的な法則・定理の説明で、正直これを使ってどうこうする、ということはありません。
なので、茶番なしです。

大数の法則とは？

大数の法則

ざっくりと説明すると、標本の大きさ（サンプルサイズ。標本として取ってくる個数）が大きくなれば、母集団の特徴をより正確に推測できる、という法則です。

せんせ

標本の数を大きくしたり、試行回数を増やせば増やすほど、母集団の真の値や理論値に近づく、ということですね。
これは感覚的にわかりやすいと思います。

例えば、１つのサイコロを投げるとき、出る目の期待値は計算すれば\(\displaystyle 1 \cdot \frac{1}{6}+2 \cdot \frac{1}{6}+3 \cdot \frac{1}{6}+4 \cdot \frac{1}{6}+5 \cdot \frac{1}{6}+6 \cdot \frac{1}{6} = \frac{7}{2}\)ですが、

10回サイコロ投げをしたときの期待値（平均）より、1000回サイコロ投げをしたときの期待値（平均）の方が理論値\(\displaystyle \frac{7}{2}\)に近づく、

という話です。

たろぅ

そりゃそうだ。10回くらいなら運悪く出る目が偏るかもしれないけど、1000回もやればその偏りも少なくなるわな。

と思ってくれればOKです。

中心極限定理とは？

こっちはちょっとイメージしにくいかもしれません。

中心極限定理

こちらは母集団から標本を何度も取ることを前提としてイメージしています。

母集団から標本をとって、標本平均を計算する、という操作を何回か繰り返します。

すると、母集団がどんな形の分布でも（例外はあるけど、ほとんどの場合）、標本の大きさ（サンプルサイズ）が大きければ、標本平均の分布は母平均\(\mu\)に山をもつ正規分布に近づいていきます。しかも、標本の大きさが大きいほど、分布の幅は狭くなります（標本平均のばらつきが小さくなる）。

もう少し統計的に書くと、

母平均\(\mu\)、母分散\(\sigma^2\)である母集団（基本的に分布の形は問わない）から標本の大きさ\(n\)の標本を取って標本平均を計算すると、その標本平均は正規分布\(\displaystyle N \left( \mu ,\frac{\sigma ^2}{n} \right)\)に従います。

母集団がどんな分布だろうが、標本を取ってきて「標本平均」を計算するとその分布は正規分布になる、ということですね。「標本平均の分布」と言っているところがポイントです。

こちらは言っていることがわかりにくいのですが、状況の把握ができれば感覚的には理解することは難しくないはずです。

要は、「標本平均」に着目した場合、標本の大きさが大きければ（例えば標本を1000個ずつとってきて標本平均を計算すると）母平均あたりをとる可能性が高く、母平均から離れた値をとる可能性が低くなる、ということですね。

さらに、標本の大きさを大きくすればするほど、母集団を推測する精度が上がる（標本100個の平均より、標本1000個の平均の方が精度が高い）ので、標本平均は母平均あたりをとる可能性がさらに高くなり、母平均から離れる可能性はさらに低くなる。つまり分布の幅が狭くなる、ということになります。

せんせ

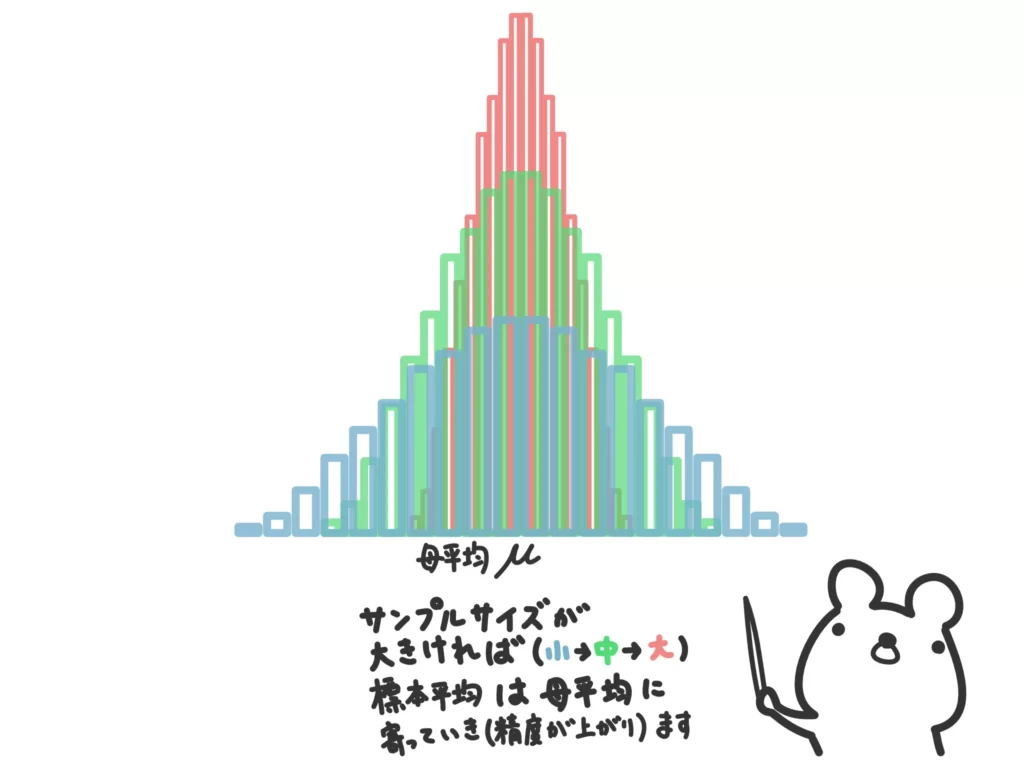
「標本平均の分布」、というのが最初は少しわかりにくいかもしれません。母集団の推測をする場合、偶然選んだその標本がどの程度正確なのか？というのが重要なので、例えば「標本平均の期待値がどの程度か？」や「標本平均がどんな分布に従うのか？」とかいう話になってきます。

まとめ

標本による推測の基本、大数の法則と中心極限定理についてでした。

とりあえずこれを使ってなにかする、ということはないのですが、標本を使った推定や検定をするときの元になる考え方ですので雰囲気だけでも押さえておきましょう。